The potential energy curves described above were used to compute relaxation and transfer cross sections. Fully quantal close-coupling studies of the neutral systems Na-H, Mg-H, Ca-H ans Sr-H were performed using the formulation given by Mies (1973) and generalized by Launay & Roueff (1977).
The radiating atom with angular momentum J collides with an H atom with angular momentum j2. We couple J and j2 to obtain the total angular momentum j of the two atoms. Owing to the invariance of the interaction potential V under rotations of the total system, the total angular momentum
![]() and its space fixed projection
and its space fixed projection ![]() are conserved during the collision. It is convenient to use scattering channel states
are conserved during the collision. It is convenient to use scattering channel states
![]() which describe the asymptotic fragments with relative angular momentum
which describe the asymptotic fragments with relative angular momentum
![]() .
The total wave function is expanded in terms of these channel states, the expansion coefficients are the radial amplitudes
.
The total wave function is expanded in terms of these channel states, the expansion coefficients are the radial amplitudes
![]() which satisfy the usual coupled
radial equations (Spielfiedel et al. 1991). This set of equations is always decoupled into two blocks as a result of parity conservation. In the calculations, we have assumed that the H atom remains in its ground 2S state
(L2=0,j2=1/2) and we have neglected collision-induced quenching to the other L states of the radiating atom. The scattering equations were solved subject to boundary conditions which define the T-matrix elements (Spielfiedel et al. 1991). The numerical method used is the Log Derivative Method (Johnson 1977).
Convergence was checked in terms of the range and step size in the scattering coordinate in the radial equations.
which satisfy the usual coupled
radial equations (Spielfiedel et al. 1991). This set of equations is always decoupled into two blocks as a result of parity conservation. In the calculations, we have assumed that the H atom remains in its ground 2S state
(L2=0,j2=1/2) and we have neglected collision-induced quenching to the other L states of the radiating atom. The scattering equations were solved subject to boundary conditions which define the T-matrix elements (Spielfiedel et al. 1991). The numerical method used is the Log Derivative Method (Johnson 1977).
Convergence was checked in terms of the range and step size in the scattering coordinate in the radial equations.
Under typical conditions of formation of strong resonance lines in stellar atmospheres, the interaction of the radiating atomic system with the perturbing gas is given by the relaxation matrix (Fano 1963). Under the assumption that the impact approximation is valid, the relaxation matrix ![]() is frequency independent and can be expressed in terms of collisional amplitudes (Nienhuis 1976) or collision T-matrix elements (Fano 1963). As the internal state distribution of the perturbers and the distribution of relative velocities are isotropic, the collisional relaxation of the atomic density matrix
is frequency independent and can be expressed in terms of collisional amplitudes (Nienhuis 1976) or collision T-matrix elements (Fano 1963). As the internal state distribution of the perturbers and the distribution of relative velocities are isotropic, the collisional relaxation of the atomic density matrix ![]() is fully isotropic. As a consequence, the relaxation matrix
is fully isotropic. As a consequence, the relaxation matrix ![]() is considerably simplified by using an expansion in components
is considerably simplified by using an expansion in components
![]() of irreductible tensorial sets (Fano 1949, 1954, 1957; Omont 1977; Blum 1981). We use here the same notations as in Paper I.
of irreductible tensorial sets (Fano 1949, 1954, 1957; Omont 1977; Blum 1981). We use here the same notations as in Paper I.
Due to the isotropy of the collisional relaxation, only the multipole components with the same value of ![]() and q are coupled, and the relaxation rate constants are q independent. Hence the relaxation equations may be written as:
and q are coupled, and the relaxation rate constants are q independent. Hence the relaxation equations may be written as:
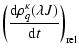 |
= | ||
| (1) |
For ![]() ,
,
![]() corresponds to collisional transfer of population
corresponds to collisional transfer of population
![]() ,
orientation
,
orientation
![]() and alignment
and alignment
![]() from state J' to state J.
from state J' to state J.
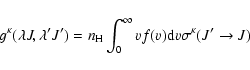 |
(2) |
| = | |||
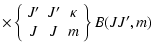 |
(3) |
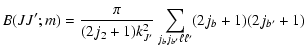 | |||
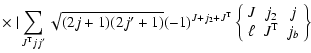 |
|||
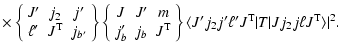 |
(4) | ||
For J= J':
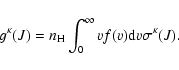 |
(5) |
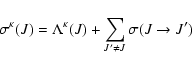 |
(6) |
![$\displaystyle \times \left \{\begin{array}{ccc}
m & J &J \\
\kappa &J &J \\
\end{array}\;\right\}]
B(JJ;m)$](/articles/aa/full/2002/29/aa2344/img75.gif) |
(7) |
| = | 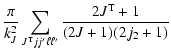 |
||
| (8) |
Copyright ESO 2002