

Up: Optimum imaging observation wavelength
Subsections
The effect of wavefront residual error of AOS on an optical image is to remove energy from
the central peak, distributing it into a surrounding halo. The halo is absent for a perfect wavefront,
but dominates the image structure in the presence of a wavefront error typical of uncompensated
turbulence.
For the astronomical telescope with AOS, the image resolution is most affected. To investigate
the image quality of AOS, it is useful to begin with the extended Marechal approximation, which
provides a relationship between the figure error and the Strehl ratio under weak-turbulence
conditions
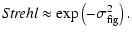 |
|
|
(20) |
This is only valid for small residual phase error. For most partial correction AOS, this condition is
generally not satisfied.
Assuming all of the energy lost from the central core of the beam is scattered over a region of
width
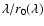 ,
a composite short-exposure image Strehl ratio (Parenti & Sasiela 1994) for partial correction AOS can be shown as
,
a composite short-exposure image Strehl ratio (Parenti & Sasiela 1994) for partial correction AOS can be shown as
![$\displaystyle {\it Strehl}_{\rm SE}\approx \exp\left(-\sigma_{\rm fig}^2\right)+\frac{1-\exp\left(-\sigma_{\rm fig}^2\right)}{1+[D/r_0(\lambda)]^2}\cdot$](/articles/aa/full/2002/29/aa1566/img73.gif) |
|
|
(21) |
Accordingly, the short-exposure image resolution (Parenti & Sasiela 1994) for partial
correction AOS can be expressed as
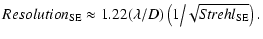 |
|
|
(22) |
Similarly, for the long-exposure imaging, the Strehl ratio and the resolution (Parenti & Sasiela
1994) for AOS can be approximated to
![$\displaystyle {\it Strehl}_{\rm LE}\approx\frac{\exp\left(-\sigma_{\rm fig}^2\r...
...rm tilt}^2}+\frac{1-\exp\left(-\sigma_{\rm fig}^2\right)}{1+[D/r_0(\lambda)]^2}$](/articles/aa/full/2002/29/aa1566/img75.gif) |
|
|
(23) |
and
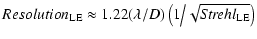 |
|
|
(24) |
respectively. Note that the first term of Eqs. (21) and (23) is the relative peak intensity of the
central core of the imaging beam and the second term is that of the surrounding halo. Generally,
the peak intensity of the central core is much larger than that of the halo for imaging with AOS.
As the figure residual error is very small, the short-exposure Strehl ratio can be simplified as
mentioned above. For partial correction adaptive optical systems, the imaging performance as
shown in Eqs. (21-24) is by far superior.
Figure 1 presents the short-exposure imaging resolution of AOS versus the observing
wavelength for different figure residual root mean square errors. It can be seen from Fig. 1 that
for a certain figure residual error, the imaging resolution improves with increasing observing
wavelength as the observing wavelength is relatively shorter. When the observing wavelength is
longer, the imaging performance gradually becomes worse with the lengthening of the wavelength.
Note that there exists an optimum observing wavelength in which the imaging resolution is
highest for a certain figure residual error. The larger the figure residual error, the longer the
optimum wavelength. So in astronomical telescopes with adaptive optics, the appropriate imaging
observation wavelength need to be selected based on the system capability and its mission in order
to exploit fully the compensation function of AOS for atmospheric turbulence.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa1566f1.eps}
\end{figure}](/articles/aa/full/2002/29/aa1566/Timg77.gif) |
Figure 1:
The imaging resolution vs. observing wavelength for adaptive optical systems. |
The optimum wavelength would maximize the imaging resolution of the astronomical
telescopes with adaptive optics. For convenience of analysis, a new function
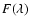 is defined to
used to optimize the imaging observation wavelength of AOS,
is defined to
used to optimize the imaging observation wavelength of AOS,
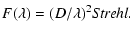 |
|
|
(25) |
Evidently, the maximizations of the function
 and the imaging resolution are both
equivalent.
and the imaging resolution are both
equivalent.
For short-exposure imaging, the imaging resolution depends mainly on the figure residual
error of AOS, so that
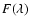 can be written as
can be written as
For astronomical imaging through adaptive optics correction for atmospheric turbulence, the
imaging Strehl ratio and the resolution mostly lies on the intensity distribution of the central core
of the beam. Note that generally the diameter of the system is much larger than the coherence
length, namely
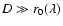 ,
so the function
,
so the function
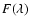 can be simplified as
can be simplified as
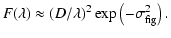 |
|
|
(27) |
Substituting Eqs. (16) into Eq. (27), one can obtain
![$\displaystyle F(\lambda)\approx(D/\lambda)^2\exp[-A(\lambda_0/\lambda)^2]$](/articles/aa/full/2002/29/aa1566/img85.gif) |
|
|
(28) |
where A is the figure residual error of AOS at the wavelength
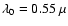 m,
m,
In order to verify the existence of the optimum imaging observation wavelength, one can
obtain, by taking the second order derivative for the function
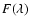 and letting it be less than
zero, the following inequation:
and letting it be less than
zero, the following inequation:
Solving the above inequation, one can obtain
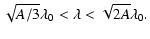 |
|
|
(31) |
That is to say that there exists an optimum imaging observation wavelength for AOS only as
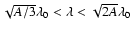 .
.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{aa1566f2.eps}
\end{figure}](/articles/aa/full/2002/29/aa1566/Timg94.gif) |
Figure 2:
Optimum short exposure observing wavelength and the corresponding image resolution. |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{aa1566f3.eps}
\end{figure}](/articles/aa/full/2002/29/aa1566/Timg95.gif) |
Figure 3:
Optimum long exposure observing wavelength and the corresponding image resolution. |
Taking the first order derivative for the function
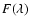 and letting it be equal to zero, we
can write:
and letting it be equal to zero, we
can write:
![$\displaystyle \frac{{\rm d}F(\lambda)}{{\rm d}\lambda}=\left(\frac{-2D^2}{\lamb...
...{2AD^2\lambda_0^2}{\lambda^5}\right)\exp\left[-A(\lambda_0/\lambda)^2\right]=0.$](/articles/aa/full/2002/29/aa1566/img96.gif) |
|
|
(32) |
For short-exposure imaging, the optimum imaging observation wavelength for AOS, taking
the solution of Eq. (32), can be derived as
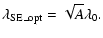 |
|
|
(33) |
According to Tyler (Tyler & Fender 1994), the optimal imaging observation wavelength for AOS
should be
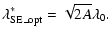 |
|
|
(34) |
Subsituting Eq. (33) into Eq. (22), the corresponding resolution for short-exposure
imaging at the optimum wavelength can be expressed approximately as
For long-exposure imaging, the imaging resolution depends not only on the figure residual
error but also on the tilt residual error of AOS, Thus
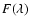 can be simplified as
can be simplified as
![$\displaystyle F(\lambda)\approx(D/\lambda)^2\frac{\exp[-A(\lambda_0/\lambda)^2]}{1+5B(\lambda_0/\lambda)^2}$](/articles/aa/full/2002/29/aa1566/img102.gif) |
|
|
(36) |
where B is the tilt residual error of AOS at the wavelength
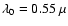 m,
m,
![$\displaystyle B=[f_{\rm T}(\lambda_0)/f_{\rm c}]^2+(\lambda_{\rm T}/\lambda_0)^2\pi f_{\rm c}\sigma_{\rm tn}^2/f_{\rm st}.$](/articles/aa/full/2002/29/aa1566/img103.gif) |
|
|
(37) |
Similarly, one can derive the optimum imaging observation wavelength for long-exposure
imaging as
![$\displaystyle \lambda_{\rm LE\_opt}=\left[\sqrt{\left(A+\sqrt{A^2+20AB}\right)\big/2}\right]\lambda_0.$](/articles/aa/full/2002/29/aa1566/img104.gif) |
|
|
(38) |
Subsituting Eq. (38) into Eq. (24), the corresponding resolution for long-exposure
imaging at the optimum wavelength can be expressed approximately as
Figures 2 and 3 present optimum imaging observation wavelength and the
corresponding image resolution for short-exposure imaging and long-exposure imaging
respectively. It can be seen from Figs. 2 and 3 that the optimum imaging observation
wavelength of AOS depends directly on the wavefront residual error of AOS. The larger the
wavefront residual error, the longer the optimum imaging observation wavelength is. Especially,
the optimum imaging observation wavelength for short-exposure imaging, see Eq. (33), can
be explained as the corresponding wavelength under the condition that the figure residual error is
1 rad2.
Furthermore, the optimal observing wavelength and the corresponding short-exposure
imaging resolution according to Tyler and Fender's (Tyler & Fender 1994) result, see Eq. (34), are also presented in Fig. 2. Note that the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994) is larger than that in this paper. The imaging performance according to
Tyler and Fender's result is inferior to the result of this paper. The interpretation is that the
imaging short-exposure Strehl ratio in Tyler and Fender's derivation (Tyler & Fender 1994) is approximated as
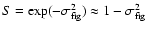 .
If the required precision is 10%, the figure residual
error should be less than 0.14 rad2. When the figure residual error is equal to 0.6 rad2, the precision
can only attain 27%. In contrast with the results of this paper, the percentages of the departure of
the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994) and the
corresponding imaging resolution are 41.4% and 10% respectively. Evidently, the imaging
resolution based on the calculated optimal observing wavelength in this paper is superior to that
according to the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994). This
result shows also that the calculation in this paper is more precise and more effective than the
rough estimate carried by Tyler and Fender (Tyler & Fender 1994).
.
If the required precision is 10%, the figure residual
error should be less than 0.14 rad2. When the figure residual error is equal to 0.6 rad2, the precision
can only attain 27%. In contrast with the results of this paper, the percentages of the departure of
the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994) and the
corresponding imaging resolution are 41.4% and 10% respectively. Evidently, the imaging
resolution based on the calculated optimal observing wavelength in this paper is superior to that
according to the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994). This
result shows also that the calculation in this paper is more precise and more effective than the
rough estimate carried by Tyler and Fender (Tyler & Fender 1994).
For nighttime astronomical telescopes with adaptive optics, the imaging observations are
mostly done at a range of wavelengths. Figure 4 presents the percentage of the short-exposure
imaging resolution departure from the optimum resolution as function of the percentage of the
observing wavelength departure from the optimum wavelength. As AOS is not operated in the
optimum wavelength but just 10% longer or shorter, the resolution degrades only about 1%. This
result shows that the derived optimum observing wavelength in this paper can be applied not only
in the monochromic observation with very narrow band but also in the nighttime observation with
a certain range of wavelength.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{aa1566f4.eps}
\end{figure}](/articles/aa/full/2002/29/aa1566/Timg112.gif) |
Figure 4:
The percentage of the short-exposure imaging resolution departure from the optimum resolution as a function of the percentage of the observing wavelength departure from the optimum wavelength. |


Up: Optimum imaging observation wavelength
Copyright ESO 2002
![]() ,
a composite short-exposure image Strehl ratio (Parenti & Sasiela 1994) for partial correction AOS can be shown as
,
a composite short-exposure image Strehl ratio (Parenti & Sasiela 1994) for partial correction AOS can be shown as
![$\displaystyle {\it Strehl}_{\rm SE}\approx \exp\left(-\sigma_{\rm fig}^2\right)+\frac{1-\exp\left(-\sigma_{\rm fig}^2\right)}{1+[D/r_0(\lambda)]^2}\cdot$](/articles/aa/full/2002/29/aa1566/img73.gif)
![$\displaystyle {\it Strehl}_{\rm LE}\approx\frac{\exp\left(-\sigma_{\rm fig}^2\r...
...rm tilt}^2}+\frac{1-\exp\left(-\sigma_{\rm fig}^2\right)}{1+[D/r_0(\lambda)]^2}$](/articles/aa/full/2002/29/aa1566/img75.gif)
![]() is defined to
used to optimize the imaging observation wavelength of AOS,
is defined to
used to optimize the imaging observation wavelength of AOS,
![]() can be written as
can be written as
![$\displaystyle (D/\lambda)^2
\left[\exp\left(-\sigma_{\rm fig}^2\right)+\frac{1-\exp\left(-\sigma_{\rm fig}^2\right)}{1+\left(D/r_0(\lambda)\right)^2}\right]\cdot$](/articles/aa/full/2002/29/aa1566/img82.gif)
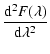 =
=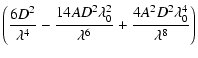
![]() and letting it be equal to zero, we
can write:
and letting it be equal to zero, we
can write:
![$\displaystyle \frac{{\rm d}F(\lambda)}{{\rm d}\lambda}=\left(\frac{-2D^2}{\lamb...
...{2AD^2\lambda_0^2}{\lambda^5}\right)\exp\left[-A(\lambda_0/\lambda)^2\right]=0.$](/articles/aa/full/2002/29/aa1566/img96.gif)
![]() can be simplified as
can be simplified as
![$\displaystyle F(\lambda)\approx(D/\lambda)^2\frac{\exp[-A(\lambda_0/\lambda)^2]}{1+5B(\lambda_0/\lambda)^2}$](/articles/aa/full/2002/29/aa1566/img102.gif)
![$\displaystyle \lambda_{\rm LE\_opt}=\left[\sqrt{\left(A+\sqrt{A^2+20AB}\right)\big/2}\right]\lambda_0.$](/articles/aa/full/2002/29/aa1566/img104.gif)
![$\displaystyle 1.22\Bigg\{\left[\left(A+\sqrt{A^2+20AB}\right)+10B\right]$](/articles/aa/full/2002/29/aa1566/img108.gif)
![$\displaystyle \times\frac{\exp\left[2\big/\left(1+\sqrt{1+20B/A}\right)\right]}{A+\sqrt{A^2+20AB}}\Bigg\}$](/articles/aa/full/2002/29/aa1566/img109.gif)
![]() .
If the required precision is 10%, the figure residual
error should be less than 0.14 rad2. When the figure residual error is equal to 0.6 rad2, the precision
can only attain 27%. In contrast with the results of this paper, the percentages of the departure of
the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994) and the
corresponding imaging resolution are 41.4% and 10% respectively. Evidently, the imaging
resolution based on the calculated optimal observing wavelength in this paper is superior to that
according to the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994). This
result shows also that the calculation in this paper is more precise and more effective than the
rough estimate carried by Tyler and Fender (Tyler & Fender 1994).
.
If the required precision is 10%, the figure residual
error should be less than 0.14 rad2. When the figure residual error is equal to 0.6 rad2, the precision
can only attain 27%. In contrast with the results of this paper, the percentages of the departure of
the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994) and the
corresponding imaging resolution are 41.4% and 10% respectively. Evidently, the imaging
resolution based on the calculated optimal observing wavelength in this paper is superior to that
according to the optimal wavelength derived by Tyler and Fender (Tyler & Fender 1994). This
result shows also that the calculation in this paper is more precise and more effective than the
rough estimate carried by Tyler and Fender (Tyler & Fender 1994).