Most adaptive optics compensation systems apply the conjugate surface of the phase measured by WFS with a pair of active elements consisting of a high-speed TM and a DM. TM is usually used to correct the tilt component of the wavefront distortions induced by atmospheric turbulence. The figure (tilt-removed) component of the wavefront perturbation is compensated by DM. In the practical AOS, the compensation is not perfect because of the individual errors such as the uncompensated turbulence-induced error due to the finite bandwidth of the servo system and the measurement noise.
The main figure residual errors include: (1) uncompensated turbulence-induced figure error due to the bandwidth of the figure compensation servo system; (2) closed-loop figure noise error due to the measurement error of the wavefront sensor; (3) fitting error due to the finite corrector elements; (4) anisoplanatic error due to the angular anisoplanatism and the focal anisoplanatism.
The uncompensated turbulence-induced figure error depends on the temporal power spectrum
of the figure (tilt-removed) component of the turbulence
![]() and the servo control transfer function
and the servo control transfer function
![]() :
:
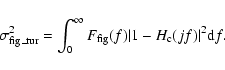 |
(5) |
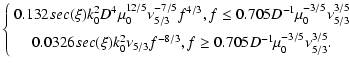 |
(6) |
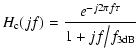 |
(7) |
For high-bandwidth figure compensation, the uncompensated turbulence-induced figure error
at the imaging wavelength ![]() can be obtained with the high-frequency form of the figure
spectrum over the entire frequency range, so that (Li et al. 2000):
can be obtained with the high-frequency form of the figure
spectrum over the entire frequency range, so that (Li et al. 2000):
| = | |||
| (8) |
In AOS, the noise resulting from WFS mainly consists of the photon shot noise due to the
finite light intensity and the read-out noise of the detector such as a CCD. Assuming the noise is
white, the closed-loop figure noise error can be obtained as (Rao et al. 2000):
| = | 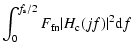 |
||
| = | (9) |
Note that the wavefront measurement noise
![]() relates the noise power spectrum to:
relates the noise power spectrum to:
| (10) |
| (11) |
The uncorrected phase error due to the figure (tilt-removed) component of turbulence at the
imaging wavelength ![]() ,
namely figure fitting error, is conveniently expressed in terms of the ratio of the subaperture spacing and the turbulence coherence length (Hardy 1998):
,
namely figure fitting error, is conveniently expressed in terms of the ratio of the subaperture spacing and the turbulence coherence length (Hardy 1998):
| (12) |
When the beacon of AOS and the target object do not lie in the same direction, the error due
to angular anisoplanatism at the imaging wavelength ![]() can be expressed as (Fried 1982)
can be expressed as (Fried 1982)
| (13) |
Furthermore, because the atmospheric turbulence is only partially detected by the beacon
light, the use of laser beacons in AOS produces the error due to focal anisoplanatism, which may
be expressed as (Tyler 1994)
| (14) |
| = | |||
| (15) |
The total figure residual error of AOS with the unit of phase rad2 at the imaging wavelength ![]() may be expressed as the sum of individual errors in the form
may be expressed as the sum of individual errors in the form
| = | |||
| = | |||
| (16) |
In AOS, the tilt component of turbulence is often measure by quadrant detectors and centroid trackers. This tilt belongs to G-tilt, namely average gradient over the pupil. The main errors involved in compensating the tilt component of turbulence are: (1) uncompensated turbulence-induced tilt error due to the bandwidth of the tilt compensation servo system; (2) closed-loop tilt noise error due to the measurement error of the tracking sensor.
According to the tracking frequency ![]() defined by Tyler (Tyler 1994), see Eq. (4), the uncompensated turbulence-induced tilt error at the imaging wavelength
defined by Tyler (Tyler 1994), see Eq. (4), the uncompensated turbulence-induced tilt error at the imaging wavelength ![]() can be expressed as
can be expressed as
| (17) |
Similar to the closed-loop figure noise error, the closed-loop tilt noise error at the imaging
wavelength ![]() relates the tilt measurement error
relates the tilt measurement error
![]() ,
the sampling frequency of the tracking system
,
the sampling frequency of the tracking system
![]() and the closed-loop -3dB bandwidth of the tracking servo loop to
and the closed-loop -3dB bandwidth of the tracking servo loop to
| (18) |
The total tilt residual error with the unit of tilt rad2 at the imaging wavelength ![]() is given by the sum of the uncompensated turbulence-induced tilt error and the closed-loop tilt noise error,
is given by the sum of the uncompensated turbulence-induced tilt error and the closed-loop tilt noise error,
| = | |||
| = | (19) |
Copyright ESO 2002