The absolute zero point of the radial-velocity measures, which is effectively set by the long-term drift corrections described in Sect. 5.5, rests on the assumptions (1) that the integrated solar disk spectrum has no significant long-term velocity variation; (2) that the ELODIE instrument has sufficient long-term stability; (3) that the wavelength scale in the Solar Flux Atlas correctly represents the measurements of an observer in circular orbit at 1 AU distance from the Sun; and (4) that the laboratory wavelengths, in this case for the Fe I lines, have no zero point error. Below, we discuss each of these assumptions.
The long-term wavelength stability of line shifts and asymmetries in the solar
spectrum has been the subject of several investigations. Concerning line shifts,
McMillan et al. (1993) found an upper limit of 
m s-1 for the variation
of ultraviolet
absorption lines over a solar cycle; while Deming & Plymate (1994) found an amplitude
of 10-15 m s-1 in the infrared. The continuous low-frequency velocity
spectrum was measured e.g. by Pallé et al. (1995), who found a mean spectral
density <
m2 s-2 Hz-1 for frequencies below 10-5 Hz,
i.e. on time scales longer than 
1 day. For daily averages, this implies
an amplitude less than a few m s-1. Livingston et al. (1999) followed the
full-disk asymmetries of Fe I lines for more than a solar cycle and
found cyclic variations in the line asymmetry with an amplitude of about
20 m s-1; presumably the corresponding absolute shifts are at least
of a similar size. Variations of the order 20-30 m s-1 are also
predicted from spatially resolved observations in active regions
(e.g. Brandt & Solanki 1990; Spruit et al. 1990) combined with the known long-term variations
in their fractional coverage of the solar disk (e.g. Tang et al. 1984).
For a general discussion of solar-cycle variations, see also Dravins (1999).
Thus, although direct observations are inconclusive, there are good reasons
to expect long-term variations of the visual solar line shifts of the order
30 m s-1. The results of Livingston et al. (1999) suggest that such changes
may occur on time scales of a year or less. We cannot therefore rule out
that the solar spectrum changed significantly between February and October
1997, although instrumental effects remain a more likely explanation for the
systematic difference of 
100 m s-1 between the two observation
sessions, as assumed in Sect. 5.5.
In a general sense, the ELODIE instrument has a proven long-term
stability, which may be better than 10 m s-1 (Udry et al. 1999). However,
the instrument was here used in a non-standard mode with time-separated
Th-Ar exposures and with the Moon spectrum as an intermediate reference.
The use of an extended source like the Moon for wavelength calibration is
traditionally frown upon (see, e.g., Sect. VIIb in Griffin et al. 1988), but
the use of fibre-fed échelle spectrometers has probably eliminated much
of that problem (Baranne 1999). Even so, the systematic difference of
39 m s-1 between the February and October results for the Moon
(Table 1) indicates some additional effect in our data.
The behaviour of 
versus the FWHM of the synthetic template is
very different in the two observation sessions, which leads us to believe
that the systematic difference could be explained by a slight change in the
asymmetry of the instrument profile, perhaps due to some readjustment of
the spectrometer in the intervening period. In view of such results we estimate
that the instrumental contributions to the standard error of the zero point
are of the order 50 m s-1.
The Solar Flux Atlas from 296 to 1300 nm by Kurucz et al. (1984) is a spectrum of the disk-integrated sunlight obtained with a FTS yielding a spectral resolution ranging from 348 000 in ultraviolet to 522 000 in red and infrared, and with S/N up to 9000. The wavelength scale has been corrected for Sun-Earth velocity shifts, but the gravitational redshift relative to a terrestrial observer (633.5 m s-1) was not removed, nor, presumably, the transverse Doppler shift from the Earth's orbital motion (1.5 m s-1). Each scan of the FTS covering a certain spectral region provided an intrinsically uniform wavelength scale, but a multiplicative factor had to be determined by means of the telluric O2line at 688.38335 nm. As this was only observed in some scans, the resulting scale was transferred to the other scans by matching overlapping parts of the spectra. As a result of this fitting and shifting, Kurucz et al. consider that the final wavelengths may have errors up to 100 m s -1, especially in the ultraviolet end. Allende Prieto & García López (1998b) examined the absolute wavelength calibration of the Solar Flux Atlas by computing the shifts for the minima of 1446 Fe I lines. They found that lines with equivalent widths >20 pm have a mean shift within 20 m s-1 of the value expected from non-kinematic effects (632.0 m s-1), with a scatter of 58 m s-1. Moreover, there is no visible trend with wavelength. From this we conclude that the wavelength scale of the Atlas is probably at least as good as claimed by its authors, i.e. with a zero point error less than 100 m s-1. Thanks to the expected wavelength coherency within each scan of the Atlas it may be possible to improve this zero point a posteriori.
Concerning the accuracy of the laboratory wavelengths, Nave et al. (1994)
quote systematic errors of the order 0.001 cm-1 due to the calibration
error for each laboratory spectrum, and possible pressure or current-dependent
shifts estimated to be less than 0.001 cm-1 (=15 m s-1 at
nm) for lines with upper levels of low excitation (<6 eV).
Since a majority of the lines used to construct our Fe I template
have excitation levels below 6.5 eV we estimate that the total systematic
error due to these factors is less than 30 m s-1.
Combining the various estimated contributions to the zero point error (Table 3), we find that the total uncertainty is of the order 120 m s-1. The main uncertainty comes from the wavelength scale of the Solar Flux Atlas. If that could be improved, as suggested above, it would immediately result in much more accurate radial-velocity measures for all the stars in Table 2, via a simple zero-point correction.
 |
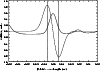Figure 6:
Illustration of the effective weighting function for the cross-correlation method
used in this paper. The thick curve is an inverted portion of the disk-integrated
solar spectrum (Kurucz et al. 1984) centred on the Fe I line at 522.55327 nm.
The weighting function, shown by the thin curve, is the derivative of a Gaussian
with
 km s-1. The centre of the spectral line is determined
by nulling the cross-correlation of the two functions. The weighting function
thus defines which parts of the spectral line are used to derive its shift. |
The radial-velocity measure refers to specific features in the observed stellar spectrum, and may well be different for different atomic species, or depending on which parts of the spectral lines are used. When publishing radial-velocity measures purporting to be accurate at the 100 m s-1level, it is necessary to specify, as well as possible, to which spectral features they refer. The selection of spectral lines is in our case given by the list of Fe I lines used to build the synthetic template. This list is available on request from the authors.
Given that all stellar absorption lines are in reality asymmetric, the
way to determine their centres is also of primary concern. The line centres
are implicitly defined by the cross-correlation method in combination with
the instrument. To see how this works, consider
that the true stellar spectrum is smeared first by the instrumental profile
(having a FWHM of 7.2 km s-1; Baranne et al. 1996) and then,
in the cross-correlation, by the template profile (which in our case is
Gaussian with
km s-1). The combined profile (p) is
approximately Gaussian with
km s-1. It is mainly this
combined profile that defines the centroid position with respect to the
true stellar spectrum. In maximising the CCF, the relative weights assigned
to the different parts of a spectral line are given by the derivative
p' (Fig. 6). This "weighting function'' (Lindegren 1978) has its
extreme points at 
km s-1 (at the dotted lines in the figure),
and it is roughly these two points in the absorption line that are balanced
against each other. Depending on the actual width of the stellar line, this
may happen deep in the line (e.g. for a rotationally broadened spectrum) or
nearer the continuum (for a sharp-lined spectrum).
Our procedure is intended to yield radial-velocity measures that are accurate (or absolute) in the sense that successive improvements of the technique should yield results that approach the true values. In practice it means that the values should be reproducible with other instruments and procedures having similar aims. Thus, as discussed above, special care was taken to ensure that the results refer to an absolute wavelength scale and to known and well-defined features in the stellar spectra, through procedures that might be repeated on another instrument.
Much effort in recent radial-velocity work has focused on achieving the very high precisions required to search for exoplanets. Such techniques, which aim at detecting small changes in the velocity but where the zero point is of little interest, could properly be called accelerometry (Connes 1985). The very high stability of instruments such as ELODIE is a direct consequence of such efforts. While our results benefit much from this stability, our goal is rather different from accelerometry, and many of the techniques developed for that purpose are not applicable here.
In fact, to achieve high accuracy usually means that some precision must be sacrificed. This may at first seem paradoxical, since accuracy implies precision (but not vice versa). However, it is a practical consequence of the limited signal-to-noise ratio in available data. Two circumstances can serve to illustrate this.
Firstly, to derive absolute line shifts obviously requires that only spectral lines with accurate laboratory wavelengths can be used. At accuracy levels below 100 m s-1 this very severely limits the number of available lines. This would not be a problem if each line could be measured with infinite signal-to-noise ratio, but in a real situation it means that precision is reduced compared to using all measurable lines in the stellar spectrum.
Secondly, as pointed out by Butler et al. (1996), a truly photon-noise limited Doppler analysis must consist of a full model of the spectroscopic observation. This can be achieved by fitting a model spectrum, affected by all the instrumental effects, to the observed data, using the appropriate statistical weighting of each pixel. In practice, the most precise model spectrum available for any given star is simply the mean observed spectrum of that star, recorded with the same instrument setup. This would allow to measure the relative shifts of the individual spectra with optimal precision, but not at all accurate.
Thus, a proper balance between accuracy and precision must in practice be found, depending on the application. In accelerometry, the emphasis is entirely on precision. In our case, where an ultimate goal is to derive intrinsic stellar parameters through comparison with astrometric radial velocities, the balance is instead shifted towards accuracy. A practical consequence is that our method would be suboptimal for accelerometry.
Copyright ESO 2002