![\begin{displaymath}% latex2html id marker 231
\includegraphics[width=5cm,clip]{equation1.ps}\end{displaymath}](/articles/aa/full/2002/28/aah2983/img10.gif) |
(1) |
The oxidation of carbon particles is a process which has extensively been studied in the laboratory. In Duschl et al. (1996) and Finocchi et al. (1997a) the results for the basic oxidation mechanism of solid carbon obtained in the chemistry of flames are applied to the problem of destruction of carbon dust grains in protoplanetary accretion discs. Under conditions encountered in the early Solar Nebula the basic reaction scheme for oxidation of solid carbon into CO starts with the reaction
where a OH radical attacks a six-ring at the periphery of a large PAH and cracks
carbon-carbon bonds. The rate for this starter reaction is
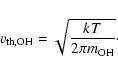 |
(3) |
The details of the calculation of the rate
![]() for an ensemble of
carbon grains with different radii are described in Paper I.
for an ensemble of
carbon grains with different radii are described in Paper I.
The next step in the reaction sequence is (El-Gamal 1995)
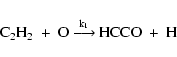 |
(5) |
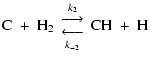 |
(9) | ||
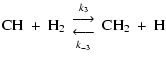 |
(10) | ||
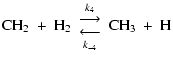 |
(11) | ||
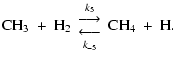 |
(12) |
The carbon dust oxidation reaction (1) leads to production
of CO molecules in the reaction step (4) and to the buildup
of a population of hydrocarbon molecules CHn (![]() ), most of which are
in the form of CH4. The main loss process for this group of molecules is
the reaction between two CH3 molecules
), most of which are
in the form of CH4. The main loss process for this group of molecules is
the reaction between two CH3 molecules
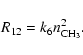 |
(19) |
Reactions between two CH3 molecules also result in the formation of C2H5 and C2H6, but this is followed by reactions finally leading back to CH3. This side-chain of reactions is considered separately.
The ethylene formed by reaction (18) is in equilibrium with
C2H3 by means of the fast exchange reaction
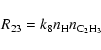 |
(22) |
| (23) |
The main loss process for this group of hydrocarbons are the oxidation reactions
| (30) |
The conversion of the two carbon atoms liberated by the starter reaction (1) into CO occurs in two steps. The first CO molecule is formed at once by reaction (4), the rate term R01 in (33) corresponds to this process, while the second CO molecule is formed by the sequence of reactions just described, the rate term R34 in (33) corresponds to this second process. The formation of the second CO molecule occurs via a cyclic process, by which one CH3 molecule acts as a catalyst which undergoes a sequence of reactions, starting by reacting with a second CH3 molecule, until finally one CH3 molecule is converted into CO while the other CH3 molecule is recovered. Figure 1 schematically shows this reaction cycle.
Besides these reactions, a number of less efficient side-reactions of the reaction chain leading to CO and other hydrocarbons are active. Some of them are discussed in Finocchi et al. (1997a). These reaction path's are not included in the present model calculation. We consider only the main route to CO which accounts for the dominating part of the CO formation rate. More detailed calculations based on a big reaction network are given in Finocchi & Gail (1997b), but the results for CO production based on the extended reaction network are not significantly different from what one obtains from the present reduced set of reaction equations.
The equation for CO formation by carbon combustion is
For computational purposes we found it to be advantageous to combine the set of
equations into a few groups. We define
| n0 | = | (34) | |
| n1 | = | (35) | |
| n2 | = | (36) | |
| n3 | = | (37) |
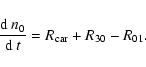 |
(38) |
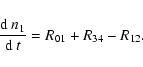 |
(39) |
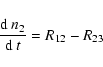 |
(40) |
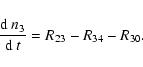 |
(41) |
Within each of the groups 1, 2, and 3 the relative abundance of the group
members is determined by the fast exchange reactions with H and H2. The
reactions for transition from one group to the next are much slower (cf. Fig. 3 or Tables 3 and 4 in Finocchi et al. 1997a). For determining the relative abundances within the groups we may use the
stationary equations with the intergroup transition terms neglected and solve
for the individual particle densities in terms of the group densities. We obtain
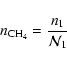 |
(42) |
![$\displaystyle %
{\cal N}_1=
\left[
1+{k_{-5}n_{\rm H}\over k_5n_{\rm H_2}}
\lef...
...t(
1+{k_{-2}n_{\rm H}\over k_2n_{\rm H_2}}
\right)
\right)
\right)
\right]\cdot$](/articles/aa/full/2002/28/aah2983/img66.gif) |
(43) |
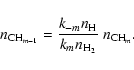 |
(44) |
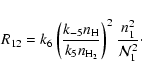 |
(45) |
For the second group we obtain
| |
= | 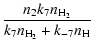 |
(46) |
| = | (47) |
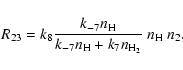 |
(48) |
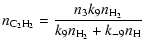 |
(49) | ||
| (50) |
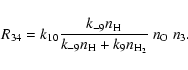 |
(51) |
CO is the dominating carbon-oxygen compound at high temperatures in the inner
disc regions. Also at very low temperatures the carbon not bound in carbon
grains is mainly bound in CO, other carbon bearing species having only very low
abundances in the outer part of the protoplanetary disc, provided the
composition in that region equals that of the parent molecular cloud. At medium
temperatures, however, if it is assumed that conversion to CH4 is kinetically
forbidden (e.g. Fegley & Prinn 1989), most of the CO will be converted
into CO2. The most efficient reaction for the interconversion of CO and
CO2 is
The formation of C2H5 and of ethane is possible by a side chain of the
main reaction route from carbon dust to CO and CO2 considered up to
now. These molecules may be formed by the following reactions
| Rate | A | Ea/k | Source | |
|
|
[K] | |||
| k0 |
|
0 | 16 100 | 1 |
| k1 |
|
2.10 | 790 | 3 |
| k2 |
|
0 | 11 700 | 2 |
| k3 |
|
0 | 1760 | 3 |
| k4 |
|
0 | 0 | 3 |
| k5 |
|
2.74 | 4740 | 3 |
| k6 |
|
0 | 16 500 | 2,1 |
| k7 |
|
0 | 0 | 1 |
| k8 |
|
0 | 0 | 3 |
| k9 |
|
0 | 14 000 | 3 |
| k10 |
|
2.10 | 790 | 3 |
| k11 |
|
0 | 0 | 3 |
| k-12 |
|
0.50 | 7550 | 2 |
| k13 |
|
1.50 | 250 | 3 |
| k14 |
|
0 | 6800 | 3 |
| k-14 |
|
0 | 0 | 3 |
| k15 |
|
3.60 | 4250 | 3 |
| k-15 |
|
1.50 | 3370 | 3 |
| k17 |
|
1.00 | 22 640 | 4 |
| k18 |
|
0 | 7800 | 1 |
|
Sources: (1): El-Gamal (1995), (2): UMIST data-file (Millar et al. 1997), (3): Baulch et al. (1994), (4) NIST. |
According to observations of cometary nuclei, methanol is a very abundant
component in the ice mixture of comets. For this reason we include in our
calculation of the chemistry as a test case the reactions for the formation of
CH3OH by
The rate coefficients are approximated in the standard Arrhenius form
| (62) |
The rate coefficients for the reverse reactions are calculated by means of the
principle of detailed balancing from rate coefficients of the forward reactions
and the mass action constant for the reaction in chemical equilibrium. The mass
action constants are calculated from thermodynamical data given in Barin
(1995). The free enthalpy of formation of molecules from the free
atoms is fitted by the following expression
| Molecule | a | b | c | d | e |
| H2 |
|
|
|
|
|
| CH |
|
|
|
|
|
| CH2 |
|
|
|
|
|
| CH3 |
|
|
|
|
|
| CH4 |
|
|
|
|
|
| C2 |
|
|
|
|
|
| C2H |
|
|
|
|
|
| C2H2 |
|
|
|
|
|
| C2H3 |
|
|
|
|
|
| C2H4 |
|
|
|
|
|
| C2H5 |
|
|
|
|
|
| C2H6 |
|
|
|
|
|
| OH |
|
|
|
|
|
| H2O |
|
|
|
|
|
| CO |
|
|
|
|
|
| CO2 |
|
|
|
|
|
| CH3O |
|
|
|
|
|
| CH3OH |
|
|
|
|
|
Copyright ESO 2002