The calculation of the radial mixing in the disc and of the chemical reactions of the carbon oxidation products in the gas phase requires to calculate a self consistent model for the accretion disc including the chemistry since this determines some important input parameters for the calculation of the chemistry, the temperature for instance, which depend itself on the chemistry in the disc. This calculation follows essentially the lines described in Paper I. There is only one modification compared to that paper that now pyroxene is considered as a separate dust component. This, however, does not result in significant changes of the model structure as described in Paper I.
Models are calculated for a protostellar accretion disc around a single star
with the set of parameters shown in Table 3. The model is
a stationary one-zone Keplerian ![]() -disc model. The stellar
parameters correspond to a star of one solar mass in a stage of evolution where
the star is already visible, i.e. the process of mass infall and star
formation is nearly finished and the remaining disc gradually disappears by
accretion onto the star (cf. Stahler & Walter 1993). This is just
that phase of the disc evolution which we want to consider. The viscosity
parameter
-disc model. The stellar
parameters correspond to a star of one solar mass in a stage of evolution where
the star is already visible, i.e. the process of mass infall and star
formation is nearly finished and the remaining disc gradually disappears by
accretion onto the star (cf. Stahler & Walter 1993). This is just
that phase of the disc evolution which we want to consider. The viscosity
parameter ![]() is set to a value which results in a timescale for disc
disappearance in time dependent one-zone model calculations which is of the
order of the observed timescale of roughly 107 years (Ruden & Pollack
1991). Slightly higher values for
is set to a value which results in a timescale for disc
disappearance in time dependent one-zone model calculations which is of the
order of the observed timescale of roughly 107 years (Ruden & Pollack
1991). Slightly higher values for ![]() are favoured by others
(e.g. Lin & Papaloizou 1996; Stepinski 1998).
are favoured by others
(e.g. Lin & Papaloizou 1996; Stepinski 1998).
The calculation is done for a mass accretion rate of
![]() .
This rate is suggested by typical disk masses of 0.1
.
This rate is suggested by typical disk masses of 0.1 ![]() around solar mass stars and typical disc lifetimes of 106 years (e.g.
Beckwith & Sargent 1993). This accretion rate is generally thought to
be representative for the early stages of the evolution of a protoplanetary
disc prior to the onset of planetary formation. For comparison also models
with an accretion rate of 10-6 and
around solar mass stars and typical disc lifetimes of 106 years (e.g.
Beckwith & Sargent 1993). This accretion rate is generally thought to
be representative for the early stages of the evolution of a protoplanetary
disc prior to the onset of planetary formation. For comparison also models
with an accretion rate of 10-6 and
![]() are
calculated. The former corresponds to an early evolutionary stage where the
parent molecular cloud is not yet dissipated and the system is hidden behind a
thick dust shell. The latter mass accretion rate probably corresponds to a
late stage of the disc evolution where planet formation already is underway.
Observationally determined mass accretion rates for young stellar objects of
age less than 106 yr seem to support our assumption of a mass
accretion rate of
are
calculated. The former corresponds to an early evolutionary stage where the
parent molecular cloud is not yet dissipated and the system is hidden behind a
thick dust shell. The latter mass accretion rate probably corresponds to a
late stage of the disc evolution where planet formation already is underway.
Observationally determined mass accretion rates for young stellar objects of
age less than 106 yr seem to support our assumption of a mass
accretion rate of
![]() for the pre-planet-formation
phase though the scattering of observationally determined accretion rates
is large (e.g. Hartmann 2000; Calvet et al. 2000).
for the pre-planet-formation
phase though the scattering of observationally determined accretion rates
is large (e.g. Hartmann 2000; Calvet et al. 2000).
In order to achieve a good radial resolution of the model and a good accuracy of the solution of the diffusion equations a fine grid of 200 radial grid points per decade is used. A control calculation with a finer resolution of 1000 grid-points per decade yielded nearly identical results.
The main purpose of this paper is to determine the radial variation of the concentration of hydrocarbons within the disc which are formed at about 0.5 AU by oxidation of carbon grains. We have solved the coupled system of stationary transport-diffusion-reaction equations for the groups n0, n1, n2, and n3 defined in Sect. 2.3 and determined from this the abundance of the individual molecules. Because stationarity is assumed the results of the present model calculation can only be applied for the inner disc region up to at most 30 AU since only in this part of the disc after about 106 years stationary conditions are reached (e.g. Ruden & Lin 1986; Wehrstedt & Gail 2002). Also the results of the present calculation cannot be applied to processes occuring after about 106 years because then most likely gaps are formed in the disc after the onset of formation of the big planets. This most likely makes any further mixing from the innermost disc regions into the outer parts of the disc impossible.
In calculating the abundances of molecules of the different groups defined in
Sect. 2.3 we assumed that the intra-group reaction timescales
are much shorter than the inter-group reaction timescales. This requires a
check. Figure 3 shows characteristic timescales for some of
the important reactions, defined as
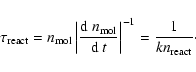 |
(69) |
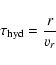 |
(70) |
The condensation reaction (18) to form C2H4 from CH3and the reaction (28) for the final formation of a CO molecule are clearly much slower than all other reactions. The intra-group reactions timescales are faster than the characteristic loss timescales of each group, such that within each of the groups the group members are in an equilibrium state with respect to the hydrogen abstraction and addition reactions. This justifies our procedure to collect all molecules into groups which are linked by the fast hydrogen abstraction and addition reactions and to consider the reaction kinetics only for groups and not for individual molecules.
Figure 3 also shows that for the model with
![]() the chemical reactions proceed in the warm inner part of
the disc (
the chemical reactions proceed in the warm inner part of
the disc (
![]() AU) on a much shorter timescale than the hydrodynamic
timescale. The chemistry in this region, thus, is in a nearly stationary state,
except for the slow formation of CO. From Fig. 3 one also
infers that the conversion of hydrocarbons into CO ceases if matter is mixed
from the inner disc region
AU) on a much shorter timescale than the hydrodynamic
timescale. The chemistry in this region, thus, is in a nearly stationary state,
except for the slow formation of CO. From Fig. 3 one also
infers that the conversion of hydrocarbons into CO ceases if matter is mixed
from the inner disc region
![]() AU into the region
AU into the region
![]() AU.
AU.
Figure 4 shows the radial variation of the concentration of
particles from groups 0, ... 3 as defined in Sect. 2.3, and
the concentration of CO and CO2 molecules. Only the group n1 of CHn(![]() )
molecules and the group n3 of C2H2 and C2H have
significant abundances. The high abundance of the group CHn results from the
slow reaction from CH3 to C2H4, cf. Fig. 3. The
group of C2H4 and C2H3 molecules has quite a low abundance,
resulting from a slow formation via reaction (18) and a rapid
destruction via reaction (21).
)
molecules and the group n3 of C2H2 and C2H have
significant abundances. The high abundance of the group CHn results from the
slow reaction from CH3 to C2H4, cf. Fig. 3. The
group of C2H4 and C2H3 molecules has quite a low abundance,
resulting from a slow formation via reaction (18) and a rapid
destruction via reaction (21).
The rather high abundance of the group n3 results from the slow loss via reaction (28) due to the low abundance of free oxygen atoms O. The dashed lines in Fig. 4 show the concentration of free oxygen atoms and of OH, which are responsible for the oxidation processes (2), (27), and (28). Figure 4 also shows the abundance of free H atoms, which is important for the basic reaction (4) and for the hydrogen abstraction/addition equilibrium.
The dash-dotted line in Fig. 4 shows the rate of carbon
oxidation (2) normalised by its peak value. The steep increase
at ![]() 1 AU with decreasing radius is due to the steep increase of the
concentration of OH with increasing temperature and the rapid decline is due to
the rapid combustion of carbon. The production of hydrocarbons by carbon
combustion is limited to a narrow cylinder within in the disc centred in our
model on
1 AU with decreasing radius is due to the steep increase of the
concentration of OH with increasing temperature and the rapid decline is due to
the rapid combustion of carbon. The production of hydrocarbons by carbon
combustion is limited to a narrow cylinder within in the disc centred in our
model on ![]() 0.5 AU. The products then are distributed across the whole
disc by turbulent mixing.
0.5 AU. The products then are distributed across the whole
disc by turbulent mixing.
The carbon combustion starts at about 950 K, peaks at about 1150 K and comes to completion at about 1300 K. In this temperature regime the methane is formed and part of the solid carbon is converted into CO. At an only slightly higher temperature than that where carbon black oxidation peaks the methane is converted into C2H2. Since free oxygen atoms appear in non negligible abundances only at temperatures where corundum is already vaporised, the oxidation of C2H2 to CO is only possible in the hot region where all dust is vaporised. As a result, in a broad intermediate region a rather high acetylene abundance piles up in the gas phase, though the element mixture of the disc material is carbon rich and no acetylene could exist in this mixture under chemical equilibrium conditions.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2983f5.eps}\end{figure}](/articles/aa/full/2002/28/aah2983/Timg234.gif) |
Figure 5:
Radial variation of the concentration of the combustion products
of carbon. The concentrations are normalised by the concentration of C nuclei.
Model with
|
Figure 5 shows the concentration of the individual molecules
normalised to the concentration of C nuclei. Methane CH4 and acetylene
C2H2 are the dominating combustion products which can be found all over
the disc. All other hydrocarbons included in this calculation have low
abundances. The abundance of CH4 and C2H2 relative to CO is typically
of the order of 0.8% in the region beyond ![]() 10 AU where the
cometesimals are thought to be formed, which filled the Oort cloud and which
are now observed as long period comets.
10 AU where the
cometesimals are thought to be formed, which filled the Oort cloud and which
are now observed as long period comets.
The small hump in the abundance of molecules of group 1 at about 0.2 AU results from the onset of acetylene oxidation, which is accompanied by CH production.
For comparison Fig. 6 shows the concentration of the products of carbon oxidation if radial mixing is neglected, but inwards drift of the disc material is retained in the model calculation. The results are very different from what one obtains with radial mixing. First, one finds no hydrocarbons in the outer disc regions, as is to be expected. Second, the abundances of CH4 and of C2H2 in the oxidation region are higher than in the case where radial mixing is considered. The results obtained without mixing are essentially the same as that obtained in Finocchi et al. (1997a), except that here no ion-molecule reactions are considered. Comparison of Figs. 5 and 6 clearly shows that radial mixing is of fundamental importance for the chemistry in the protoplanetary disc.
The abundances of the molecules in models with higher or lower accretion rate
are quite similar to the results for the model with
![]() at radii corresponding the same midplane temperature and are not
shown for this reason.
at radii corresponding the same midplane temperature and are not
shown for this reason.
The present calculation refers to a stationary disc model. In time dependent disc models material from the inner disc region is not mixed in significant quantities into the region beyond about 30 AU during the first 106 years of disc evolution (Wehrstedt & Gail 2002; Bockelée-Morvan 2002). The present calculation, thus, only demonstrates that some quantities of the oxidation products of carbon are mixed into the cold disc regions beyond 10 AU where cometary nuclei are thought to be formed, but the results of this model cannot predict quantitatively correct the amounts of hydrocarbons from carbon oxidation in the outer disc. This holds especially for the region beyond about 30 AU into which diffusional transport cannot mix material from the warm inner disc region during the lifetime of the gaseous disc of probably 107. This region requires to study diffusional mixing coupled with time dependent disc models. Such calculations are currently under way.
Figure 5 shows the radial variation of the concentration of CO
and CO2, resulting from the solution of the transport-reaction-diffusion
equation. As it is to be expected, there exist a region in the disc where most
of the gas-phase carbon is not bound in CO but in CO2. The abundance of
CO2 peaks in our model for
![]() at
r=2.2 AU or at a midplane temperature of T=300 K. Equal abundances of CO
and CO2 are encountered at r=2.05 AU or T=400 K and at r=17.5 AU or
T=50 K. Between these radii CO2 is the dominant carbon bearing gas-phase
species, not CO.
at
r=2.2 AU or at a midplane temperature of T=300 K. Equal abundances of CO
and CO2 are encountered at r=2.05 AU or T=400 K and at r=17.5 AU or
T=50 K. Between these radii CO2 is the dominant carbon bearing gas-phase
species, not CO.
The CO2 in the outer parts of the disk is formed via the reaction CO + H2O
![]() CO2 + H2 at
CO2 + H2 at
![]() AU (for the model with
AU (for the model with
![]() ,
cf. Fig. 6) at a temperature of
about 100 K. This temperature is less than the sublimation limit at 150 K of
H2O ice but the vapour pressure of H2O at 100 K is already
non-negligible.
,
cf. Fig. 6) at a temperature of
about 100 K. This temperature is less than the sublimation limit at 150 K of
H2O ice but the vapour pressure of H2O at 100 K is already
non-negligible.
The abundance of ethane resulting from gas phase reactions of the oxidation products of carbon black turns out to be rather low, cf. Fig. 5. The concentration of C2H5 is even lower. The low abundances result from the rather large destruction rate coefficient k-14 and the small rate coefficient k14 for the formation of C2H5. The formation reactions (58) and (59) contribute little to the formation of C2H6.
Figure 5 also shows the radial variation of the concentration of methanol. The concentration of CH3OH also is low which, again, results from a low efficiency of formation and a higher efficiency of destruction by gas phase reactions.
Radio and infrared observations of comets Hale-Bopp and Hyakutake (cf. Bockelée-Morvan et al. 2000; Crovisier & Bockelée-Morvan 1999) and recently of comet Lee (cf. Mumma et al. 2001) have revealed the existence of a number of hydrocarbons and of some nitrogen and sulphur compounds in the cometary nuclei ice. The abundances of the most abundant of the carbon compounds relative to H2O (abundance = 100) is shown in Table 4 together with results of the present model calculation for a distance of 20 AU from the protosun. With respect to H2O it is assumed that in the outer disc all oxygen not bound in dust, CO, and CO2 is bound in H2O. The numbers for the model calculation refer to the abundances in the gas phase prior to precipitation on grain surfaces. The relative abundance in the ices are somewhat different from the relative abundances in the gas phase, depending on the vapour pressure and the properties of the substances and how easy or difficult it is to incorporate them into the ices. The comparison of the total abundances of the hydrocarbons obtained from the model calculation to their abundances in comets at best can reveal general trends. For a more realistic comparison modeling of the trapping of gases in the ice coatings of dust grains and their incorporation into planetesimals would be required, which is out of the scope of this paper.
| Molecules | Hyakutake | Hale-Bopp | Lee | model |
| H2O | 100 | 100 | 100 | 100 |
| CO | 6-30 | 23 | 1.8 | 21 |
| CO2 | 6 | 18 | ||
| CH4 | 0.7 | 0.6 | 0.81 | 0.21 |
| C2H2 | 0.1 | 0.27 | 0.081 | |
| C2H6 | 0.4 | 0.3 | 0.67 |
|
| CH3OH | 2 | 2.4 | 2.1 |
|
| H2CO | 0.2-1 | 1.1 |
With these caveats in mind an inspection of Table 4 and Fig. 5 shows that the prediction of the model calculation of high abundances of CH4, C2H2 and of CO2 in the region of cometary nuclei formation are in accord with the observed high abundance of these species in comets of the Solar System. The methane and acetylene should exist in considerable amounts in cometary ices for the simple reason that they are formed during the combustion of interstellar carbon dust in warm regions of the protoplanetary disc and are mixed outwards by turbulence induced diffusive transport. Also CO2 is abundant due to its formation from CO in the Jupiter-Saturn region of our Solar System and by diffusive mixing into cooler regions.
The mixing of combustion products from the inner disc region to the cold outer disc region easily explains a high CH4 abundance in the region of comet formation, which otherwise has always been a problem (cf. the discussions in Fegley & Prinn 1989 and in Mumma et al. 1993).
An inspection of Table 4 and Fig. 5 also shows, however, that carbon combustion and radial mixing alone cannot explain all the abundant carbon compounds in cometary ices. The low abundance of ethane C2H6 formed during carbon dust combustion obviously is at odds with its high abundance in comets. The observed ethane either results from a different source or it is formed by chemical processes not included in the present model calculation.
Mumma (1996) and Mumma et al. (1996) proposed an origin of the C2H6 detected in comet Hyakutake from H addition reactions on grain surfaces to C2H2 ice of interstellar origin. Generally a pure gas phase chemistry cannot explain an abundance ratio of C2H6 and CH4 of the order of about unity, even not by ion molecule reactions in molecular clouds. It can be formed however, by hydrogen addition reactions on ice surfaces (e.g. Hasegawa & Herbst 1993; Hiraoka et al. 1998). The same type of reasoning as applied by Mumma et al. (1996) and recently by Mumma et al. (2001) to C2H2 ice of interstellar origin can also be applied to the C2H2 ice resulting from mixing carbon combustion products from the inner disc to outer disc regions. Temperatures are low in the comet nuclei formation region, especially at the disc surface, and free H atoms should be present at least at the disc surface due to irradiation with UV photons and X-rays from the young star (cf. Aikawa & Herbst 1999,1999). The hydrogen addition to C2H2 ice in the protoplanetary disc, then, should at least be responsible for some fraction of the ethane observed in comets or even for most of the methane.
The model calculation also yields a very low abundance of CH3OH, contrary to what is observed in comets. We have not considered H2CO in the present model calculation, but Table 4 of Finocchi et al. (1997a) shows that destruction processes of H2CO are more rapid than production mechanisms, resulting in a low abundance of this molecule if formed by gas-phase reactions. Mumma et al. (2001) argue that the abundant molecules CH3OH and H2CO are the results of H addition to CO on ice surfaces at very low temperature. The cometary abundances of these species then are not related to carbon combustion and radial mixing but to a different production mechanism. In this sense our finding of a low abundance of methanol in the products of carbon combustion in a protoplanetary disc is not in odds with the present finding that a high CH4 and C2H2 in comets may result from carbon combustion and mixing.
Copyright ESO 2002