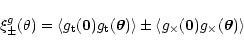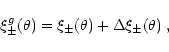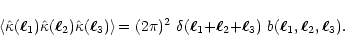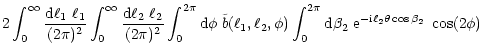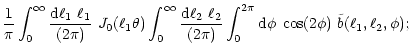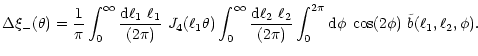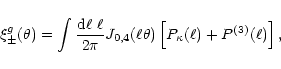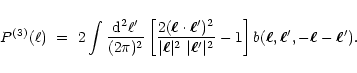Up: B-modes in cosmic shear
The shear is not directly an observable, but is estimated from the
image ellipticities of distant galaxies. The expectation value of the
image ellipticity, however, is not the shear, but the reduced shear
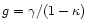 .
Hence, the correlation of the observed
ellipticities is the correlation of the reduced shear, not the shear
itself. In cosmic shear,
.
Hence, the correlation of the observed
ellipticities is the correlation of the reduced shear, not the shear
itself. In cosmic shear,
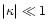 nearly everywhere, and so
the difference between shear and reduced shear shall not play a big
role. However, at least a priori, this effect cannot be neglected, as
seen from the following argument:
nearly everywhere, and so
the difference between shear and reduced shear shall not play a big
role. However, at least a priori, this effect cannot be neglected, as
seen from the following argument:
The skewness
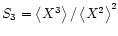 ,
where X is a measure of
shear (such as
,
where X is a measure of
shear (such as
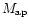 ,
or the reconstructed
,
or the reconstructed 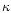 )
has been
calculated by van Waerbeke et al. (2001) to be of order a few hundred.
On a scale of about one arcminute,
)
has been
calculated by van Waerbeke et al. (2001) to be of order a few hundred.
On a scale of about one arcminute,
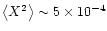 ,
so
that
,
so
that
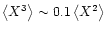 ,
taking
,
taking
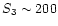 for the
top-hat smoothed
for the
top-hat smoothed 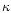 .
The difference between the correlation
functions involving g and those involving
.
The difference between the correlation
functions involving g and those involving 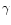 is in principle
of the same order-of-magnitude as
is in principle
of the same order-of-magnitude as
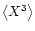 and thus can be present
at the level of a few percent, and there is no reason why it should
not contain a B-mode contribution.
and thus can be present
at the level of a few percent, and there is no reason why it should
not contain a B-mode contribution.
We define the correlation functions
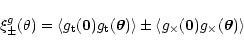 |
(A.1) |
and choose
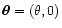 ,
so that
,
so that
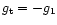 ,
,
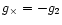 .
Using the approximation
.
Using the approximation
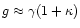 ,
valid for
,
valid for
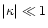 ,
we obtain
,
we obtain
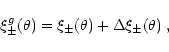 |
(A.2) |
where
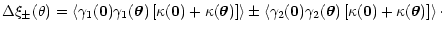 |
|
|
(A.3) |
Replacing the shear and convergence by their Fourier transforms, this
becomes
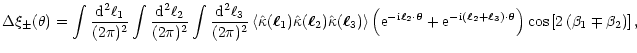 |
|
|
(A.4) |
where, as before, 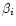 is the polar angle of
is the polar angle of
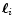 .
The
triple correlator vanishes unless the sum of the wave-vectors equals
zero; one defines the bispectrum by
.
The
triple correlator vanishes unless the sum of the wave-vectors equals
zero; one defines the bispectrum by
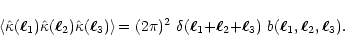 |
(A.5) |
Performing the 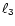 -integration in (A.4) yields
-integration in (A.4) yields
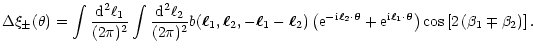 |
|
|
(A.6) |
The function
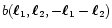 has three
independent arguments, namely the moduli
has three
independent arguments, namely the moduli 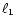 and
and 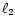 ,
and
the angle
,
and
the angle
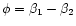 between the two
between the two 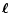 -vectors. We
therefore write
-vectors. We
therefore write
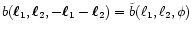 ,
make use of the symmetry in the
integrand of (A.6), and replace the
,
make use of the symmetry in the
integrand of (A.6), and replace the 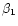 -integration by
one over
-integration by
one over 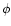 :
:
analogously, one obtains
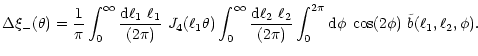 |
|
|
(A.8) |
Inserting these expressions into (19) and making use of (18), one immediately sees that the reduced shear does not
yield any B-mode contribution, and that the correlation functions for
the reduced shear are
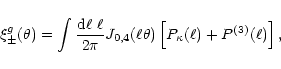 |
(A.9) |
where
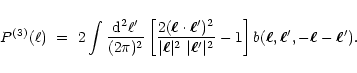 |
(A.10) |
Thus, considering the reduced shear yields an additional E-mode power
to the one obtained from considering the shear itself.


Up: B-modes in cosmic shear
Copyright ESO 2002
![]() .
Hence, the correlation of the observed
ellipticities is the correlation of the reduced shear, not the shear
itself. In cosmic shear,
.
Hence, the correlation of the observed
ellipticities is the correlation of the reduced shear, not the shear
itself. In cosmic shear,
![]() nearly everywhere, and so
the difference between shear and reduced shear shall not play a big
role. However, at least a priori, this effect cannot be neglected, as
seen from the following argument:
nearly everywhere, and so
the difference between shear and reduced shear shall not play a big
role. However, at least a priori, this effect cannot be neglected, as
seen from the following argument:
![]() ,
where X is a measure of
shear (such as
,
where X is a measure of
shear (such as
![]() ,
or the reconstructed
,
or the reconstructed ![]() )
has been
calculated by van Waerbeke et al. (2001) to be of order a few hundred.
On a scale of about one arcminute,
)
has been
calculated by van Waerbeke et al. (2001) to be of order a few hundred.
On a scale of about one arcminute,
![]() ,
so
that
,
so
that
![]() ,
taking
,
taking
![]() for the
top-hat smoothed
for the
top-hat smoothed ![]() .
The difference between the correlation
functions involving g and those involving
.
The difference between the correlation
functions involving g and those involving ![]() is in principle
of the same order-of-magnitude as
is in principle
of the same order-of-magnitude as
![]() and thus can be present
at the level of a few percent, and there is no reason why it should
not contain a B-mode contribution.
and thus can be present
at the level of a few percent, and there is no reason why it should
not contain a B-mode contribution.