We have analyzed the AR faculae and network contrast dependence on both ![]() and the measured magnetic signal, B. It is important to recall that the
observed magnetic signal drops to zero at the limb, even if strong magnetic
field regions are present. This is a straightforward consequence of the fact
that magnetograms are only sensitive to the line-of-sight component of the
magnetic field and that the magnetic field is mainly vertical. To compensate
this effect to first order we have worked with B/
and the measured magnetic signal, B. It is important to recall that the
observed magnetic signal drops to zero at the limb, even if strong magnetic
field regions are present. This is a straightforward consequence of the fact
that magnetograms are only sensitive to the line-of-sight component of the
magnetic field and that the magnetic field is mainly vertical. To compensate
this effect to first order we have worked with B/![]() (i.e.
(i.e.
![]()
![]() )
instead of B. Second order effects due to
radiative-transfer effects or finite thickness of flux tubes remain.
)
instead of B. Second order effects due to
radiative-transfer effects or finite thickness of flux tubes remain.
![\begin{figure}
\par\includegraphics[width=10cm,clip]{H3382f4.ps}\end{figure}](/articles/aa/full/2002/24/aah3382/Timg41.gif) |
Figure 4:
Dependence of the contrast on the absolute value of the magnetogram
signal, corrected for foreshortening effects. The solar disk has been divided
into eight bins, from center to limb. Note that some |
We have binned the B/![]() values into eight intervals that range from the
threshold level of, on average, 15 G to about 600 G. The
intervals have been chosen so that they roughly contain the same number of
pixels each, with the exception of the highest B/
values into eight intervals that range from the
threshold level of, on average, 15 G to about 600 G. The
intervals have been chosen so that they roughly contain the same number of
pixels each, with the exception of the highest B/![]() bins which have fewer
pixels. By sorting the magnetic field strength into different bins we can
distinguish between the CLV of the magnetic features present in regions with
different filling factor
bins which have fewer
pixels. By sorting the magnetic field strength into different bins we can
distinguish between the CLV of the magnetic features present in regions with
different filling factor ![]() .
Figure 3 displays the contrast,
.
Figure 3 displays the contrast,
![]() ,
as a function of
,
as a function of ![]() ,
individually for every B/
,
individually for every B/![]() interval. A second order polynomial has been fitted (employing least squares)
to guide the eye and a dashed line indicating
interval. A second order polynomial has been fitted (employing least squares)
to guide the eye and a dashed line indicating
![]() has been
included for clarity. To avoid overcrowding we have binned data points in sets
of 40 before plotting.
has been
included for clarity. To avoid overcrowding we have binned data points in sets
of 40 before plotting.
Figure 3 reveals a clear evolution of the behaviour of the contrast from
one B/![]() interval to another. Network features (top left panel) show a low
and almost constant contrast, as compared with the very pronounced CLV of the
contrast for active region faculae (bottom panels). Intermediate cases show a
progressive increase of the contrast towards the limb as well as an
increasingly pronounced CLV. When
interval to another. Network features (top left panel) show a low
and almost constant contrast, as compared with the very pronounced CLV of the
contrast for active region faculae (bottom panels). Intermediate cases show a
progressive increase of the contrast towards the limb as well as an
increasingly pronounced CLV. When
![]() G, the contrast peaks at
G, the contrast peaks at
![]() ,
while for magnetic signals B/
,
while for magnetic signals B/
![]() G this maximum
shifts to lower values of
G this maximum
shifts to lower values of ![]() (see Fig. 8 and its discussion in the
text for a more quantitative analysis). Note also that for B/
(see Fig. 8 and its discussion in the
text for a more quantitative analysis). Note also that for B/
![]() G the contrast is negative around disk center, while it is positive in
the network (i.e. for smaller
G the contrast is negative around disk center, while it is positive in
the network (i.e. for smaller ![]() ). We will return to this point in
Sect. 4. The large fluctuations of the contrast near the limb for
intermediate and high magnetic signals are due to the distribution of active
regions on the ten selected days.
). We will return to this point in
Sect. 4. The large fluctuations of the contrast near the limb for
intermediate and high magnetic signals are due to the distribution of active
regions on the ten selected days.
Figure 4 shows the contrast as a function of B/![]() ,
for different
positions on the solar disk. The solar disk has been divided into eight bins of
,
for different
positions on the solar disk. The solar disk has been divided into eight bins of
![]() ,
centred on
,
centred on ![]() values ranging from 0.96 (disk center, top left) to 0.3
(limb, bottom right). Note that to keep the number of points in each bin
approximately equal,
values ranging from 0.96 (disk center, top left) to 0.3
(limb, bottom right). Note that to keep the number of points in each bin
approximately equal, ![]() -bins lying closer to the limb are wider than the
ones around
-bins lying closer to the limb are wider than the
ones around ![]() ,
showing therefore some overlap. Each point of the figure
is obtained by binning together 40 points of data with similar B/
,
showing therefore some overlap. Each point of the figure
is obtained by binning together 40 points of data with similar B/![]() ,
and
second degree polynomials have also been plotted, as in Fig. 3.
,
and
second degree polynomials have also been plotted, as in Fig. 3.
This figure shows that, in general, the contrast initially increases with
B/![]() before decreasing again. We expect it to continue decreasing for even
larger values of B/
before decreasing again. We expect it to continue decreasing for even
larger values of B/![]() representing pores and sunspots. At large
representing pores and sunspots. At large ![]() the
initial increase is small and the contrast basically decreases with B/
the
initial increase is small and the contrast basically decreases with B/![]() ,
while at small
,
while at small ![]() it mainly increases. For
it mainly increases. For ![]() ,
points with large
B/
,
points with large
B/![]() show a negative contrast (as in the lower panels of Fig. 3),
while points at the limb always have positive contrasts. The bins with
show a negative contrast (as in the lower panels of Fig. 3),
while points at the limb always have positive contrasts. The bins with
![]() do not display data for high magnetic signals, because their
intensity is below the intensity threshold.
do not display data for high magnetic signals, because their
intensity is below the intensity threshold.
Given the regular behaviour of the contrast as a function of ![]() and
magnetogram signal,
and
magnetogram signal,
![]() ,
it seems appropiate to
search for an analytical expression for this dependence. We have performed a
multivariate analysis using a
,
it seems appropiate to
search for an analytical expression for this dependence. We have performed a
multivariate analysis using a
![]() grid. The
grid. The ![]() values have been
binned linearly, with
values have been
binned linearly, with
![]() .
B/
.
B/![]() bins have been chosen to be
equally spaced on a logarithmic scale, with
bins have been chosen to be
equally spaced on a logarithmic scale, with
![]() ,
in order
to compensate for the fact that magnetic signals are mostly concentrated
towards lower values (Figs. 3 and 4). The dimensions of the
grid are
,
in order
to compensate for the fact that magnetic signals are mostly concentrated
towards lower values (Figs. 3 and 4). The dimensions of the
grid are
![]() and
and
![]() ,
resulting in a
,
resulting in a ![]() bins grid. We do not consider points with B/
bins grid. We do not consider points with B/![]() G to exclude
bright features that might belong to pores observed near the limb. We are aware
of the fact that 600 G is an arbitrary value for such a cutoff.
G to exclude
bright features that might belong to pores observed near the limb. We are aware
of the fact that 600 G is an arbitrary value for such a cutoff.
Each bin of the grid is defined by the averaged values of the contrast, ![]() and B/
and B/![]() ,
over all the data points of that bin. Although the curves in
Fig. 3 are only intended to guide the eye, they do reveal that second
order polynomials fit the contrast as a function of
,
over all the data points of that bin. Although the curves in
Fig. 3 are only intended to guide the eye, they do reveal that second
order polynomials fit the contrast as a function of ![]() well. We have fitted
the bidimensional array of contrasts by a second order polynomial function of
well. We have fitted
the bidimensional array of contrasts by a second order polynomial function of
![]() and a cubic function of B/
and a cubic function of B/![]() of the form:
of the form:
The terms of Eq. (2) are grouped in Eq. (3) to make clearer the
quadratic dependence of
![]() on
on ![]() and the cubic
dependence on
and the cubic
dependence on ![]() .
When B/
.
When B/![]() is small (< 100 G), the first order
term in B/
is small (< 100 G), the first order
term in B/![]() provides the dominant contribution. When B/
provides the dominant contribution. When B/![]() is large
(
is large
(
![]() G), first and second order terms in B/
G), first and second order terms in B/![]() dominate the
contrast, modulated by the contribution of the cubic term which plays a role in
this range of magnetic signals. At disk center (
dominate the
contrast, modulated by the contribution of the cubic term which plays a role in
this range of magnetic signals. At disk center (![]() ,
those terms result in
a dominant negative contribution (Fig. 3). Note that the contrast is
constrained to go through zero when B/
,
those terms result in
a dominant negative contribution (Fig. 3). Note that the contrast is
constrained to go through zero when B/![]() ,
as expected for the quiet Sun.
,
as expected for the quiet Sun.
The best-fit surface is shown in Fig. 5. The grid corresponds to the
linear ![]() -bins and the logarithmic B/
-bins and the logarithmic B/![]() -bins taken for the fit. The
shape of this surface is quite congruent with that shown by the observed
contrast in Figs. 3 and 4. Note that the function given in
Eq. (3) is valid only for the wavelength and spatial resolution of the
MDI data, 6768 Å and
-bins taken for the fit. The
shape of this surface is quite congruent with that shown by the observed
contrast in Figs. 3 and 4. Note that the function given in
Eq. (3) is valid only for the wavelength and spatial resolution of the
MDI data, 6768 Å and ![]() , respectively. For other values of
these parameters we expect another dependence on
, respectively. For other values of
these parameters we expect another dependence on ![]() and B/
and B/![]() .
In
particular, the absolute value of the contrast is expected to change.
.
In
particular, the absolute value of the contrast is expected to change.
To better estimate how this analytical surface fits the behaviour of the
measured contrasts, we have sliced the surface in both directions, ![]() and
magnetograph signal, and then compared the result with the measured values. In
Fig. 6 the fitted surface is sliced along the
and
magnetograph signal, and then compared the result with the measured values. In
Fig. 6 the fitted surface is sliced along the ![]() -axis (solid
curve), at three sample magnetic signal ranges, representative of low (top
panel), medium (middle panel) and high (lower panel) B/
-axis (solid
curve), at three sample magnetic signal ranges, representative of low (top
panel), medium (middle panel) and high (lower panel) B/![]() values. Dots
represent measured contrasts. To avoid very crowded plots each dot represents
250 (top panel), 100 (middle) and 25 (bottom) data points, respectively. The
different amounts of binning reflect the non-uniform distribution of points
over the B/
values. Dots
represent measured contrasts. To avoid very crowded plots each dot represents
250 (top panel), 100 (middle) and 25 (bottom) data points, respectively. The
different amounts of binning reflect the non-uniform distribution of points
over the B/![]() range. The multivariate regression surface fits quite well
the plotted dependence of the contrast, although minor deviations are visible
at small B/
range. The multivariate regression surface fits quite well
the plotted dependence of the contrast, although minor deviations are visible
at small B/![]() .
Figure 7 shows slices of the modeled surface along
the B/
.
Figure 7 shows slices of the modeled surface along
the B/![]() axis (solid curves) and the corresponding binned data (dots), at
three sample positions on the solar disk, from disk center (top panel) to near
the limb (lower panel). The fitted curves now deviate somewhat more from the
data points, most significantly for
axis (solid curves) and the corresponding binned data (dots), at
three sample positions on the solar disk, from disk center (top panel) to near
the limb (lower panel). The fitted curves now deviate somewhat more from the
data points, most significantly for
![]() ,
where the
discrepancy can reach 0.01 in contrast.
,
where the
discrepancy can reach 0.01 in contrast.
![\begin{figure}
\includegraphics[width=6.8cm,clip]{H3382f7.ps}\end{figure}](/articles/aa/full/2002/24/aah3382/Timg65.gif) |
Figure 7:
The same as Fig. 6, but for cuts along the B/ |
The multivariate analysis yields to an expression for the contrast of
photospheric bright features,
![]() ,
that cannot be
directly compared with previous studies because, to our knowledge, no similar
work has been done before. Quadratic functions have already been used by other
authors (e.g. Foukal 1981) to fit the dependence of the facular contrast
on position over the disk, although most of them use a function of the form
,
that cannot be
directly compared with previous studies because, to our knowledge, no similar
work has been done before. Quadratic functions have already been used by other
authors (e.g. Foukal 1981) to fit the dependence of the facular contrast
on position over the disk, although most of them use a function of the form
![]() (Chapman 1980). A quadratic
function agrees quite well with the CLV proposed by the hot wall model. A cubic
function has been used for fitting the dependence of the contrast on magnetic
strength. In this case we do not have a physical reason, only the goodness of
the fit with respect to other bivariate functional dependences tried (see
Figs. 6 and 7) and the requirement to force the contrast
through zero for a disappearing magnetic signal. We suspect that, in order to
obtain a better empirical description of the dependence of facular contrast on
(Chapman 1980). A quadratic
function agrees quite well with the CLV proposed by the hot wall model. A cubic
function has been used for fitting the dependence of the contrast on magnetic
strength. In this case we do not have a physical reason, only the goodness of
the fit with respect to other bivariate functional dependences tried (see
Figs. 6 and 7) and the requirement to force the contrast
through zero for a disappearing magnetic signal. We suspect that, in order to
obtain a better empirical description of the dependence of facular contrast on
![]() and B/
and B/![]() ,
a larger number of free parameters is required.
,
a larger number of free parameters is required.
The dependence of the peak of
![]() on
on ![]() is shown in
Fig. 8. The
is shown in
Fig. 8. The ![]() -values at which
-values at which
![]() peaks,
peaks,
![]() ,
have been represented against the corresponding magnetic
signal in Fig. 8a. Figure 8b shows the peak
,
have been represented against the corresponding magnetic
signal in Fig. 8a. Figure 8b shows the peak
![]() values reached,
values reached,
![]() (see Fig. 3),
plotted as a function of
(see Fig. 3),
plotted as a function of ![]() .
Finally Fig. 8c shows
.
Finally Fig. 8c shows
![]() plotted against
plotted against ![]() or, in other
words, the dependence on the magnetic signal of the specific contrast per unit
of magnetic flux. Errors in
or, in other
words, the dependence on the magnetic signal of the specific contrast per unit
of magnetic flux. Errors in ![]() are estimated from the difference between the
peak of the best-fit curves in Fig. 3 and the peak obtained directly
from the data points. Error bars in
are estimated from the difference between the
peak of the best-fit curves in Fig. 3 and the peak obtained directly
from the data points. Error bars in ![]() correspond to the size of the
correspond to the size of the
![]() -intervals used in Fig. 3.
-intervals used in Fig. 3.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{H3382F8.ps}\end{figure}](/articles/aa/full/2002/24/aah3382/Timg67.gif) |
Figure 8:
Dependence on the magnetic flux per pixel, |
A linear regression adequately describes the dependence of
![]() on
on ![]() for the precision achievable with the current data. The best fit
straight line (solid line in Fig. 8a) is
for the precision achievable with the current data. The best fit
straight line (solid line in Fig. 8a) is
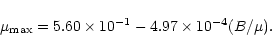 |
(4) |
Copyright ESO 2002