The Solar Oscillations Investigation/Michelson Doppler Imager (SOI/MDI)
instrument is a state-of-the-art helioseismology experiment and magnetograph on
board the SOHO spacecraft, devoted to study the interior structure and dynamics
as well as the surface magnetic field of the Sun. This instrument gives an
image of the Sun on a
![]() CCD camera, and can observe in two
spatial resolution modes, full disk and high-resolution of the central part of
the disk (HR). We are interested in the full disk measurements, which have a
field of view of
CCD camera, and can observe in two
spatial resolution modes, full disk and high-resolution of the central part of
the disk (HR). We are interested in the full disk measurements, which have a
field of view of
![]() and a pixel size of
and a pixel size of
![]() .
Two tunable Michelson interferometers allow MDI to
record filtergrams centered at five wavelengths across the Ni I 6768
Å absorption line. From the filtergrams, MDI computes the following
six observables: Doppler velocity, continuum intensity, line depth,
longitudinal magnetic field, horizontal velocity and limb position. The SOI/MDI
instrument is described in detail by Scherrer et al. (1995).
.
Two tunable Michelson interferometers allow MDI to
record filtergrams centered at five wavelengths across the Ni I 6768
Å absorption line. From the filtergrams, MDI computes the following
six observables: Doppler velocity, continuum intensity, line depth,
longitudinal magnetic field, horizontal velocity and limb position. The SOI/MDI
instrument is described in detail by Scherrer et al. (1995).
The products of interest for our work are the full disk magnetograms and
continuum intensity images. Magnetograms only measure net magnetic flux per
resolution element, therefore the signal is not the true magnetic field
strength B, inside a flux tube, but its longitudinal component,
![]() ,
averaged over the pixel, where
,
averaged over the pixel, where ![]() is the
angle between the magnetic vector and the line of sight. For simplicity, we
hereafter refer to
is the
angle between the magnetic vector and the line of sight. For simplicity, we
hereafter refer to
![]() as B. In a 2-component
model of the magnetic field, with magnetic flux tubes of field strength B
covering a fraction
as B. In a 2-component
model of the magnetic field, with magnetic flux tubes of field strength B
covering a fraction ![]() of the solar surface separated by a field-free
component covering
of the solar surface separated by a field-free
component covering
![]() of the surface, we can write
of the surface, we can write
![]() as
as
![]() .
Since the true field
strength
.
Since the true field
strength ![]() lies in a relatively narrow range of 1000-1500 G for
all magnetic features except intranetwork elements (Solanki et al.
1999), and
lies in a relatively narrow range of 1000-1500 G for
all magnetic features except intranetwork elements (Solanki et al.
1999), and
![]() is a reasonable
approximation (
is a reasonable
approximation (![]() is the heliocentric angle), the strength of the
magnetogram signal mainly provides information on the magnetic filling factor
is the heliocentric angle), the strength of the
magnetogram signal mainly provides information on the magnetic filling factor
![]() .
.
MDI magnetograms are usually obtained every 96 min, with the exception of
periodic campaigns in which 1-min cadence measurements are available. The
1-![]() noise level for a one-min longitudinal magnetogram is 20
G. Full disk continuum intensity images are taken each minute with a
noise level of 0.3%.
noise level for a one-min longitudinal magnetogram is 20
G. Full disk continuum intensity images are taken each minute with a
noise level of 0.3%.
The analyzed data set consists of nearly simultaneous magnetograms and
continuum intensity images recorded on 10 days in the period February to
October, 1999, as shown in Table 1. The time of the observations is
given for the averaged magnetograms (see Sect. 2.2). It corresponds
to the middle of the 20 min integration time. These days were chosen because
they belong to a high activity period so that everything from quiet network to
intense active-region plage was present on the solar surface. The sample
contains active regions spread over almost all
![]() values. They
are also generally well separated in time in order to avoid duplication.
values. They
are also generally well separated in time in order to avoid duplication.
| 1999 observation dates | Time (UT) |
| February 13 | 00:10:02 |
| February 20 | 04:10:02 |
| May 14 | 00:10:03 |
| May 28 | 06:10:03 |
| June 25 | 01:10:02 |
| July 2 | 03:10:02 |
| July 10 | 01:10:02 |
| August 7 | 00:10:02 |
| October 12 | 09:10:03 |
| October 15 | 06:10:03 |
We employ averages over 20 single magnetograms, taken at a cadence of 1 per
minute, in order to reduce the noise level sufficiently to reliably identify
the quiet network. The individual magnetograms were rotated to compensate for
the time difference before averaging. Intensities are standard 1-min images.
Care has been taken to use intensity images obtained as close in time to the
magnetograms as possible. In all cases but one, the two types of images were
recorded within 30 min of each other, with 37 min being the highest
difference. The intensity images have been rotated to co-align them with the
corresponding average magnetogram. Intensity images have also been corrected
for limb-darkening effects using a fifth order polynomial in ![]() following
Neckel & Labs (1994). Our final data sets are pairs of co-aligned
averaged magnetograms and photospheric continuum intensity images for each of
the 10 selected days. Both types of images can be compared pixel by pixel. An
example magnetogram and the corresponding intensity image recorded on October
12, 1999 are shown in Fig. 1 (top and middle panels).
following
Neckel & Labs (1994). Our final data sets are pairs of co-aligned
averaged magnetograms and photospheric continuum intensity images for each of
the 10 selected days. Both types of images can be compared pixel by pixel. An
example magnetogram and the corresponding intensity image recorded on October
12, 1999 are shown in Fig. 1 (top and middle panels).
We have determined the noise level of the MDI magnetograms and continuum images
as a function of position over the CCD array. The standard deviation for the
magnetic signal has been calculated using a running
![]() pixel box
over the solar disk, with the exception of the limbs, which were avoided by
masking out an outer ring of 75 pixels width. This process was applied to
several 1996 low activity magnetograms, in order to avoid artifacts introduced
by the presence of active regions. After that, their median was determined to
eliminate the possible remaining activity. A second order surface was then
fitted to the result and extrapolated to cover the whole solar disk. The
resulting noise level,
pixel box
over the solar disk, with the exception of the limbs, which were avoided by
masking out an outer ring of 75 pixels width. This process was applied to
several 1996 low activity magnetograms, in order to avoid artifacts introduced
by the presence of active regions. After that, their median was determined to
eliminate the possible remaining activity. A second order surface was then
fitted to the result and extrapolated to cover the whole solar disk. The
resulting noise level,
![]() ,
shows an increase towards the
SW limb that probably includes some velocity signal leakage. In Fig. 2
we show the calculated standard deviation for the 20-min averaged
magnetograms. Note that when applying this noise surface to our data we have
assumed that the MDI noise level has remained unchanged between 1996 and 1999.
,
shows an increase towards the
SW limb that probably includes some velocity signal leakage. In Fig. 2
we show the calculated standard deviation for the 20-min averaged
magnetograms. Note that when applying this noise surface to our data we have
assumed that the MDI noise level has remained unchanged between 1996 and 1999.
A similar procedure has been used to determine the mean and standard deviation
of the quiet Sun continuum intensity for each selected day,
![]() and
and
![]() respectively, where the
subscript
respectively, where the
subscript ![]() denotes "quiet Sun". Every pixel in the running mean
box with an absolute magnetic signal value below 0.5 times
denotes "quiet Sun". Every pixel in the running mean
box with an absolute magnetic signal value below 0.5 times
![]() (i.e. pixels with corresponding magnetogram signal
between approximately -2.5 and 2.5 G) has been considered as a quiet
Sun pixel.
(i.e. pixels with corresponding magnetogram signal
between approximately -2.5 and 2.5 G) has been considered as a quiet
Sun pixel.
The surface distribution of solar magnetic features that produce a bright
contribution to irradiance variations, is identified by setting two thresholds
to every magnetogram-intensity image pair. The first threshold looks for
magnetic activity of any kind, and is set to
![]() ,
which
corresponds, on average, to 15 G. As we are only interested in bright
magnetic features, the second threshold masks out sunspots and pores by setting
all pixels with a continuum intensity
,
which
corresponds, on average, to 15 G. As we are only interested in bright
magnetic features, the second threshold masks out sunspots and pores by setting
all pixels with a continuum intensity
![]() below the
average to a null value. To reduce false detections, even at the risk of
missing active pixels, we reject all isolated pixels above the given thresholds
assuming that they are noise.
below the
average to a null value. To reduce false detections, even at the risk of
missing active pixels, we reject all isolated pixels above the given thresholds
assuming that they are noise.
![]() out of 107 analyzed data points are
rejected in this way. After this step, we find that 6% of the pixels satisfy
both criteria. Using both thresholds we construct a mask of the contrast of
bright features for each day. The result of applying the mask derived from the
magnetogram (top panel) and intensity image (middle panel) shown in
Fig. 1, is displayed in the bottom panel of that figure. Note that
only features that lie above the given thresholds in the magnetogram and the
intensity image are indicated by white pixels. Sunspots near the NE limb, for
example, do not appear in the mask, but faculae surrounding those sunspots are
well identified. Smaller features belonging to the magnetic network are also
pinpointed outside of the active regions, although weaker elements of the
network may well be missed. For each pixel with coordinates (x,y), the
contrast
out of 107 analyzed data points are
rejected in this way. After this step, we find that 6% of the pixels satisfy
both criteria. Using both thresholds we construct a mask of the contrast of
bright features for each day. The result of applying the mask derived from the
magnetogram (top panel) and intensity image (middle panel) shown in
Fig. 1, is displayed in the bottom panel of that figure. Note that
only features that lie above the given thresholds in the magnetogram and the
intensity image are indicated by white pixels. Sunspots near the NE limb, for
example, do not appear in the mask, but faculae surrounding those sunspots are
well identified. Smaller features belonging to the magnetic network are also
pinpointed outside of the active regions, although weaker elements of the
network may well be missed. For each pixel with coordinates (x,y), the
contrast
![]() is defined as:
is defined as:
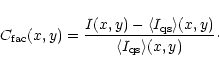 |
(1) |
The method used in this work resembles that employed by Topka et al. (1992, 1997), although our magnetic threshold is much lower due to the less noisy magnetograms used. The angular resolution, however, is also considerably lower, but it is constant.
Copyright ESO 2002