$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{f3_new.eps}}\end{figure}$

Figure 3: Comparison of the $\Omega = 16 \mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ model with kinematic maps. The axes in all panels are sky positions. a) and c) are maps of mean line-of-sight velocity, and velocity dispersion, respectively, taken from the "M 8'' data of Bacon et al. (2001); b) and d) are predictions of our model, including a constant bulge velocity dispersion of $150\mbox{~km~ s${}^{-1}$ }$ , and smoothed with a Gaussian beam of $FWHM= 0 \farcs 5$ . In a) and b), the dotted line is the zero-velocity curve, and successive isocontours are in steps of $25\mbox{~km~ s${}^{-1}$ }$ ; positive (negative) velocities are in light (dark) shades. The dotted line in c) and d) corresponds to velocity dispersion of $200\mbox{~km~ s${}^{-1}$ }$ , successive isocontours are in steps of $25\mbox{~km~ s${}^{-1}$ }$ , and lighter shades indicate higher values.

We restored the Sérsic bulge profile, for comparisons with the photometry - see Figs. 2c and 2d, where the $\Omega = 16 \mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ model is compared with the photometry of Lauer et al. (1998). The locations of the peaks agree, although the model runs out of orbits near the edges. For kinematic comparisons, we further assumed that the velocity distribution of the bulge stars was Gaussian, with $\sigma_v=150\mbox{~km~ s${}^{-1}$ }$ . 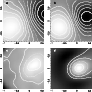Figure 3 compares the model with the kinematic maps of Bacon et al. (2001). The need to smooth with a beam of $FWHM= 0 \farcs 5$ , rendered the absence of the outer orbits more acute. However, the zero velocity curves, as well as the orientation of the line joining the maximum and minimum velocities are in agreement (Figs. 3a and 3b); the dispersion maps are reasonably compatible in the region of the peak near P2 (Figs. 3c and 3d). As noted earlier, the best fits obtained for models with $\Omega = 15,~ 16,~\mbox{and}~ 17\mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ . In Figs. 4a-4c, these are compared with the photometry of Lauer et al. (1998), and HST STIS kinematics from Bacon et al. (2001). Together, they should give some idea of the deviations from observations. The pattern speed has been variously estimated (Sambhus & Sridhar 2000; Salow & Statler 2001; Bacon et al. 2001) to lie between 3 and $25\mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ . Our present estimate, $\Omega\simeq 16\mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ , is closest to Salow & Statler (2001) who, however, prefer to view the disk at the traditional inclination of $77{\degr}$ .

We note here some limitations of our dynamical models. A basic assumption of our procedure was that the nuclear disk is razor-thin, and inclined at an angle of $(77^{\circ}-51.54^{\circ}) \simeq 25^{\circ}$ , with respect to the plane of the larger galactic disk of M 31. We also ignored the gravitational force of the bulge stars on the nuclear disk, because the net effect of a spherically symmetric bulge would be to only modify the precession rates by a small amount. However, it is known (Kent 1983, 1989) that the bulge of M 31 is flattened, and this can be expected to modify the models in at least two ways. If the flattened bulge were treated as a fixed, external potential, the node of the nuclear disk will precess. The more serious effect arises from the dynamical friction of the bulge, acting on the stars composing the nuclear disk. The torque exerted by a flattened bulge, whose stars could have anisotropic distributions of velocities, could well decrease the inclination of the disk. However, we have not been able to estimate the response of the stellar disk, whose structure is so fundamentally determined by eccentric orbits locked in resonance.

The assumption that the nuclear disk is razor-thin is, of course, unrealistic. Tremaine (1995) estimates that two-body relaxation would thicken the disk significantly, within a Hubble time. Our choice of a razor-thin disk was made primarily for the recovery of a "unique'' surface density distribution for the disk in its plane (Fig. 1c), from the observed surface photometry (Fig. 1a). This surface density was then used to calculate the disk self-gravity, possible orbit families for a range of pattern speeds, and then populating the orbit libraries appropriately using the RL algorithm. Consideration of a thick disk would have introduced an infinity of possible choices in the very first step of our procedure, and we wished to avoid it. It should, however, be stressed that an uninclined thick disk could well be compatible with observed photometry. This possibility should certainly be explored, perhaps by including kinematic data as additional constraints. A question that no one, presenting stellar dynamical models, can afford to ignore is whether the system is stable. There appears to be no better route to address this question, than N-body simulations. In this light we should regard the models presented in this paper as plausible guesses for further numerical explorations.

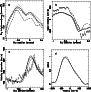$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{f4_new.eps}}\end{figure}$

Figure 4: Further comparisons of models and observations. In a), b), and c), the dashed-dot, solid, and dashed lines correspond to predictions of our model disks (including the bulge), with $\Omega = 15,~ 16,~\mbox{and}~ 17\mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ . The dotted line in a) is a cut along the P1-P2 line of the observed brightness, shown in Fig. 3a. In b) and c), the plotted data points are HST STIS observations (from Bacon et al. 2001), of mean line-of-sight velocity and velocity dispersion, respectively, taken with a slit of width equal to $0 \farcs 1$ , placed at PA of $39{\degr}$ . The three lines represent similar "observations'' of our models. In d) we plot the LOSVD, observed with a Gaussian beam of $FWHM= 0 \farcs 21$ , for the $\Omega = 16 \mbox{~km~ s${}^{-1}$ ~ pc${}^{-1}$ }$ model (including bulge), centered on the MDO. The dashed line was computed after suppressing the retrograde orbits.

The "eccentricity'' profiles of the loop orbits are given in Fig. 5a. The prograde loops have a characteristic non monotonic profile, whereas the retrograde loops have large eccentricites that increase monotonically with size, to the biggest orbits employed in our models. We note that the eccentricity profile of the prograde orbits is quite different from Salow & Statler (2001): in particular, there is no tendency for them to switch apoapses to the anti-P1 side of the MDO. The profiles of the apoapse angles (Fig. 5b) show no evidence for spirality; prograde/retrograde loops have their apoapses on the P1/anti-P1 side of the MDO. The disk mass is $1.4\times 10^7~M_{\odot}$ , with 3.4% on retrograde orbits; the central LOSVD in Fig. 4d indicate the positive and negative velocities at which the latter contribute. We have tried models with only prograde loops, but these gave consistently poor fits around P2.

$\begin{figure} \par\resizebox{8.3cm}{!}{\includegraphics{f5.eps}}\end{figure}$

Figure 5: Distribution of orbital eccentricities and apoapse angles, with orbit size. The "semi-major axis'' is defined as the mean of the maximum and minimum radii (r_> and r_<) of a parent loop; $\mbox{eccentricity}\equiv (r_{>} - r_{<})/(r_{>} + r_{<})$ . In a) and b) the eccentricity and angle to apoapse, of parent loops, are plotted for a selection of prograde (filled circles) and retrograde (open circles) parent loop orbits. Prograde (retrograde) parents have apoapses on the P1 side (anti-P1 side) of the MDO.

Numerical simulations (Jacobs & Sellwood 2001), and analytical study (Tremaine 2001) indicate that nearly Keplerian disks (without counter-rotating streams) are neutrally stable to linear, m=1 perturbations. Hence it might appear unlikely that the lopsidedness could have grown spontaneously from an initially axisymmetric disk. Note, however, that in Bacon et al. (2001) there is reference to work, to be reported in the future by Combes and Emsellem, on an m=1instability. Bacon et al. (2001) also suggest that a lopsided mode could have been excited by the passage of a massive object, such as a giant molecular cloud, or a globular cluster. They also report supportive simulations, where excited modes remained undamped for $7\times 10^7$ years, with almost constant pattern speed; this is certainly a plausible scenario.

Here we consider an alternative origin of the lopsidedness, based on the presence of the retrograde loops in our models, and recent work by Touma (2001) on a linear instability, in a softened-gravity version of Laplace-Lagrange theory of planetary motions. To the extent that softened-gravity mimics the velocity dispersions of stars (Miller 1971; Erickson 1974), this work suggests that even a few percent of mass in counter-rotating orbits could excite a linear m=1overstability. In an axisymmetric nearly Keplerian disk, the apsides of prograde/retrograde orbits have negative/positive precession rates. A resonant response of the retrograde orbits (to a perturbation with positive $\Omega$ ) appears to excite large eccentricities. This compensates for their small mass fraction, allowing them to act so significantly, that the precession of apsides of the prograde loops is locked to that of the retrograde loops. We note that the large eccentricities of our retrograde loops (Fig. 5a), obtained directly from orbit integrations, are suggestive of this possibility. We speculate further that the overstability (as is common in other contexts) is arrested in growth by nonlinearity, and it settles into a nonlinear, neutral mode. The steadily rotating nuclear disk of M 31 might well be in such a phase. Material on retrograde orbits could have been accreted by the infall of debris into the center of M 31. One possibility is suggested by our estimate of the mass in retrograde orbits in our models, $\sim$ $5\times 10^5~M_{\odot}$ . Tremaine et al. (1975) have argued that dynamical friction would cause globular clusters to spiral in toward galactic nuclei, and tidally disrupt. We could be witnessing the lopsided signature of such an event.

3 Comparisons and conclusions