The observed rotation curve can be decomposed into the contributions of the individual galactic mass constituents (van Albada et al. 1985; Kent 1986, 1987; Begeman et al. 1991). As usual, for the luminous components a constant M/L ratio is adopted. Then for each luminous component a mass model can be constructed proportional to the light distribution which is given by the photometry. The gravitational influence of the gas is included and a dark halo is needed to explain the large rotation in the outer parts of galaxies. The decomposition of the observed rotation curve can then be achieved by a least squares fitting procedure where the individual rotational contributions of disc, bulge, gas, and dark halo are determined. Such a fit is, however, far from unique (van Albada et al. 1986); in general a range of M/L ratios for the disc (and bulge) gives an equally good fit to the data. Additional information or assumptions are needed. One such assumption is the maximum disc hypothesis which states that the contribution of the disc to the rotation should be scaled up as high as possible and so assigning the maximum possible M/L ratio to the disc. On the other hand, observations of the stellar velocity dispersions of galactics discs suggest that the maximum contribution of the disc to the rotation is, on average, 63% at the position where the disc has its maximum velocity (Bottema 1993). As discussed in the introduction, there is other evidence that for normal and specifically for the low surface brightness galaxies the maximum disc hypothesis cannot hold. Below we will investigate the possibilities for NGC 3992.
Photometry in the B, R, I, and
![]() band is given by
Tully et al. (1996), of which the I and
band is given by
Tully et al. (1996), of which the I and
![]() data are reproduced
in Fig. 12. Since the
data are reproduced
in Fig. 12. Since the
![]() data do not extent very far out,
the I band data are used for the mass modelling. Note that in the
inner regions the I and
data do not extent very far out,
the I band data are used for the mass modelling. Note that in the
inner regions the I and
![]() photometry are nearly identical
and hence there are no large population and dust gradients in the
inner regions and the I band gives a good representation of the
actual mass distribution.
The total luminosity of NGC 3992 in the I band is identical to
within the errors with the total luminosity derived by Héraudau
& Simien (1996) which gives confidence that the absolute calibration
of the surface brightness is correct.
The photometry has been cut off at a
radius of 250
photometry are nearly identical
and hence there are no large population and dust gradients in the
inner regions and the I band gives a good representation of the
actual mass distribution.
The total luminosity of NGC 3992 in the I band is identical to
within the errors with the total luminosity derived by Héraudau
& Simien (1996) which gives confidence that the absolute calibration
of the surface brightness is correct.
The photometry has been cut off at a
radius of 250![]() but the calculated rotation curve does not
depend on the exact position of the cutoff as long as it is
at or beyond this 250
but the calculated rotation curve does not
depend on the exact position of the cutoff as long as it is
at or beyond this 250![]() .
.
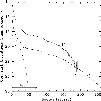 |
Figure 12:
Observed photometric profiles in the I and
|
For the gaseous component a surface distribution equal to that of the H I is taken (see Fig. 6), multiplied with a factor 1.4 to account for helium.
The gas disc is adopted to be infinitely thin.
For the dark halo a pseudo isothermal sphere generally provides
a satisfactory model (Carignan & Freeman 1985) for which the
density distribution ![]() is given by
is given by
![\begin{displaymath}{\rho}_{\rm h} = {\rho}_{\rm h}^0 \left[ 1 + \frac{R^2}{R^2_{\rm core}}
\right]^{-1},
\end{displaymath}](/articles/aa/full/2002/24/aah3038/img86.gif) |
(2) |
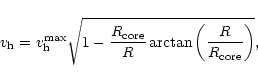 |
(3) |
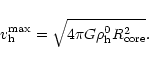 |
(4) |
The decomposition of the observed rotation curve is performed
by fitting the sum of the rotation curves of the components to the
observed data in a least squares sense. In that way the best fit
is designated as the situation of minimum ![]() value.
However, a least squares fit procedure assumes that the fitting
function is known a priori and the data points scatter in a Gaussian
way around that function. For rotation curves that is not valid.
Firstly a rotational functionality for the halo is adopted which need
not be correct. Secondly the procedure to determine the rotation
is an approximation in the sense that azimuthal symmetry is assumed
with no in or outflow. For example spiral arms can produce small
irregularities, which may lead to small systematic deviations from
the actual rotation law. Because of these matters the resulting
minimum
value.
However, a least squares fit procedure assumes that the fitting
function is known a priori and the data points scatter in a Gaussian
way around that function. For rotation curves that is not valid.
Firstly a rotational functionality for the halo is adopted which need
not be correct. Secondly the procedure to determine the rotation
is an approximation in the sense that azimuthal symmetry is assumed
with no in or outflow. For example spiral arms can produce small
irregularities, which may lead to small systematic deviations from
the actual rotation law. Because of these matters the resulting
minimum ![]() value is only a limited indicator of the quality
of the fit. In general one has to make an inspection by eye to judge
the quality of the fit, taking
the errors of the individual data points into account.
value is only a limited indicator of the quality
of the fit. In general one has to make an inspection by eye to judge
the quality of the fit, taking
the errors of the individual data points into account.
First the decomposition results for a disc only situation will be considered.
Three parameters are free and have been fitted simultaneously: the core radius
and maximum rotation of the dark halo, and the M/L ratio of the disc.
The result is illustrated in Fig. 13a
and has a disc with an I-band mass-to-light ratio of
![]() .
Further numerical values
are given now and for the following fits in Table 4.
.
Further numerical values
are given now and for the following fits in Table 4.
| Situation | panel in | red | disc | (M/L) |
bulge | (M/L) |
|
|
| Fig. 13 | mass | mass | ||||||
| (10
|
(
|
(10
|
(
|
(kpc) | (km s-1) | |||
| D only, best fit | a | 1.22 | 73.7 | 1.79 |
- | - | 1.16 |
230 |
| D only, max disc | b | 1.94 | 194.1 | 4.71 |
- | - | 44.9 |
482 |
| D + B, equal M/L | c | 1.22 | 64.9 | 2.03 |
18.7 | 2.03 | 1.79 |
230 |
| D + B,
|
- | 1.25 | 71.3 | 2.23 |
36.9 | 4.0 | 3.7 |
233 |
| D + B, max | d | 1.08 | 134.6 | 4.2 |
47.1 | 5.1 |
23.2 |
327 |
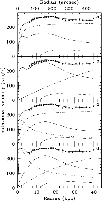 |
Figure 13:
a) to d) Various rotation curve decompositions. The dots
are the observed rotational data. The fit
to these is indicated by the full drawn line.
Individual contributions of the bulge (dotted line), disc (long dashed line),
gas (short dashed line), and dark halo (dash - dot line)
are also given. Details are given in the text and in Table 4.
a)
All the mass is assumed to be in
a disc like distribution. The best fit is for a
disc contributing |
The photometric radial profile clearly indicates that NGC 3992
is highly non exponential, contrary to claims by Elmegreen & Elmegreen
(1985). This galaxy is of an extreme Freeman type II (Freeman 1970)
and the maximum of the rotation does not occur at the usual 2.2
scalelengths, if a scalelength can be defined at all.
Instead the relative exponential part between 50 and 130![]() followed by the more steep decline in brightness beyond, results
in a specific shape of the rotation curve of the luminous
matter as shown by the long dashed line in Fig. 13. This
curve has a maximum around 13 kpc and a long linearly decreasing
section between 17 and 24 kpc.
The observed drop in
the rotation curve is then not a consequence of a truncation feature
of the disc as suggested by G84 but simply a consequence of the
non-exponentiality of the disc. Also the photometry does not suggest
a sudden drop in brightness at a radius of
followed by the more steep decline in brightness beyond, results
in a specific shape of the rotation curve of the luminous
matter as shown by the long dashed line in Fig. 13. This
curve has a maximum around 13 kpc and a long linearly decreasing
section between 17 and 24 kpc.
The observed drop in
the rotation curve is then not a consequence of a truncation feature
of the disc as suggested by G84 but simply a consequence of the
non-exponentiality of the disc. Also the photometry does not suggest
a sudden drop in brightness at a radius of ![]() 19 kpc = 211
19 kpc = 211![]() needed to explain such a drop at the observed radii between
19 and 24 kpc. Some experimenting has been done by taking cut offs in
the photometry at 250
needed to explain such a drop at the observed radii between
19 and 24 kpc. Some experimenting has been done by taking cut offs in
the photometry at 250![]() = 22.5 kpc and at larger radii.
But this is already so far out that an associated drop
in the rotation curve cannot be noticed any more (Casertano 1983).
= 22.5 kpc and at larger radii.
But this is already so far out that an associated drop
in the rotation curve cannot be noticed any more (Casertano 1983).
There is a secondary minimum in the least squares fit, which is
illustrated in Fig. 13b. It is in principle a maximum disc fit
with a dark halo having a core radius comparable to the maximum
radius to where the rotation curve is determined. Compared to the
previous fit, the outer data points seem to be better represented.
In the stellar disc regions however, the fit is worse and at certain
positions not compatible with the data. The reduced minimum ![]() value
for this fit is 1.94, for the previous fit it was 1.22. The mass-to-light
ratio in the I band, uncorrected for absorption amounts to
value
for this fit is 1.94, for the previous fit it was 1.22. The mass-to-light
ratio in the I band, uncorrected for absorption amounts to
![]() for this maximum disc fit.
for this maximum disc fit.
When a bulge is added to the system there is one more free parameter,
namely the M/L ratio of the bulge.
This parameter has been constrained in two ways;
a situation where the M/L ratio is taken equal to that of the disc
(see Fig. 13c)
and a situation where the maximum rotation of the bulge is fixed
at the flat level of the rotation curve.
The fit is performed and dark halo parameters and disc M/L ratios
follow and are given in Table 4.
The reduced ![]() value for both bulge M/L ratios
are equal. What one can achieve by adding a bulge is some mass transfer
from the dark halo to the bulge resulting in a larger core radius
compared to the disc only case. Presently core radii are 1.8 and
3.7 kpc compared to the 1.16 kpc when only a disc is present.
When the M/L ratio of the bulge is not constrained the fitting
procedure generates a result given in Fig. 13d which is analogous
to the maximum disc fit in Fig. 13b. This fit is actually better then
the one where the M/L ratio of the bulge is constrained in the sense
that the reduced
value for both bulge M/L ratios
are equal. What one can achieve by adding a bulge is some mass transfer
from the dark halo to the bulge resulting in a larger core radius
compared to the disc only case. Presently core radii are 1.8 and
3.7 kpc compared to the 1.16 kpc when only a disc is present.
When the M/L ratio of the bulge is not constrained the fitting
procedure generates a result given in Fig. 13d which is analogous
to the maximum disc fit in Fig. 13b. This fit is actually better then
the one where the M/L ratio of the bulge is constrained in the sense
that the reduced ![]() value is slightly lower.
However the M/L ratios are substantial; 5.1 and 4.2
for the bulge and
disc respectively. So adding a bulge has
the side effect that one is again close to the situation for other
rotation curve decompositions: nearly equally good fits can be
made for a whole range of disc contributions to the total rotation.
Other indicators are then
needed to determine the M/L ratio of the disc, like observations of
disc stellar velocity dispersions or population synthesis arguments.
value is slightly lower.
However the M/L ratios are substantial; 5.1 and 4.2
for the bulge and
disc respectively. So adding a bulge has
the side effect that one is again close to the situation for other
rotation curve decompositions: nearly equally good fits can be
made for a whole range of disc contributions to the total rotation.
Other indicators are then
needed to determine the M/L ratio of the disc, like observations of
disc stellar velocity dispersions or population synthesis arguments.
One can conclude that the features in the rotation curve are generated by the strong non-exponentiality of the photometry. Still, even with the determined detailed rotation curve of NGC 3992 it is not possible to get a tight constraint on the disc contribution to the total rotation or on the M/L ratios of disc and bulge. There is only a slight preference for the disc to be sub maximal.
Copyright ESO 2002