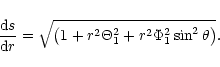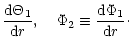Up: Modelling of the surface
In order to model the actual surface magnetic field by
superposition of the star-centered global dipole 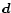 and
the crust-anchored dipole moment
and
the crust-anchored dipole moment 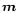 ,
let us consider the
general geometrical situation presented in Fig. 1. The
resultant surface magnetic field is
,
let us consider the
general geometrical situation presented in Fig. 1. The
resultant surface magnetic field is
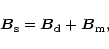 |
(A.1) |
where
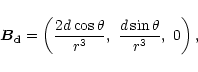 |
(A.2) |
and
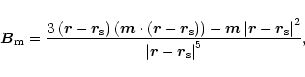 |
(A.3) |
where the spherical components of
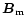 are explicitly given
in Eqs. (A.5). The global magnetic dipole moment
are explicitly given
in Eqs. (A.5). The global magnetic dipole moment
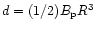 ,
where
,
where
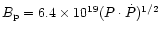 G is the dipole
component at the pole derived from the pulsar spin-down rate, and
the crust-anchored local dipole moment
G is the dipole
component at the pole derived from the pulsar spin-down rate, and
the crust-anchored local dipole moment
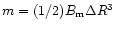 ,
where
,
where
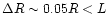 and
and
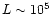 cm is the characteristic crust dimension
(R=106 cm). One can see that a local anomaly can
significantly influence the surface magnetic field
cm is the characteristic crust dimension
(R=106 cm). One can see that a local anomaly can
significantly influence the surface magnetic field
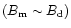 if
if
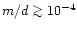 .
We use the star-centered spherical
coordinates with z axis directed along the global magnetic
dipole moment.
Thus,
.
We use the star-centered spherical
coordinates with z axis directed along the global magnetic
dipole moment.
Thus,
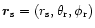 and
and
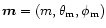 .
.
The equations of the line of force of the vector field
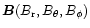 have a well known form in spherical
co-ordinates
have a well known form in spherical
co-ordinates
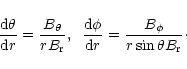 |
(A.4) |
The solution of these equations, with the initial conditions
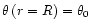 and
and
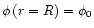 determining a given field line at the surface,
describe the parametric equation of the
field lines. The magnetic field
determining a given field line at the surface,
describe the parametric equation of the
field lines. The magnetic field
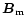 (Eq. (A.3)), as
well as the dipolar magnetic filed
(Eq. (A.3)), as
well as the dipolar magnetic filed
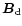 (Eq. (A.2)),
can be written in terms of spherical components
(Eq. (A.2)),
can be written in terms of spherical components
where
According to the geometry presented in Fig. (1), the
components of the radius-vector of the origin of the star-anchored
local dipole moments can be written as
and the components of the local dipole moment are
We now define the boundary of the open field lines by setting
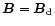 at an altitude
at an altitude
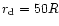 ,
where the magnetic
field should appear like a pure dipole (the numerical results
are quite insensitive to the choice of
,
where the magnetic
field should appear like a pure dipole (the numerical results
are quite insensitive to the choice of 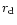 as long as it is few
times R; in fact, already at r=5R the ratio
as long as it is few
times R; in fact, already at r=5R the ratio
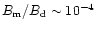 for
for
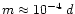 ). Then we solve numerically the system of differential
equations
). Then we solve numerically the system of differential
equations
 |
(A.6) |
 |
(A.7) |
obtained from Eq. (A.4) by substitutions
 ,
,
 and
and
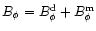 (Eqs. (A.2) and
(A.5)), with the initial conditions
(Eqs. (A.2) and
(A.5)), with the initial conditions
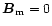 defined at r=50R and trace each field line from altitude
defined at r=50R and trace each field line from altitude
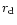 (where
(where
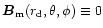 )
down to the stellar surface (<tex2htmlcommentmark>
r=R). Here we defined two functions
)
down to the stellar surface (<tex2htmlcommentmark>
r=R). Here we defined two functions 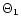 and
and 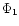 to be
used later in Eqs. (A.10)-(A.12).
to be
used later in Eqs. (A.10)-(A.12).
The curvature
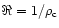 of the field lines (where
of the field lines (where
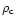 is
the radius of curvature presented for various cases in Figs. 2-8)
is calculated as
is
the radius of curvature presented for various cases in Figs. 2-8)
is calculated as
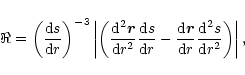 |
(A.8) |
where
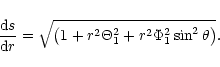 |
(A.9) |
Thus, the curvature can be written in the form
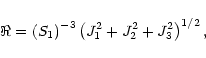 |
(A.10) |
where
| J1 |
= |
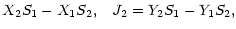 |
|
| J3 |
= |
Z2S1-Z1S2 |
|
| X1 |
= |
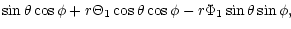 |
|
| Y1 |
= |
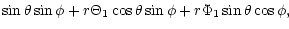 |
|
| Z1 |
= |
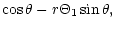 |
|
| X2 |
= |
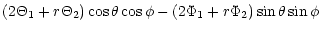 |
|
| |
|
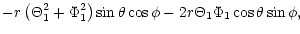 |
|
| Y2 |
= |
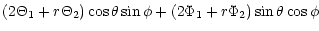 |
|
| |
|
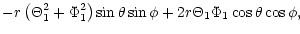 |
|
| Z2 |
= |
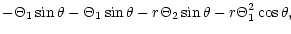 |
|
| S1 |
= |
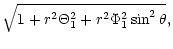 |
|
| S2 |
= |
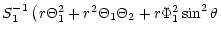 |
|
| |
 |
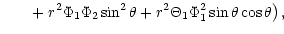 |
|
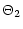 |
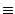 |
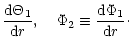 |
(A.11) |
In the two-dimensional case Eq. (A.8) can be simplified to
the following form
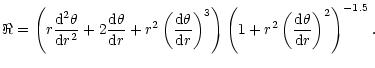 |
|
|
(A.12) |
Acknowledgements
This paper is supported in part by the KBN Grant 2 P03D 008 19 of
the Polish State Committee for Scientific Research. We are
grateful to Dr. U. Geppert for very helpful discussions. We also
thank E. Gil and G. Melikidze Jr. for technical help. DM would
like to thank the Institute of Astronomy, University of Zielona
Góra, for support and hospitality during his visit to the
institute, where this and the accompanying paper were
started.


Up: Modelling of the surface
Copyright ESO 2002
![]() and
the crust-anchored dipole moment
and
the crust-anchored dipole moment ![]() ,
let us consider the
general geometrical situation presented in Fig. 1. The
resultant surface magnetic field is
,
let us consider the
general geometrical situation presented in Fig. 1. The
resultant surface magnetic field is
![]() have a well known form in spherical
co-ordinates
have a well known form in spherical
co-ordinates
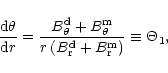
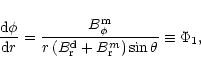
![]() of the field lines (where
of the field lines (where
![]() is
the radius of curvature presented for various cases in Figs. 2-8)
is calculated as
is
the radius of curvature presented for various cases in Figs. 2-8)
is calculated as