The geometry and internal structure of the bow shock nebula resulting from our simulations are shown in Figs. 1 and 2, while a grey-scale contour plot of the density is shown in Fig. 3. The positions of the termination shock, bow shock and contact discontinuity do not change among the above mentioned simulations, and also the position of the sonic point remains essentially the same. This is because the solution, in the hypersonic limit, depends only on the ratio between ram pressures of the stellar and ambient medium, but not separately on their densities or velocities: therefore we are confident that we have approximated well the hypersonic limit. The dashed lines represent three analytic solutions (Wilkin 1996), one scaled to match the contact discontinuity near the head, one to match the bow-shock near the head, and the long-dashed one, which is evaluated for the correct wind/environment ram pressure ratio. It can be seen that the analytic model reproduces quite well the shape of the nebula, although an uncertainty remains in the size. Figure 1 shows that the region of unperturbed stellar wind extends in the tail up to a "spherical shock'', whose position is strictly connected to the value of the thermal pressure in the ambient medium. In fact in the tail the pressure tends to the values of the ambient medium ![]() so the distance of the spherical shock can be easily derived as:
so the distance of the spherical shock can be easily derived as:
We remark that the outflow boundaries we use may introduce spurious waves, and this plays a role in the structure of the subsonic region (region A) especially as it may change the position of the triple point (where the spherical shock meets the termination shock). However the head of the simulated nebula, and the supersonic region of the external shocked layer are not affected, so that the following comparison with the analytic model is still valid.
Looking at the head (Fig. 2) we notice a bump in the contact discontinuity, due to an instability that has not been damped completely by diffusion. The contact discontinuity in the tail (Figs. 1 and 3) tends to reach a limiting distance from the axis (i.e. the shocked pulsar wind is confined to a cylinder), with radius of the same order of the stagnation point distance; instead, the external bow-shock tends to reach the Mach cone.
An upper limit to the radius of the contact discontinuity can be evaluated using an asymptotic treatment. Asymptotically in the tail the bow shock degenerates in a Mach cone, so the pressure in the external layer is essentially the same as the thermal pressure of the ambient medium ![]() .
Inside the contact discontinuity there are two different regions: the innermost (labeled as region A) corresponds to the material shocked in the spherical shock, which moves subsonically; the other region (region B), which surrounds the previous one, is filled with the material which crossed the termination shock at distances from the pulsar less than the spherical shock. As shown in Figs. 1 and 2, the material in the latter region moves supersonically. In a steady state model the pressure in these two regions must asymptotically match the conditions in the ambient medium. So the pressure inside the contact discontinuity is also
.
Inside the contact discontinuity there are two different regions: the innermost (labeled as region A) corresponds to the material shocked in the spherical shock, which moves subsonically; the other region (region B), which surrounds the previous one, is filled with the material which crossed the termination shock at distances from the pulsar less than the spherical shock. As shown in Figs. 1 and 2, the material in the latter region moves supersonically. In a steady state model the pressure in these two regions must asymptotically match the conditions in the ambient medium. So the pressure inside the contact discontinuity is also ![]() and this justifies Eq. (4) for the position of the spherical shock.
and this justifies Eq. (4) for the position of the spherical shock.
If we consider a fluid particle moving in region B, from a position near the stagnation point (labeled with subscript
![]() )
towards the asymptotic region in the tail (labeled with subscript
)
towards the asymptotic region in the tail (labeled with subscript
![]() ), the entropy conservation requires:
), the entropy conservation requires:
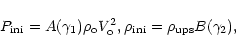 |
(6) |
| = | 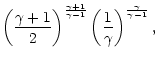 |
||
| = | 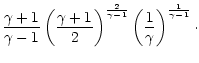 |
(7) |
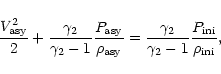 |
(9) |
The distance of the bow-shock from the star given by the analytic model is 0.175 Ul (long-dashed line) while the two limiting analytic solutions of Figs. 1 and 2 (dashed lines) are at 0.22 and 0.29 Ul. So the analytic model for the correct wind/environment ram pressure ratio gives a value which corresponds to the termination shock, while the thickness of the external layer is 0.025 Ul, in good agreement with what was expected (Paper I). Even though the shocked layers of the nebula are not thin at all, we see that the analytic solution reproduces quite well the morphology, at least of the external layer, which corresponds to the H![]() emitting region. In the tail simulation we see that the contact discontinuity has not reached the asymptotic regime, its distance from the axis being less than the maximum value given by Eq. (11).
emitting region. In the tail simulation we see that the contact discontinuity has not reached the asymptotic regime, its distance from the axis being less than the maximum value given by Eq. (11).
The behaviour of the fluid in regions A and B may affect the synchrotron emission from the relativistic electrons and positrons coming from the pulsar and shocked in the termination shock. As we can see from Fig. 1, material flowing in region B becomes supersonic soon in the head. In a relativistic case, the Lorentz factor associated with the bulk motion of the fluid in the tail becomes greater than the Lorentz factor associated with the thermal motion of relativistic particles. If particles have relativistic motions their synchrotron emission can be detected only if their pitch angle is close to the observer direction. In the tail the relativistic bulk motion produces a beaming of the emission in the backward direction, so that the synchrotron emission from relativistic particles, in the case of a direction of observation perpendicular to the pulsar velocity direction, can be detected only in the head, while it fades in the tail. This holds true for the less energetic particles responsible for the radio emission and may even be true for those responsible for the X-ray emission. In region A the flow is subsonic, so the radio and X-ray emission can be detected. In this case we expect a cylindrical emitting region. If the spherical shock is far from the pulsar it may occur that the number of high energy particles confined in region A is so small that their emission might be under the threshold of detection, so that this region can be observed only in the radio band.
Using the numerical hydrodynamic solutions described above we have also evaluated the behaviour of a toroidal magnetic field wound around the symmetry axis and passively advected by the fluid. We considered the case of a pulsar wind with the energy associated with the ordered magnetic field much smaller than the ram pressure of the relativistic particles, and with the ratio between the two being independent of the direction. The value of such a field increases in the head, due to the compression in the termination shock, ranging from 7 times its upstream value, right after the shock, up to a factor of 30-35 with respect to its upstream value, near the contact discontinuity. In the tail it tends to decrease with respect to its value in the head due to the subsequent expansion of the fluid until it approaches a constant value:
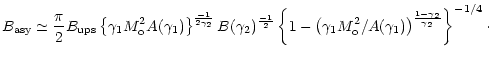 |
(12) |
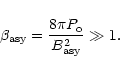 |
(13) |
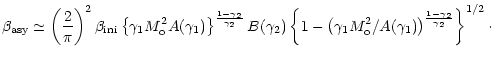 |
(14) |
To verify that the two thin layer model could be taken as a reasonable approximation of the true structure of the nebula, at least as far as the external layer is concerned, and to evaluate how far in the tail it could be used, we have extracted from our simulations the surface density and the tangential velocity in the external layer, between the bow shock and the contact discontinuity.
Figure 4 compares the surface density in the external layer, extracted from the tail simulation, with that evaluated by a two thin layer model. The numerical values have been obtained by integrating in the direction perpendicular to the bow shock. The difficulty in determining how good the analytic model approximation is follows from the fact that the analytic model depends on just one parameter, while the real problem has intrinsically two length scales (the stagnation point distance and the thickness in the head). In fact we have found two limit solutions (see Figs. 1 and 2), so that we could put only an upper and a lower limit to the length scale that should be used in the analytic model. The analytic curve that best reproduces the numerical points gives an external density of 0.26 cm-3 (instead of the true value 0.25 cm-3) and a stagnation point distance of 0.235 Ul, compatible with the range of the two limit solutions. The fluctuations of the numerical points are caused by round-off errors and uncertainties in the evaluation of the proper orthogonal direction, due to small oscillations in the shape of the bow shock, caused by discretisation errors in the evaluation of bow-shock position, eventually enhanced by the interpolation routine we use to find the orthogonal direction. In the simulation of the head we have noticed that, near the axis, the density values are lower than expected, and this effect corresponds to the bump of the contact discontinuity, that we have previously discussed. If corrected for the presence of the bump also in this zone we find reasonable values for the density.
In the same way, we have evaluated the tangential velocity in the layer between the bow shock and the contact discontinuity. Figure 5 shows the numerical values of the tangential velocity in the external layer, normalized to the external wind value, and compares it to the two thin layer model. The analytic curve that reproduces the points has been obtained using a value of 0.25 Ul for the distance of the stagnation point, a value in agreement with the two limit solutions. The fluctuations in the numerical points are much smaller than those seen in the surface density, which implies that the velocity pattern is more uniform in the layer with respect to the density.
The fact that the analytic curves that best reproduce the numerical values correspond to different values of the stagnation point distance tells us that the density and velocity cannot be reproduced exactly by the same thin layer model. It should be stressed, though, that, in spite of the non-thin structure of the external layer, the thin layer model is not a bad approximation. Deviations from the continuous curves are present only in the tail where a steady state regime may have not been achieved yet.
Copyright ESO 2002