To simulate a spherically symmetric wind from a moving star, interacting with the ambient medium, we have used the multi-D code CLAWPACK (LeVeque 1994): a second order Godunov (Godunov 1959) with piecewise linear reconstruction and transverse flux corrections. The problem has an intrinsic cylindrical symmetry which allows us to use a two-dimensional grid with Strang Splitting (Strang 1968) for the geometrical terms. The boundary conditions we have imposed are: 1. At every time step the values of all relevant quantities inside a sphere of given radius centered on the star are reset to the free flowing solution; 2. A uniform wind enters the computational box from the right hand side. We have put reflecting conditions on the axis of symmetry. On the left hand side of the box there is a free outflow boundary condition: all values of variables in the ghost zones are equal to the values in the corresponding active zones (extrapolating the flow beyond the boundary), taking care to avoid the possible inflow of material due to roll-up features (Stone & Norman 1992; LeVeque et al. 1997). This boundary condition, despite its simplicity, works quite well, and is actually used by various codes. We know from solar-wind simulations that the choice of such boundary conditions may influence the evolution in the case of subsonic outflow, but even in more sophisticated codes, the only way to solve the problem seems to take boundaries very far from the zone of interest (Pauls et al. 1995). We have tested the code with our simple boundary, and we have found that there are no significant problems with reflected spurious waves, and even following the evolution of our simulations we do not find spurious wave. Both the stellar and the external winds are taken with high Mach numbers (hypersonic limit). In fact the pulsar wind has a thermal pressure much lower than its ram pressure and the same holds true for the ISM, because pulsars have typical peculiar velocities of 200 km s-1 (Cordes & Chernoff 1998) while the typical temperature of the ISM is of the order of 104-105 K.
The pulsar wind is highly relativistic, with a Lorentz factor up to 106 (Rees & Gunn 1973; Kennel & Coroniti 1984), thus in order to handle it properly a relativistic code is required; however the geometry of such nebulae is essentially determined by the momentum flux of the winds (Wilkin 1996), so even a classical model can give a reasonable approximation. We decided to use a different adiabatic coefficient for the pulsar wind material and the ambient medium, so we have modified the Roe Riemann Solver (Roe 1981) used by the code, adding a tracer ![]() to separate the ambient medium (with adiabatic coefficient
to separate the ambient medium (with adiabatic coefficient
![]() )
from the relativistic (with
)
from the relativistic (with
![]() )
fluid coming from the star (Shyue 1998; Karni 1994). We then integrate the set of equations:
)
fluid coming from the star (Shyue 1998; Karni 1994). We then integrate the set of equations:
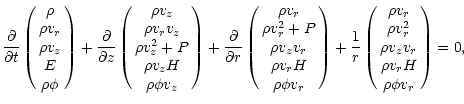 |
(2) |
 |
(3) |
The unit length we have used, Ul, has the value 1016 cm, chosen to reproduce typical pulsar bow-shock nebula dimensions (Eq. (1)). The simulations of the head were performed on a 0.40
![]() Ul box, using a grid of
Ul box, using a grid of
![]() cells with the star located in (100, 0). For the simulations of the tail, we used a 1.45
cells with the star located in (100, 0). For the simulations of the tail, we used a 1.45
![]() Ul box with a grid of
Ul box with a grid of
![]() cells and the star in (420, 0). The stellar wind has a velocity of 1000 km s-1, a density of 0.04 cm-3 and a Mach number of about 13 upstream of the termination shock along the bow shock axis. We have performed various simulations using different velocities for the external flow (400, 300, 200, 150 km s-1) and densities varying accordingly, in order to keep the ram pressure constant. The following figures refer to the simulation of 400 km s-1 (density of 0.25 cm-3). The time needed to reach the steady state condition is of the order of 4-5 times the external flow crossing time in the computational box.
cells and the star in (420, 0). The stellar wind has a velocity of 1000 km s-1, a density of 0.04 cm-3 and a Mach number of about 13 upstream of the termination shock along the bow shock axis. We have performed various simulations using different velocities for the external flow (400, 300, 200, 150 km s-1) and densities varying accordingly, in order to keep the ram pressure constant. The following figures refer to the simulation of 400 km s-1 (density of 0.25 cm-3). The time needed to reach the steady state condition is of the order of 4-5 times the external flow crossing time in the computational box.
Copyright ESO 2002