In this paper we have explored in detail a method to obtain informations on the geometry of the Universe with gravitational lensing. It follows an approach first presented by Link & Pierce (LP98) which states that multiple imaging systems at different redshifts can provide constraints not only on the mass profile of the lensing cluster but also on second order parameters like $\Omega _m$ or $\Omega _\lambda$ - contained in angular size distances ratios. We have shown that this technique gives constraints which are degenerate in the $(\Omega _m, \Omega _\lambda )$ plane and that the degeneracy is roughly perpendicular to the degeneracy issued from high-redshift supernovae searches. Moreover, the matter density $\Omega _m$ can be better constrained than the $\Lambda$ -term. Several simulations of lensing configurations are proposed, assuming reasonable conditions on the cluster-lens potential, such as a regular morphology modeled with only a few parameters. Provided high quality data can be obtained on at least 3 systems of multiple images, such as high resolution images (HST-type) for accurate image positions and deep spectroscopic data for the measurement of the source redshifts, we can expect typical error bars of $\Omega_m=0.30~\pm ~0.11$ , $\Omega_\lambda=0.70 \ \pm 0.23$ .

Table 6: List of 6 redshift configurations used in the combination of different cluster-lenses (Fig. 18) for a global $\chi ^2$ minimisation.
$z_{\rm L}$ $z_{\rm S1}$ $z_{\rm S2}$ $z_{\rm S3}$

0.15 0.4 0.8 2.0

0.2 0.5 1.0 3.0

0.25 0.6 0.9 2.0

0.3 0.6 1.0 2.0

0.35 0.6 1.5 3.0

0.4 0.8 1.8 4.0

**Table 6:** List of 6 redshift configurations used in the combination of different cluster-lenses (Fig. 18) for a global $\chi ^2$ minimisation.
$z_{\rm L}$	$z_{\rm S1}$	$z_{\rm S2}$	$z_{\rm S3}$
0.15	0.4	0.8	2.0
0.2	0.5	1.0	3.0
0.25	0.6	0.9	2.0
0.3	0.6	1.0	2.0
0.35	0.6	1.5	3.0
0.4	0.8	1.8	4.0

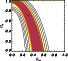$\begin{figure} \par\resizebox{\hsize}{!}{\includegraphics{MS1282f18.ps}}\end{figure}$

Figure 18: Color scale: $\chi ^2(\Omega _m,\Omega _\lambda )$ confidence levels obtained for a combination of 6 different cluster-lenses configurations (see Table 6 for redshift informations). The 3 main cluster parameters $\sigma _0$ , $\theta _a$ , $\theta _s$ were recovered for each cluster with a reduced $\chi ^2_{\rm min}=0$ and $\nu =60$ degrees of freedom. Dark to light colors delimit the confidence levels (from 1- $\sigma$ to 4- $\sigma$ ). Solid lines: $\chi ^2$ confidence levels (from 1- $\sigma$ to 4- $\sigma$ ) obtained for a single cluster at $z_{\rm L} = 0.3$ (same as Fig. 7). The cross (+) represents the original values $(\Omega _m^0,\Omega _\lambda ^0)=(0.3,0.7)$ .

It is important to underline that one cluster-lens with adequate multiple images would provide by itself a strong constraint on the geometry of the whole Universe. Such clusters are not that rare: MS2137.3-2353, MS0440.5+0204, A370, A1689, A2218, AC114 are certainly good candidates for such an experiment. A thorough and detailed analysis is still to be done and we have in hand most of the tools to address the problem immediately. Furthermore, as the exact degeneracy in the ( $\Omega _m$ , $\Omega _\lambda$ ) plane depends only on the values of the different redshift planes involved, combining results from different cluster-lenses can tighten the error bars. For illustration, we combined 6 different lens configurations and source redshifts, as listed in Table 6. Compared to the expected results with a single cluster (solid lines), the constraints can be improved significantly (Fig. 18).

Looking for a good accuracy on the cosmological parameters is a permanent search in cosmology. Although the curvature is now determined with a remarkable precision thanks to recent results from CMB balloon experiments, it is still very difficult to disentangle $\Omega _m$ from $\Omega _\lambda$ (Zaldarriaga et al. 1997). Therefore the advantages of joint analyses by several independent approaches have been pointed out (see White 1998 and Efstathiou et al. 1999): combined results from the m-z relation for SNIa and CMB power spectrum analyses (which have orthogonal degeneracies) constrain $\Omega _m$ or $\Omega _\lambda$ separately with much higher accuracy than the individual experiments alone, leading to the currently favored model. One impressive example has been given by Hu & Tegmark (1999) who showed that a relatively small weak lensing survey could dramatically improve the accuracy of the cosmological parameters measured by future CMB missions.The combination of independent tests can improve the constraints as well as serve as a consistency check. This is clearly demonstrated by Helbig et al. (1999) who combine constraints from lensing statistics and distant SNIa to get a narrow range of possible values for $\Omega _\lambda$ . Therefore, gravitational lensing is a powerful complementary method to address the determination of the geometrical cosmological parameters and probably one of the cheapest ones, compared to CMB experiments or SNIa searches. Our technique, when applied to about 10 clusters, should be included in such joint analysis, to obtain a consistent picture on the present cosmological parameters. We are truly entering an era of accurate cosmology, where the overlap between the allowed regions of parameter space is becoming quite reduced.

4 Conclusion and future prospects