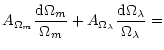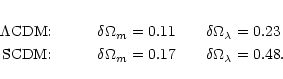Up: Constraining the cosmological parameters
Subsections
We first define the basic mathematical framework, following the
formalism presented in Schneider et al. (1992). We consider a lens at a
redshift 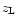 with a two-dimensional projected mass distribution
with a two-dimensional projected mass distribution
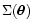 and a projected gravitational potential
and a projected gravitational potential
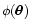 ,
where
,
where
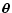 is a two-dimensional vector
representing the angular position. A source galaxy with redshift
is a two-dimensional vector
representing the angular position. A source galaxy with redshift 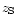 is located at position
is located at position
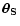 in the absence of a lens, and
its image is at position
in the absence of a lens, and
its image is at position
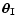 .
In the lens equation
.
In the lens equation
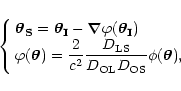 |
(1) |
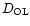 ,
,
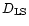 and
and
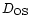 are
respectively the angular diameter
distances from the Observer to the Lens, from the Lens to the Source
and from the Observer to the Source (Peebles 1993).
are
respectively the angular diameter
distances from the Observer to the Lens, from the Lens to the Source
and from the Observer to the Source (Peebles 1993). 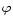 is the reduced
gravitational potential which satisfies
is the reduced
gravitational potential which satisfies
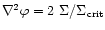 with the critical density
with the critical density
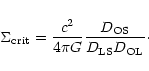 |
(2) |
In these equations the dependence on the cosmological parameters
appears only through the angular diameter distances ratios
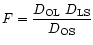 and
and
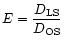 (E as "efficiency'') for a fixed cluster redshift. They correspond to a
scaling of the lens equation, reflecting the geometrical properties of
the Universe.
(E as "efficiency'') for a fixed cluster redshift. They correspond to a
scaling of the lens equation, reflecting the geometrical properties of
the Universe.
In the general case, we can scale the potential gradient as:
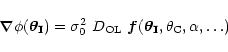 |
(3) |
where 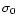 is the central velocity dispersion and
is the central velocity dispersion and 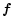 a
dimensionless function that describes the mass distribution of the
cluster. It can be represented by fiducial parameters such as a core
radius
a
dimensionless function that describes the mass distribution of the
cluster. It can be represented by fiducial parameters such as a core
radius
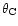 or a mass profile gradient
or a mass profile gradient 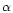 .
The lens
equation reads
.
The lens
equation reads
We will focus on the E-term which entirely contains the dependence
on 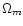 and
and
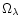 and which is independent of H0.
and which is independent of H0.
For a given lens plane 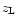 ,
the ratio E increases rapidly as the
source redshift increases, and then flattens at
,
the ratio E increases rapidly as the
source redshift increases, and then flattens at
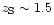 .
There are also small but significant changes with the cosmological
parameters (Fig. 2). The dependence of E with respect to
.
There are also small but significant changes with the cosmological
parameters (Fig. 2). The dependence of E with respect to
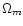 is weak, whereas the variation with
is weak, whereas the variation with
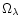 is
larger.
is
larger.
We now consider fixed redshifts for the lens and sources. Assuming a fixed
world model, a single
family of multiple images can in principle constrain the total cluster
mass as well as the shape of the potential, removing the unknown position
of the source
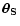 using Eq. (4).
In practice, good constraints on the shape of the potential
using Eq. (4).
In practice, good constraints on the shape of the potential 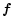 are obtained with triple, quadruple or quintuple image systems. However
the absolute normalization
are obtained with triple, quadruple or quintuple image systems. However
the absolute normalization
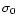 of the mass is degenerate with the E-term, that is with
respect to
of the mass is degenerate with the E-term, that is with
respect to 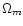 and
and
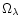 .
.
 |
Figure 2:
Variation of the lens efficiency
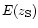 as a function of
the source redshift
for different sets of cosmological parameters. Left:
as a function of
the source redshift
for different sets of cosmological parameters. Left:
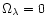 and
and 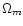 varies from 0.1 to 1.0.
Right:
varies from 0.1 to 1.0.
Right:
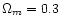 and
and
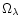 varies from 0 to
0.7. In both cases, the lens redshift is
varies from 0 to
0.7. In both cases, the lens redshift is
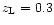 .
For clarity,
above each main plot, we also plotted the same curves, normalised with
the .
For clarity,
above each main plot, we also plotted the same curves, normalised with
the
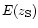 function for
function for
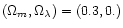 . .
|
2.3 Ratio of E-terms for 2 sets of source redshifts
To break this degeneracy a second family of multiple images is needed.
To get rid of the strong dependence on 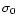 ,
it is useful to
consider the ratio of the positions:
,
it is useful to
consider the ratio of the positions:
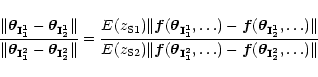 |
(5) |
(here and hereafter, the
superscript refers to a family and the subscript to a particular image
within a family). This ratio is plotted in Fig. 1, highlighting
the influence of 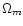 and
and
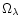 through the ratio
through the ratio
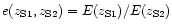 .
.
Note that the discrepancy between the different cosmological parameters is not
very large, less than 3% between the Einstein-de Sitter model (EdS)
and a flat, low matter density one. Moreover, a
characteristic degeneracy appears in the
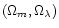 plane,
which is roughly orthogonal to the one given by the detection of high
redshift supernovae, and quite different from the CMB constraints.
A similar degeneracy was also found in the analog weak lensing analyses,
(Lombardi & Bertin 1999) or by Gautret et al. (2000).
plane,
which is roughly orthogonal to the one given by the detection of high
redshift supernovae, and quite different from the CMB constraints.
A similar degeneracy was also found in the analog weak lensing analyses,
(Lombardi & Bertin 1999) or by Gautret et al. (2000).
Another approach to quantify the dependence of a given lens configuration on
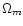 and
and
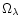 is to fix the lens redshift and to
search for two source redshifts
is to fix the lens redshift and to
search for two source redshifts
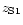 and
and
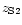 which give
the largest variation of the E-term when scanning the
which give
the largest variation of the E-term when scanning the
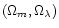 plane. For illustration we arbitrarily choose two
sets of cosmological parameters, for which the relative variation of Eis large: CP1
plane. For illustration we arbitrarily choose two
sets of cosmological parameters, for which the relative variation of Eis large: CP1
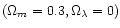 and CP2 (
and CP2 (
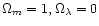 ,
i.e. the EdS model). Varying
,
i.e. the EdS model). Varying
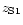 and
and
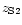 ,
the function
,
the function
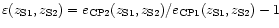 represents the percentage of discrepancy between CP1 and CP2 for
represents the percentage of discrepancy between CP1 and CP2 for
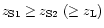 (Fig. 3).
(Fig. 3).
For a given high-redshift
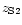 source the best lowest source
redshift is
source the best lowest source
redshift is
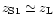 ,
and for a given
,
and for a given
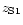 the best
the best
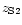 is the highest redshift, the difference between cosmological models
increasing with
is the highest redshift, the difference between cosmological models
increasing with
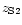 .
In all cases, this relative
difference is of the order of a few %, meaning that the lens mass
distribution must be known
to the same degree of accuracy to get further constraints
on the cosmological parameters. Hence, for 2 systems of images, the best
configuration is one background source close to the lens, in the
rising part of
.
In all cases, this relative
difference is of the order of a few %, meaning that the lens mass
distribution must be known
to the same degree of accuracy to get further constraints
on the cosmological parameters. Hence, for 2 systems of images, the best
configuration is one background source close to the lens, in the
rising part of
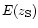 and another one at high redshift, to
take into account the asymptotic value of the ratio. Note however that for
a source redshift close to the lens, the E-term becomes very small.
Also, the location of the images is very close to the lens center which makes
the detection of multiple images quite improbable, as small caustic
sizes imply small cross sections.
and another one at high redshift, to
take into account the asymptotic value of the ratio. Note however that for
a source redshift close to the lens, the E-term becomes very small.
Also, the location of the images is very close to the lens center which makes
the detection of multiple images quite improbable, as small caustic
sizes imply small cross sections.
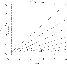 |
Figure 3:
Relative difference between the ratio
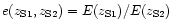 for two extreme cosmological models:
for two extreme cosmological models:
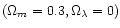 and (
and (
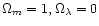 ). This function ). This function
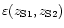 is
plotted in the
is
plotted in the
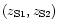 plane, assuming
plane, assuming
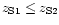 and
and
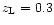 . . |
2.4 Relative influence of the lens parameters
In order to quantify the expected uncertainties on 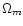 and
and
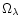 ,
it is possible to analytically estimate the
influence of the different lens models parameters. We use a
model of the potential derived from the mass density described by
Hjorth & Kneib (2001), hereafter HK. It is based on a physical scenario of
violent relaxation in galaxies, also valid in clusters of galaxies.
The mass density is characterized by a core radius a and a cut-off
radius s:
,
it is possible to analytically estimate the
influence of the different lens models parameters. We use a
model of the potential derived from the mass density described by
Hjorth & Kneib (2001), hereafter HK. It is based on a physical scenario of
violent relaxation in galaxies, also valid in clusters of galaxies.
The mass density is characterized by a core radius a and a cut-off
radius s:
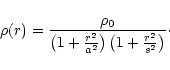 |
(6) |
Then the projected mass density
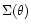 is represented by:
is represented by:
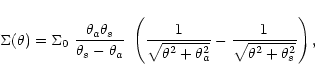 |
(7) |
where 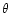 is the angular coordinate,
is the angular coordinate,
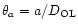 and
and
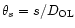 .
.
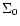 is a normalization factor,
related to the cluster parameters:
is a normalization factor,
related to the cluster parameters:
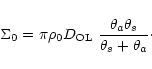 |
(8) |
Finally, the mass inside the projected angular radius 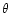 is:
is:
![$\displaystyle M(\theta) = 2\pi\Sigma_0 D_{\rm OL}^2 \
\frac{\theta_a\theta_s}{\...
...sqrt{\theta^2+\theta_a^2}-\sqrt{\theta^2+\theta_s^2}+
\theta_s-\theta_a\right].$](/articles/aa/full/2002/21/aa1282/img125.gif) |
|
|
(9) |
The velocity dispersion
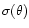 is related to the mass
density and the gravitational potential via the Jeans equation.
Assuming an isotropic velocity dispersion and retaining terms up to
first order in
is related to the mass
density and the gravitational potential via the Jeans equation.
Assuming an isotropic velocity dispersion and retaining terms up to
first order in
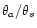 ,
we get the relation between the
central velocity dispersion
,
we get the relation between the
central velocity dispersion
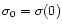 and
and 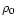 :
:
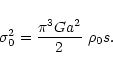 |
(10) |
Finally we compute the expression of the deviation angle between the
positions of the source and of the image due to the lens:
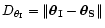 ,
neglecting
second order terms in
,
neglecting
second order terms in
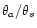 (we suppose here
(we suppose here 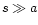 ):
):
![\begin{displaymath}D_{\theta_{\rm I}}\! =\! \frac{16}{\pi}\frac{\sigma_0^2}{c^2}...
..._a^2}
-\sqrt{\theta^2+\theta_s^2}+ \theta_s-\theta_a\right]\!.
\end{displaymath}](/articles/aa/full/2002/21/aa1282/img133.gif) |
(11) |
The central velocity dispersion (or equivalently the mass
normalization of the cluster core) is obviously the predominant factor
in any lens configuration. With a single family of images we can only
constrain the combination
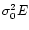 and cannot disentangle the
influence of the cosmological parameters and the absolute normalization
of the mass (Fig. 4). If we were able to measure the total
mass within the Einstein radius independently from lensing techniques
and with an accuracy better than a few %, we could in principle put
some constraints on
and cannot disentangle the
influence of the cosmological parameters and the absolute normalization
of the mass (Fig. 4). If we were able to measure the total
mass within the Einstein radius independently from lensing techniques
and with an accuracy better than a few %, we could in principle put
some constraints on
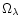 .
Observationally, there are 2
situations where it is likely that we could disentangle the
effect of cosmology and absolute mass:
.
Observationally, there are 2
situations where it is likely that we could disentangle the
effect of cosmology and absolute mass:
1) in the case of a cluster-lens with extremely good X-ray
data, particularly in estimating the temperature distribution of the gas
(under the assumption of hydrostatic equilibrium),
2) in the case of a multiple system around a single galaxy, for which
one is able to measure accurately the stellar velocity dispersion of
the lensing galaxy (Tonry & Franx 1999).
However in both cases this
represents some observational challenge and requires the most
powerful instruments to achieve this goal.
 |
Figure 4:
Variation of the central velocity dispersion 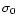 in the
(
in the
(
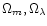 )
plane, assuming that the product )
plane, assuming that the product
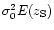 is constant.
is constant. 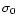 has been fixed to 1000
km s-1 for
has been fixed to 1000
km s-1 for
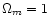 , ,
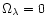 while
while
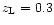 and
and
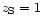 . .
|
Although the error budget in the image positions is dominated by the
error on the total cluster mass (or equivalently the velocity
dispersion), we can determine the relative influence of the other
parameters to infer the importance of 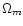 and
and
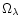 in the image formation. The relative error on the deviation angle
in the image formation. The relative error on the deviation angle
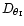 depends on
depends on 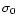 ,
,
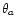 ,
,
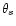 and
and
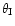 for the gravitational potential, and
for the gravitational potential, and 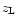 ,
,
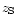 ,
,
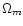 and
and
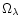 for the E-term (Eq. (11)).
Therefore we can
write:
for the E-term (Eq. (11)).
Therefore we can
write:
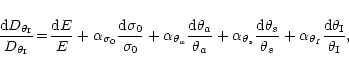 |
(12) |
with
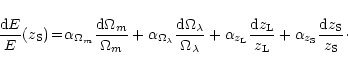 |
(13) |
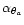 ,
,
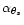 and
and
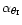 can
be computed analytically while
can
be computed analytically while
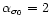 is the largest
factor. Since the angular diameter distances do not have an analytic
expression if
is the largest
factor. Since the angular diameter distances do not have an analytic
expression if
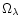 is non-zero, the coefficients
is non-zero, the coefficients
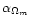 ,
,
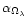 ,
,
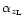 and
and
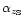 must be computed numerically. In practise, they are
computed for a given set of parameters
must be computed numerically. In practise, they are
computed for a given set of parameters
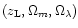 as their variation with
as their variation with 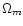 and
and
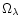 is of higher order. For a reasonable set of lens
parameters, the
is of higher order. For a reasonable set of lens
parameters, the 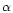 -coefficients are of the same order of
magnitude, except that
-coefficients are of the same order of
magnitude, except that
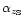 and
and
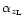 can dominate
the error budget if the source redshift is close to the lens (an unlikely
case). On the contrary,
can dominate
the error budget if the source redshift is close to the lens (an unlikely
case). On the contrary,
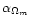 and
and
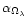 are
of second order, and
are
of second order, and
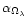 is somewhat larger than
is somewhat larger than
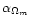 .
This reflects again the fact that E-term is
more sensitive to
.
This reflects again the fact that E-term is
more sensitive to
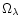 than to
than to 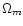 .
.
To quantify the relative influence of all the parameters in the case
of a single family of images, we computed explicitely
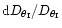 in two cases, for a cluster-lens and for
a galaxy-lens.
in two cases, for a cluster-lens and for
a galaxy-lens.
1) For a cluster of galaxies, we take the following parameters:
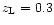 ,
,
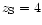 ,
,
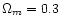 ,
,
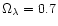 ,
,
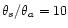 and
and
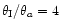 .
We thus find from Eq. (11):
.
We thus find from Eq. (11):
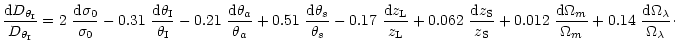 |
|
|
(14) |
Let us assume a perfectly known mass profile (i.e. d
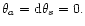 ). Neglecting the influence of
). Neglecting the influence of 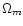 ,
we ask what precision
would be required on
,
we ask what precision
would be required on 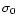 to derive an error of 50% on
to derive an error of 50% on
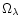 .
The accuracy of the position of the center of the images is calculated using
the first moment of the flux
.
The accuracy of the position of the center of the images is calculated using
the first moment of the flux 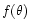 on a
given image:
on a
given image:
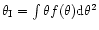 /
/
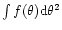 which yields an error
which yields an error
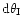 of a fraction
of the spatial resolution. HST observations are then required to reach
of a fraction
of the spatial resolution. HST observations are then required to reach
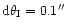 (LP98) or better. To reduce the
uncertainty on the
redshift measurements, we assume spectroscopic determinations, so that
d
(LP98) or better. To reduce the
uncertainty on the
redshift measurements, we assume spectroscopic determinations, so that
d
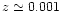 .
Finally we have to compute
the relative errors on
.
Finally we have to compute
the relative errors on
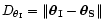 ,
so the position of the
source is in principle required. But as we are in the strong lensing
regime, we assume that
,
so the position of the
source is in principle required. But as we are in the strong lensing
regime, we assume that
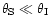 ,
so that both
quantities
,
so that both
quantities
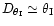 and
and
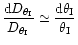 are directly related to
observable ones. Taking these values into account, we need to know
are directly related to
observable ones. Taking these values into account, we need to know 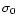 with 3.6% accuracy to get the expected constraint on
with 3.6% accuracy to get the expected constraint on
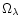 .
Such an accuracy is out of reach with observations of clusters of
galaxies.
.
Such an accuracy is out of reach with observations of clusters of
galaxies.
2) For a single galaxy, we consider typically:
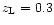 ,
,
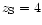 ,
,
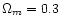 ,
,
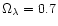 ,
,
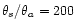 and
and
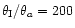 (ratios taken from the modelisation of the lens
HST 14176+5226 by Hjorth & Kneib 2001), leading to:
(ratios taken from the modelisation of the lens
HST 14176+5226 by Hjorth & Kneib 2001), leading to:
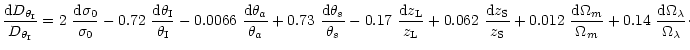 |
|
|
(15) |
Taking the same values for the observational errors and considering a
perfectly known mass
profile, we require an accuracy of 6.4% on 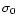 to
derive a 50% error on
to
derive a 50% error on
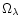 .
For a typical galaxy, this
represents
about 15 km s-1. Warren et al. (1998) measured the
velocity dispersion in the deflector of the Einstein ring
0047-2808 with an error of 30 km s-1.
A better accuracy could be obtained
by looking at particular strong absorption features with 10 m class telescope
observations. This could be sufficient to confirm an accelerating
Universe.
.
For a typical galaxy, this
represents
about 15 km s-1. Warren et al. (1998) measured the
velocity dispersion in the deflector of the Einstein ring
0047-2808 with an error of 30 km s-1.
A better accuracy could be obtained
by looking at particular strong absorption features with 10 m class telescope
observations. This could be sufficient to confirm an accelerating
Universe.
With a second system of multiple images another region of the
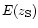 curve is probed while the cluster parameters are the same. In that case,
the relevant quantity becomes the ratio of the deviation angles for 2
images
curve is probed while the cluster parameters are the same. In that case,
the relevant quantity becomes the ratio of the deviation angles for 2
images
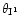 and
and
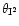 belonging to 2 different
families at redshifts
belonging to 2 different
families at redshifts
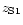 and
and
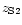 .
We define
.
We define
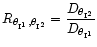 .
This function has the advantage that it does not
depend on
.
This function has the advantage that it does not
depend on 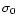 anymore. Following our previous definitions,
we can write
anymore. Following our previous definitions,
we can write
Numerically, we chose a typical configuration to compute
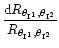 :
:
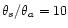 ,
,
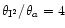 ,
,
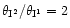 ,
,
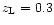 ,
,
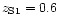 ,
,
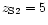 ,
assuming
,
assuming
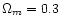 and
and
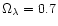 .
This gives the following error budget:
.
This gives the following error budget:
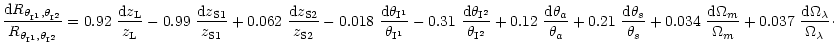 |
|
|
(17) |
The contribution of the physical lens parameters in this error budget
is strongly attenuated comprared to the single family case. There is no
more dependence on 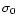 and
the dependence on the mass profile (
and
the dependence on the mass profile (
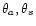 )
is reduced
by about a factor of 2 compared to a single family of images. This
corresponds to the variation of the potential between
)
is reduced
by about a factor of 2 compared to a single family of images. This
corresponds to the variation of the potential between
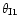 and
and
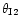 ,
the absolute normalization being removed. Anyhow,
this can still represent the main source of error because we cannot
expect to constrain
,
the absolute normalization being removed. Anyhow,
this can still represent the main source of error because we cannot
expect to constrain 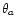 to better than 1.5% and
to better than 1.5% and 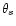 to
better than 2% typically (see Sect. 3.3.3).
to
better than 2% typically (see Sect. 3.3.3).
For the source redshifts, we have selected one of the sources at
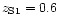 ,
which means that its
,
which means that its
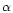 -coefficient is quite large. The accurate value of the
redshifts is thus fundamental, and a spectroscopic determination is
essential (d
-coefficient is quite large. The accurate value of the
redshifts is thus fundamental, and a spectroscopic determination is
essential (d
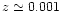 ). A photometric redshift estimate would
not be satisfactory, because we cannot expect an accuracy better than
10% in most cases (
). A photometric redshift estimate would
not be satisfactory, because we cannot expect an accuracy better than
10% in most cases (
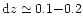 ,
Bolzonella et al. 2000). We
keep
,
Bolzonella et al. 2000). We
keep
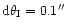 .
The strong lensing regime approximation
leads to
.
The strong lensing regime approximation
leads to
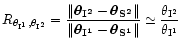 and
and
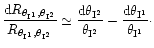
We can then separate the contributions of the parameters that do not
depend on 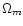 or
or
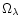 from those which depend on
them and re-write Eq. (16):
from those which depend on
them and re-write Eq. (16):
| |
|
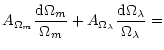 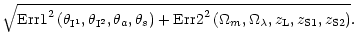 |
(18) |
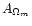 and
and
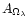 depend on
depend on
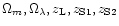 while Err12 and Err22 are
the quadratic sums of the errors, with a separation between the
geometrical parameters and those depending on the cosmology. For each
set of cosmological parameters we then compute all these coefficients
numerically. In addition, we also need a calculation of the
"degeneracy''
while Err12 and Err22 are
the quadratic sums of the errors, with a separation between the
geometrical parameters and those depending on the cosmology. For each
set of cosmological parameters we then compute all these coefficients
numerically. In addition, we also need a calculation of the
"degeneracy''
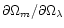 to obtain
either
to obtain
either
 or
or
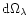 .
This is the
slope of the
degeneracy curves of the E-terms ratio plotted in Fig. 1.
Indeed considering 2 points
.
This is the
slope of the
degeneracy curves of the E-terms ratio plotted in Fig. 1.
Indeed considering 2 points
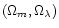 and
and
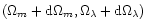 on
such a curve
(for a given set of
on
such a curve
(for a given set of 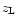 ,
,
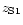 ,
,
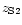 ), we have
), we have
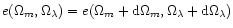 so that we get
so that we get
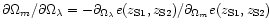 .
The final
expected errors on
.
The final
expected errors on
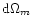 and
and
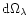 are
plotted in
Fig. 5 for a continuous set of world models. The
method is in general far more sensitive to the matter density than to
the cosmological constant, for which the error bars are larger. This
apparent contradiction with the general statement that lensing is more
sensitive to the cosmological constant than to the matter density is
due to the fact that we analysed the ratio of two E-terms and
this ratio varies more rapidly with
are
plotted in
Fig. 5 for a continuous set of world models. The
method is in general far more sensitive to the matter density than to
the cosmological constant, for which the error bars are larger. This
apparent contradiction with the general statement that lensing is more
sensitive to the cosmological constant than to the matter density is
due to the fact that we analysed the ratio of two E-terms and
this ratio varies more rapidly with 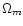 when scanning the
when scanning the
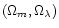 plane (Fig. 1). For
illustration, we quantitatively obtain the following errors for the
corresponding cosmological models:
plane (Fig. 1). For
illustration, we quantitatively obtain the following errors for the
corresponding cosmological models:
 |
Figure 5:
Final errors d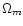 (left) and d
(left) and d
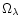 (right) for a given
(right) for a given
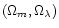 in the lens
configuration discussed in the text (Sect. 2.4), for
two source redshifts
in the lens
configuration discussed in the text (Sect. 2.4), for
two source redshifts
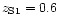 and
and
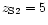 . .
|
This analysis shows that the expected results are quite encouraging,
and the constraints we could get are similar to the ones currently
obtained by other methods. Note however that these typical values
require both HST imaging of cluster lenses and deep spectroscopic
observations for the redshift determination of multiple arcs. They may
depend on the choice of the lens parameters and on the potential
model chosen to describe the lens, a problem that we will now investigate.


Up: Constraining the cosmological parameters
Copyright ESO 2002
![]() with a two-dimensional projected mass distribution
with a two-dimensional projected mass distribution
![]() and a projected gravitational potential
and a projected gravitational potential
![]() ,
where
,
where
![]() is a two-dimensional vector
representing the angular position. A source galaxy with redshift
is a two-dimensional vector
representing the angular position. A source galaxy with redshift ![]() is located at position
is located at position
![]() in the absence of a lens, and
its image is at position
in the absence of a lens, and
its image is at position
![]() .
In the lens equation
.
In the lens equation
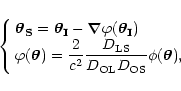
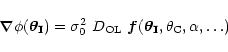
![]() using Eq. (4).
In practice, good constraints on the shape of the potential
using Eq. (4).
In practice, good constraints on the shape of the potential ![]() are obtained with triple, quadruple or quintuple image systems. However
the absolute normalization
are obtained with triple, quadruple or quintuple image systems. However
the absolute normalization
![]() of the mass is degenerate with the E-term, that is with
respect to
of the mass is degenerate with the E-term, that is with
respect to ![]() and
and
![]() .
.
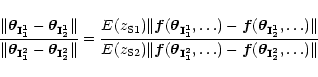
![]() plane,
which is roughly orthogonal to the one given by the detection of high
redshift supernovae, and quite different from the CMB constraints.
A similar degeneracy was also found in the analog weak lensing analyses,
(Lombardi & Bertin 1999) or by Gautret et al. (2000).
plane,
which is roughly orthogonal to the one given by the detection of high
redshift supernovae, and quite different from the CMB constraints.
A similar degeneracy was also found in the analog weak lensing analyses,
(Lombardi & Bertin 1999) or by Gautret et al. (2000).
![]() and
and
![]() is to fix the lens redshift and to
search for two source redshifts
is to fix the lens redshift and to
search for two source redshifts
![]() and
and
![]() which give
the largest variation of the E-term when scanning the
which give
the largest variation of the E-term when scanning the
![]() plane. For illustration we arbitrarily choose two
sets of cosmological parameters, for which the relative variation of Eis large: CP1
plane. For illustration we arbitrarily choose two
sets of cosmological parameters, for which the relative variation of Eis large: CP1
![]() and CP2 (
and CP2 (
![]() ,
i.e. the EdS model). Varying
,
i.e. the EdS model). Varying
![]() and
and
![]() ,
the function
,
the function
![]() represents the percentage of discrepancy between CP1 and CP2 for
represents the percentage of discrepancy between CP1 and CP2 for
![]() (Fig. 3).
(Fig. 3).
![]() source the best lowest source
redshift is
source the best lowest source
redshift is
![]() ,
and for a given
,
and for a given
![]() the best
the best
![]() is the highest redshift, the difference between cosmological models
increasing with
is the highest redshift, the difference between cosmological models
increasing with
![]() .
In all cases, this relative
difference is of the order of a few %, meaning that the lens mass
distribution must be known
to the same degree of accuracy to get further constraints
on the cosmological parameters. Hence, for 2 systems of images, the best
configuration is one background source close to the lens, in the
rising part of
.
In all cases, this relative
difference is of the order of a few %, meaning that the lens mass
distribution must be known
to the same degree of accuracy to get further constraints
on the cosmological parameters. Hence, for 2 systems of images, the best
configuration is one background source close to the lens, in the
rising part of
![]() and another one at high redshift, to
take into account the asymptotic value of the ratio. Note however that for
a source redshift close to the lens, the E-term becomes very small.
Also, the location of the images is very close to the lens center which makes
the detection of multiple images quite improbable, as small caustic
sizes imply small cross sections.
and another one at high redshift, to
take into account the asymptotic value of the ratio. Note however that for
a source redshift close to the lens, the E-term becomes very small.
Also, the location of the images is very close to the lens center which makes
the detection of multiple images quite improbable, as small caustic
sizes imply small cross sections.

![]() and
and
![]() ,
it is possible to analytically estimate the
influence of the different lens models parameters. We use a
model of the potential derived from the mass density described by
Hjorth & Kneib (2001), hereafter HK. It is based on a physical scenario of
violent relaxation in galaxies, also valid in clusters of galaxies.
The mass density is characterized by a core radius a and a cut-off
radius s:
,
it is possible to analytically estimate the
influence of the different lens models parameters. We use a
model of the potential derived from the mass density described by
Hjorth & Kneib (2001), hereafter HK. It is based on a physical scenario of
violent relaxation in galaxies, also valid in clusters of galaxies.
The mass density is characterized by a core radius a and a cut-off
radius s:
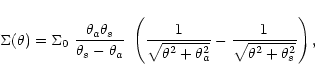
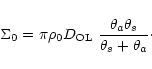
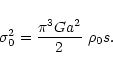

![]() and
and
![]() in the image formation. The relative error on the deviation angle
in the image formation. The relative error on the deviation angle
![]() depends on
depends on ![]() ,
,
![]() ,
,
![]() and
and
![]() for the gravitational potential, and
for the gravitational potential, and ![]() ,
,
![]() ,
,
![]() and
and
![]() for the E-term (Eq. (11)).
Therefore we can
write:
for the E-term (Eq. (11)).
Therefore we can
write:
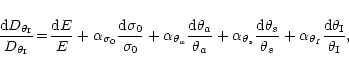
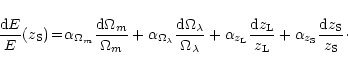
![]() in two cases, for a cluster-lens and for
a galaxy-lens.
in two cases, for a cluster-lens and for
a galaxy-lens.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
We thus find from Eq. (11):
.
We thus find from Eq. (11):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() (ratios taken from the modelisation of the lens
HST 14176+5226 by Hjorth & Kneib 2001), leading to:
(ratios taken from the modelisation of the lens
HST 14176+5226 by Hjorth & Kneib 2001), leading to:
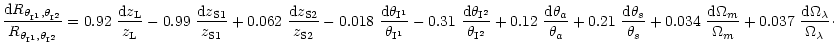
![]() ,
which means that its
,
which means that its
![]() -coefficient is quite large. The accurate value of the
redshifts is thus fundamental, and a spectroscopic determination is
essential (d
-coefficient is quite large. The accurate value of the
redshifts is thus fundamental, and a spectroscopic determination is
essential (d
![]() ). A photometric redshift estimate would
not be satisfactory, because we cannot expect an accuracy better than
10% in most cases (
). A photometric redshift estimate would
not be satisfactory, because we cannot expect an accuracy better than
10% in most cases (
![]() ,
Bolzonella et al. 2000). We
keep
,
Bolzonella et al. 2000). We
keep
![]() .
The strong lensing regime approximation
leads to
.
The strong lensing regime approximation
leads to
![]() and
and
![]()
![]() or
or
![]() from those which depend on
them and re-write Eq. (16):
from those which depend on
them and re-write Eq. (16):