

Up: A new determination of
3 The fitted parameters
We list below the parameters that are fit in the solutions S1998 and S2000.
All the angles and mean motions are referred to J2000.0.
- The geocentric lunar orbital parameters
W1(0),
W2(0),
W3(0) (constants of the mean
longitude and mean longitudes of perigee and node),
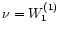 ,
,
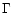 ,
E (sidereal mean motion, constants for inclination and
eccentricity).
,
E (sidereal mean motion, constants for inclination and
eccentricity).
- The heliocentric orbital parameters of the Earth-Moon barycenter
T(0),
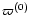 (constants of the mean longitude and mean
longitude of perihelion), n', e' (sidereal mean motion and eccentricity).
(constants of the mean longitude and mean
longitude of perihelion), n', e' (sidereal mean motion and eccentricity).
- The bias parameters
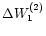 ,
,
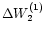 ,
,
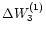 (observed corrections to the computed coefficient of the quadratic term of
the lunar mean longitude, and the computed mean motions of perigee
and node).
(observed corrections to the computed coefficient of the quadratic term of
the lunar mean longitude, and the computed mean motions of perigee
and node).
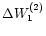 yields an observed value of
W1(2,T), the tidal
part of the coefficient of the quadratic term of the mean longitude (half
tidal secular acceleration).
yields an observed value of
W1(2,T), the tidal
part of the coefficient of the quadratic term of the mean longitude (half
tidal secular acceleration).
- The 6 free libration parameters
(parameters tied to the coefficients of the main free libration terms and
values of the free libration arguments).
- The 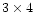 reflector coordinates.
The reflector coordinates are referred to lunar principal axes of inertia.
reflector coordinates.
The reflector coordinates are referred to lunar principal axes of inertia.
- The position angles
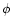 ,
,
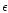 and
and 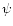 with respect to different systems of axes.
Figure 2 illustrates the relative positions of various systems
presented in Sect. 4.
with respect to different systems of axes.
Figure 2 illustrates the relative positions of various systems
presented in Sect. 4.
- A correction to precession 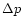 :
optional parameter.
:
optional parameter.
In the solution S2001 we keep the same list as above and we add
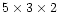 optional parameters giving the positions and velocities
of the 5 stations: McDONALD 2.70 m, MLRS1 and MLRS2, CERGA and Haleakala.
The parameters are the equatorial rectangular coordinates X, Y, Z in
the ITRF (position) and their derivatives
optional parameters giving the positions and velocities
of the 5 stations: McDONALD 2.70 m, MLRS1 and MLRS2, CERGA and Haleakala.
The parameters are the equatorial rectangular coordinates X, Y, Z in
the ITRF (position) and their derivatives 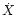 ,
,
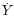 ,
,
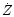 (velocity).
Note that simultaneously fitting all the parameters has not been possible.
The fits have been performed in several steps, but tests have been made in
order to check the stability of the results.
Indeed, strong correlations exist among some parameters that may weaken
the accuracy of our determinations; in particular, it is the case of the
variables related to the reference frame (
(velocity).
Note that simultaneously fitting all the parameters has not been possible.
The fits have been performed in several steps, but tests have been made in
order to check the stability of the results.
Indeed, strong correlations exist among some parameters that may weaken
the accuracy of our determinations; in particular, it is the case of the
variables related to the reference frame (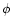 and
and 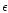 )
and the
positions of the stations (X, Y, Z).
)
and the
positions of the stations (X, Y, Z).
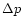 (precession) and
(precession) and
 (obliquity rate) are correlated
with the velocities of the stations (
(obliquity rate) are correlated
with the velocities of the stations (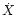 ,
,
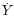 ,
,
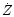 );
);
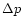 and the principal nutation term are also difficult
to separate.
We have adopted the following strategy. First, we determine the whole set
of parameters mentioned above except the positions and velocities of the
stations.
Then fixing the value of
and the principal nutation term are also difficult
to separate.
We have adopted the following strategy. First, we determine the whole set
of parameters mentioned above except the positions and velocities of the
stations.
Then fixing the value of 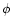 ,
we add the positions of the stations to the
whole set and make a new improvement. Next we determine the velocities
of the stations separately. Finally, fixing all the parameters, we perform
a last analysis including
,
we add the positions of the stations to the
whole set and make a new improvement. Next we determine the velocities
of the stations separately. Finally, fixing all the parameters, we perform
a last analysis including 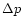 and the principal term of
and the principal term of
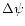 (nutation in longitude) (see Sect. 10).
At each step of the process we verify the coherence of the determinations;
for example we verify that the introduction of the fitted values of X, Y,
Z does not change significantly the value of
(nutation in longitude) (see Sect. 10).
At each step of the process we verify the coherence of the determinations;
for example we verify that the introduction of the fitted values of X, Y,
Z does not change significantly the value of 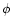 if the first step is
reiterated.
if the first step is
reiterated.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2201f2.eps}\end{figure}](/articles/aa/full/2002/20/aa2201/Timg30.gif) |
Figure 2:
Relative positions of the mean inertial ecliptic of J2000.0 with respect to
ICRS, MCEP and JPL. |


Up: A new determination of
Copyright ESO 2002
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{MS2201f2.eps}\end{figure}](/articles/aa/full/2002/20/aa2201/Timg30.gif)