10 The precession constant

The correction to the IAU76 constant of precession in (Chapront et al. 2000) was:

$$% \Delta_{1}p = -0.3164 \pm 0.0027 ''/{\rm cy}.$$ (1)

This value was presented at the IAU meeting in Manchester (Fukushima 2000a). It was obtained via the solution S2000, using Sol. 1 (MCEP), as mentioned above. With Sol. 1 (MCEP) of S2001, we get now:

$$\begin{eqnarray*}\Delta_{1}p = -0.3364 \pm 0.0027 ''/{\rm cy}. \end{eqnarray*}$$

The noticeable divergence of this new determination with respect to the previous one in (1) caught our attention and we noticed that in Sol. 2 (ICRS) a residual $\Delta_{2}p$ arises:

$$\begin{eqnarray*}\Delta_{2}p = -0.0316 \pm 0.0027 ''/{\rm cy}. \end{eqnarray*}$$

Sol. 1 (MCEP) and Sol. 2 (ICRS) use the same observations (the main source of errors) and the same models, except for the motion of the reference frame due to precession and nutation. Hence, the differences between the corrections $\Delta_{1}p$ and $\Delta_{2}p$ are mainly due to the precession-nutation models. If we assume that C04 $\delta\psi$ and $\delta\epsilon$ series used in Sol. 2 (ICRS) based on VLBI observations, contributes ideally to the precession-nutation matrix $P\times N$, the difference $\Delta_{1}p - \Delta_{2}p$ gives an estimate of the corrections that should be applied to the IAU76 precession constant. In particular this difference eliminates the effects of an improper motion of the stations, errors in the EOP series for Universal Time and polar motion, and a local bias produced by the observations themselves. Contrariwise all systematic effects or local errors in C04 $\delta\psi$ and $\delta\epsilon$ series are still in the difference.

 

 

Table 10: Correction to the IAU76 constant of precession $\Delta p$ (in arcsecond/cy) and offsets of Celestial Ephemeris Pole at J2000.0 $-\psi \sin\epsilon$ and $\Delta \epsilon$ (in arcsecond). The uncertainties are formal errors.

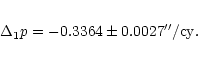
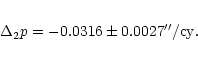
Method	Source	$\Delta p$	$-\psi \sin\epsilon$	$\Delta \epsilon$
VLBI	Fukushima (2000a)	-0.297  $\pm$  0.004	-0.0167 $\pm$ 0.0005	-0.0049 $\pm$ 0.0003
LLR	S1998	-0.344  $\pm$  0.004	-0.0183 $\pm$ 0.0004	-0.0056 $\pm$ 0.0002
LLR	S2000	-0.316  $\pm$  0.003	-0.0173 $\pm$ 0.0004	-0.0054 $\pm$ 0.0002
LLR	S2001 (this paper)	-0.302  $\pm$  0.003	-0.0177 $\pm$ 0.0004	-0.0054 $\pm$ 0.0002
	IAU 2000A (Mathews et al. 2002)	-0.29965

If we suppose that C04 $\delta\psi$ and $\delta\epsilon$ series do not contain any secular trends or bias, a more appropriate correction to the IAU76 constant of precession should then be done with:

$$\Delta p = \Delta_{1}p - \Delta_{2}p = -0.3048 ''/{\rm cy}.$$ (2)

Figure 4 illustrates the evolution of $\Delta_{1}p$ and $\Delta p = \Delta_{1}p - \Delta_{2}p$ when the upper limit of the time span covered by the fit varies. We see that, though $\Delta_{1}p$ varies, $\Delta p$ remains constant around the value -0.302''/cy, and we propose now this value as the LLR correction value.

Figure 4: Evolution of the correction to the IAU76 constant of precession with the upper limit of the time span covered by the fit.

The obliquity shows a similar phenomenon illustrated by Fig. 5. We note $\Delta_{1}\epsilon$ the correction obtained with Sol. 1 (MCEP) to a reference value of obliquity, $\Delta_{2}\epsilon$ the similar quantity obtained with Sol. 2 (ICRS), and $\Delta \epsilon$ the difference: $\Delta\epsilon = \Delta_{1}\epsilon - \Delta_{2}\epsilon$. A trend in $\Delta_{1}\epsilon$ is apparent in Fig. 5 (about $0.008\arcsec/$cy) but the difference $\Delta \epsilon$ is almost a constant. The trend in $\Delta_{1}\epsilon$ could make one believe in a correction to the obliquity rate -46''.8340/cy adopted in Sol. 1 (MCEP) from Williams (1994), but the similar trend in $\Delta_{2}\epsilon$ makes this hypothesis vanish. As for precession, the trends in $\Delta_{1}\epsilon$ and $\Delta_{2}\epsilon$ are rather due to an improper motion of the stations or to a local bias produced by the observations themselves. Note that trends are larger when positions and velocities of the stations are not improved (see Sect. 6).

Figure 5: Evolution of the correction to the obliquity with the upper limit of the time span covered by the fit.

In Table 10, we bring together our LLR determinations for the correction to the IAU76 constant of precession with the last values obtained by VLBI (Fukushima 2000b and Mathews et al. 2002), and the best estimates for the offsets of Celestial Ephemeris Pole at J2000.0, $-\psi \sin\epsilon(MCEP)$ and $\Delta \epsilon=\epsilon (MCEP)-\epsilon(ICRS)$. The last two quantities are denoted as $\theta_2$ and $-\theta_1$ in Chapront et al. (1999b), and $\Delta\psi \sin\epsilon_0$ and $\Delta \epsilon_0$ by Fukushima. We note that our values for $\Delta p$ are significantly different in S2001 and S1998. The nutation model and the weight distribution are deciding factors for the improvement of the solution. Now the value for $\Delta p$ obtained by LLR and VLBI converge nicely with a separation smaller than 0.03 mas/year.

We have also performed an analysis including the precession and the principal terms of nutations in longitude and obliquity. Although there is a strong correlation between precession and nutation, the final correction to the above $\Delta p$ is small ( +0.0082 ''/cy) and the amplitudes of the principal terms in nutations are not sensibly modified (0.5 mas for longitude and 0.02 mas for obliquity) within the formal errors.