The migration regime corresponding to the range of masses, aspect ratios and viscosities investigated in this work corresponds
mostly to type I migration regime, except the low aspect ratio, low viscosity and large mass runs, in which quite a significant gap
is opened in the co-orbital region. As type I migration is known to be too fast (i.e. the migration time of a protoplanetary core is
shorter than its build-up time), it is of interest to investigate the migration time from these results, as a function of aspect
ratio, planet mass and viscosity. Figures 25 and 26 show the migration time, in years, of a
protocore at 1 AU embedded respectively in a 3% and 4% aspect ratio disk. In either case the disk surface density is chosen to
be that of the minimum mass solar nebula (1700 g cm-2, i.e.
![]() ,
see Hayashi et al. 1985).
,
see Hayashi et al. 1985).
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{ref_fig25.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg256.gif) |
Figure 26: Migration time in years at 1 AU for a h=0.04 disk, as a function of planet mass and disk viscosity. The contour line style obeys the same conventions as in Fig. 25. |
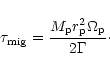 |
(41) |
It should also be noted that, as the corotation torque scales with the slope of the specific vorticity gradient, the torque reversal
that was found here for very thin disks is not likely to subsist if one takes a significant negative surface density gradient (i.e.
if
![]() with
with ![]() ).
).
On the other hand if the specific vorticity gradient is even steeper than the one envisaged here, then the corotation torque, depending on how steep this gradient is, may well unconditionally dominate the differential Lindblad torque. This might be the case in the very central parts of the disk, where the outer disk solution has to be connected to an inner cavity (e.g. magnetically cleared). If the transition region is larger than the co-orbital zone of an infalling body, then the corotation torque acting on it might be able to counteract the differential Lindblad torque, providing another way of stopping the inward migrating bodies, as the disk there is very likely to be viscous and therefore very likely to be able to sustain an unsaturated corotation torque.
As the analysis presented here is restricted to a planet held on a fixed circular orbit, it should be realized that the migration time-scale
estimated above is only valid whenever the viscous drift rate of material across the orbit is much larger than the planet inferred
drift rate
![]() ,
otherwise the corotation torque expression has to explicitly include a term
proportional to
,
otherwise the corotation torque expression has to explicitly include a term
proportional to ![]() ,
the migration rate, with a delay which scales as the outermost horseshoe libration
time. The domain for which the migration rate is negligible compared to the viscous drift radial velocity is shown in Figs. 25
and 26.
Therefore one can see that at very low viscosities [
,
the migration rate, with a delay which scales as the outermost horseshoe libration
time. The domain for which the migration rate is negligible compared to the viscous drift radial velocity is shown in Figs. 25
and 26.
Therefore one can see that at very low viscosities [
![]() -
-
![]() ]
the expression for the corotation
torque needs to be reconsidered, as most of the specific vorticity drift across the co-orbital region is not accounted for
by the viscous accretion but by the migration itself. In these circumstances the total torque felt by the planet depends
on its migration rate. The analyze and consequences of this feed-back will be presented elsewhere.
]
the expression for the corotation
torque needs to be reconsidered, as most of the specific vorticity drift across the co-orbital region is not accounted for
by the viscous accretion but by the migration itself. In these circumstances the total torque felt by the planet depends
on its migration rate. The analyze and consequences of this feed-back will be presented elsewhere.
Copyright ESO 2002