

Up: The co-orbital corotation torque
Subsections
5 Smoothing issues and 3D expectations
The above simulations are performed in 2D, and the disk finite thickness is taken into
account through the use of a smoothing coefficient 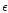 in the potential, where
in the potential, where
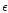 is a sizable fraction of the disk vertical scale length
is a sizable fraction of the disk vertical scale length
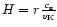 .
One can wonder how accurate this description is, and what fraction
.
One can wonder how accurate this description is, and what fraction
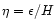 of the disk
thickness should be used in order to get as close as possible a result to the
3D expectations. Moreover, there is no reason that an adequate value of
of the disk
thickness should be used in order to get as close as possible a result to the
3D expectations. Moreover, there is no reason that an adequate value of 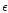 for the
Lindblad torque (in the sense that this value of
for the
Lindblad torque (in the sense that this value of 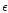 will provide a value for the
one-sided and/or differential Lindblad torque in agreement with results obtained with
three dimensional calculations, see e.g. Miyoshi et al. 1999) will also be an adequate value
for the corotation torque.
The following discussion is therefore divided in two parts:
the effect of smoothing on the Lindblad torque is first investigated, then secondly on the corotation torque, and lastly it is discussed
whether Lindblad and corotation torques can be described appropriately by the
same smoothing coefficient.
will provide a value for the
one-sided and/or differential Lindblad torque in agreement with results obtained with
three dimensional calculations, see e.g. Miyoshi et al. 1999) will also be an adequate value
for the corotation torque.
The following discussion is therefore divided in two parts:
the effect of smoothing on the Lindblad torque is first investigated, then secondly on the corotation torque, and lastly it is discussed
whether Lindblad and corotation torques can be described appropriately by the
same smoothing coefficient.
Figure 18 shows the ratio of the one-sided Lindblad torque for
a smoothed potential and the one-sided Lindblad torque for an unsmoothed potential, as a
function of the ratio of the smoothing length to the disk thickness. The one-sided Lindblad torque is
evaluated by the arithmetical average of the outer and inner Lindblad
torque expressions, which are:
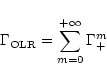 |
(26) |
and:
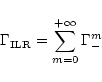 |
(27) |
where:
![\begin{displaymath}
\Gamma_\varepsilon^m=-\varepsilon\pi m\frac{[\psi_m^\varepsilon(h,\epsilon)]^2h^
3}{(rdD/dr)_{r_m^\varepsilon}}
\end{displaymath}](/articles/aa/full/2002/20/aa1942/img195.gif) |
(28) |
in which
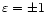 (for Outer/Inner Lindblad resonance respectively), and
where:
(for Outer/Inner Lindblad resonance respectively), and
where:
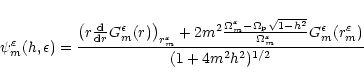 |
(29) |
in which
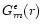 is a generalized Laplace coefficient (i.e. a Laplace coefficient for which a smoothing
is introduced):
is a generalized Laplace coefficient (i.e. a Laplace coefficient for which a smoothing
is introduced):
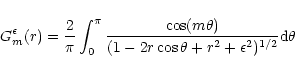 |
(30) |
and where:
![\begin{displaymath}
\Omega_m^\varepsilon=\Omega_{\rm p}[(1-h^2)^{1/2}+\varepsilon m^{-1}(1+m^2h^2)^{1/2}]^{-1}
\end{displaymath}](/articles/aa/full/2002/20/aa1942/img200.gif) |
(31) |
is the Keplerian frequency at the effective location of the Lindblad resonances,
and:
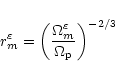 |
(32) |
and we use:
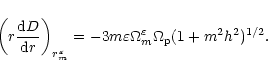 |
(33) |
This calculation is identical to the calculation in Ward (1997) except for the introduction
of the smoothing of the perturbing potential.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{aa1942f13.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg203.gif) |
Figure 18:
One-sided Lindblad torque cut-off as a function of the relative smoothing
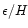 .
The long dashed line represents the approximate asymptotic solution for .
The long dashed line represents the approximate asymptotic solution for
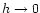 deduced from Eq. (34).
deduced from Eq. (34). |
The cut-off function is shown for three different aspect ratios, and found to be only weakly dependent
on h. At low aspect ratio, the functional dependence of the torque cut-off tends towards
a fixed function, the graph of which should roughly coincide with the solid curve of
Fig. 18. An approximation of the limit cut-off function when
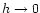 can be
obtained by developing Eq. (30)
to first order in mh, and
approximating the
can be
obtained by developing Eq. (30)
to first order in mh, and
approximating the
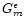 coefficients
with a standard technique as a function of the Bessel K0 and K1 functions. The
summation over m can then be approximated as an integral. Using the variables
coefficients
with a standard technique as a function of the Bessel K0 and K1 functions. The
summation over m can then be approximated as an integral. Using the variables 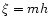 and
and
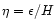 ,
one can finally write the following approximate formula for the one-sided Lindblad
torque as a function of the relative smoothing
,
one can finally write the following approximate formula for the one-sided Lindblad
torque as a function of the relative smoothing 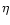 only:
only:
![\begin{displaymath}
\gamma_{\rm LR}(\eta)=K\int_0^\infty\xi^2\frac{(1+\xi^2)^{1/...
...4\xi^2}
F\left[\frac 49(1+\xi^2)+\xi^2\eta^2\right]{\rm d}\xi~
\end{displaymath}](/articles/aa/full/2002/20/aa1942/img206.gif) |
(34) |
where K is a constant and:
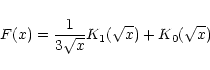 |
(35) |
where K0and K1 are the modified Bessel functions. The long dashed line of Fig. 18 is
the graph of the cut-off
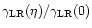 .
Figure 19 shows the behavior of the differential Lindblad torque cut-off for the same set of disk thicknesses.
This cut-off exhibits quite similar a behavior to the one-sided Lindblad torque cut-off.
.
Figure 19 shows the behavior of the differential Lindblad torque cut-off for the same set of disk thicknesses.
This cut-off exhibits quite similar a behavior to the one-sided Lindblad torque cut-off.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{aa1942f14.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg209.gif) |
Figure 19:
Differential Lindblad torque cut-off as a function of the relative smoothing
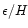 . . |
In Figs. 18 and 19 the dot-dashed line shows the value of the
smoothing for which the torque cut-off amounts to 0.43, which is the value quoted by Miyoshi et al. (1999)
for the ratio of the Lindblad torque in a vertically resolved disk and in an infinitesimally thin disk, in the linear regime. The corresponding relative smoothing is 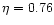 ,
both on the one-sided Lindblad
torque and on the differential Lindblad torque. Therefore a potential smoothing length of 76% of the disk thickness should be used in 2D simulations in order to give correct results for the (differential) Lindblad
torque. The fact that this value is independent of the disk aspect ratio and planet mass (at least in the linear regime) comes from the fact that most of the torque between the disk and the planet comes from a
zone which is at a distance
,
both on the one-sided Lindblad
torque and on the differential Lindblad torque. Therefore a potential smoothing length of 76% of the disk thickness should be used in 2D simulations in order to give correct results for the (differential) Lindblad
torque. The fact that this value is independent of the disk aspect ratio and planet mass (at least in the linear regime) comes from the fact that most of the torque between the disk and the planet comes from a
zone which is at a distance 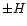 from the orbit (the Lindblad resonances pile up for
from the orbit (the Lindblad resonances pile up for
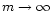 at a distance
at a distance
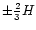 from the orbit). Such an argument cannot be used for the co-orbital corotation
torque which needs a different treatment.
from the orbit). Such an argument cannot be used for the co-orbital corotation
torque which needs a different treatment.
The corotation torque comes from the exchange of angular momentum between the planet and nearby,
orbit crossing fluid elements (which can be either fluid elements librating on closed, horseshoe like
streamlines, or fluid elements participating in the global viscous accretion of the disk, and which
pass by the planet as they go from the outer disk to the inner disk). As a fluid element participating
in the corotation torque,
with impact parameter
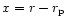 ,
will be located at a distance -x from the orbit after a back-scattering
by the planet, the specific angular momentum that it gives to the planet is
,
will be located at a distance -x from the orbit after a back-scattering
by the planet, the specific angular momentum that it gives to the planet is
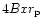 ,
and therefore this value
does not depend on smoothing. The total value of the corotation torque does depend on it however,
since the radial width of the libration region depends on the smoothing: the smaller the smoothing,
the further the separatrices lie from the orbit, and the larger the corotation torque.
,
and therefore this value
does not depend on smoothing. The total value of the corotation torque does depend on it however,
since the radial width of the libration region depends on the smoothing: the smaller the smoothing,
the further the separatrices lie from the orbit, and the larger the corotation torque.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{sfig15.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg217.gif) |
Figure 20:
Total torque acting on the planet, as a function of the reduced viscosity,
for runs
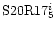 , ,
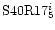 and R175i.
and R175i. |
This behavior can be checked at Fig. 20. The runs for a planet of mass
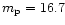
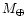 have been performed with three different smoothing values. At low viscosity (i.e.
for a saturated corotation torque) the total torque is negative and has a larger absolute value for a smaller
smoothing. This corresponds to expectations since the torque in this region (whether it
includes the Lindblad torque coupling term of the corotation torque or not) scales as the
(one-sided or differential) Lindblad torque. On the other hand, the difference between the maximum value of the
torque with the minimum value at low viscosity should roughly correspond to the maximum value
of the
corotation torque main term, which scales as
have been performed with three different smoothing values. At low viscosity (i.e.
for a saturated corotation torque) the total torque is negative and has a larger absolute value for a smaller
smoothing. This corresponds to expectations since the torque in this region (whether it
includes the Lindblad torque coupling term of the corotation torque or not) scales as the
(one-sided or differential) Lindblad torque. On the other hand, the difference between the maximum value of the
torque with the minimum value at low viscosity should roughly correspond to the maximum value
of the
corotation torque main term, which scales as
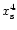 .
At Fig. 21 we plot this difference as a function of
the separatrix distance to the orbit
.
At Fig. 21 we plot this difference as a function of
the separatrix distance to the orbit 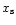 .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{aa1942f16.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg221.gif) |
Figure 21:
Corotation torque main term estimate as a function of the separatrix position. The dotted line correspond
to a fourth power of 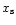 ,
and the dashed one to a third power of ,
and the dashed one to a third power of 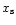 . . |
Despite the small number of measurements, the results are in good agreement with a
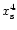 dependency
of the corotation torque. This also confirms the argument exposed above
that the corotation torque depends on the smoothing only through
the value of
dependency
of the corotation torque. This also confirms the argument exposed above
that the corotation torque depends on the smoothing only through
the value of 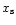 .
.
It is worth emphasizing the dramatic dependence of the corotation torque on smoothing.
In Fig. 20, for a smoothing length that is 60% of the disk thickness,
the torque is always negative, although it can reach a value one order of magnitude smaller than the
differential Lindblad torque linear estimate for an unsmoothed potential. On the other hand, a smoothing
length that is 20% of the disk thickness leads to a torque reversal over a significant range
of viscosity (
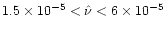 ,
which corresponds to
,
which corresponds to
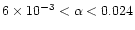 ).
).
An idea of the co-orbital dynamics in a three dimensional situation can be obtained simply if one assumes
that the motion is purely horizontal. In that case the motion in the slice of altitude z and infinitely
small thickness dz is equivalent to a 2D situation, in which the potential smoothing length is z. Furthermore,
as for
 the specific angular momentum radial gradient is still
the specific angular momentum radial gradient is still
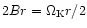 ,
the torque contribution
of the slice is the same as the torque exerted by an infinitesimally thin disk (with a potential smoothed over
a length z) of surface density
,
the torque contribution
of the slice is the same as the torque exerted by an infinitesimally thin disk (with a potential smoothed over
a length z) of surface density
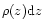 .
Let
.
Let
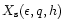 be the separatrix distance to the orbit
in an infinitesimally thin disk in the equatorial plane, in which the potential is smoothed over a length
be the separatrix distance to the orbit
in an infinitesimally thin disk in the equatorial plane, in which the potential is smoothed over a length 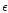 ,
the sound speed
is
,
the sound speed
is
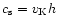 ,
and the planet to primary mass ratio is q. The fully unsaturated corotation torque main term
in a thick disk can therefore be written as:
,
and the planet to primary mass ratio is q. The fully unsaturated corotation torque main term
in a thick disk can therefore be written as:
![\begin{displaymath}
\Gamma_{\rm c}=\int_{-\infty}^{+\infty}\frac 98\Omega_{\rm p...
...m s}^4\left[z,q,\frac{c_{\rm s}(z)}{v_{\rm K}}\right]{\rm d}z.
\end{displaymath}](/articles/aa/full/2002/20/aa1942/img229.gif) |
(36) |
As this analysis is restricted to the case of isothermal Keplerian disks, Eq. (36) can be recast as:
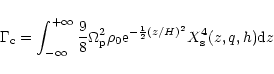 |
(37) |
where 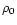 is the disk density in the equatorial plane. Eq. (36) can also be written as:
is the disk density in the equatorial plane. Eq. (36) can also be written as:
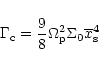 |
(38) |
in which
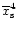 is defined as:
is defined as:
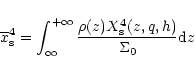 |
(39) |
which can be recast as:
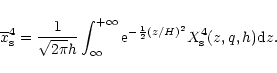 |
(40) |
Therefore, if one wants a 2D simulation to give the correct amplitude for the fully unsaturated corotation
torque main term, one needs to use the smoothing length which endows the co-orbital motion with a separatrix
position
 ,
where
,
where
 is given by Eq. (40). The integrand of the
right hand side contains the function
is given by Eq. (40). The integrand of the
right hand side contains the function 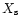 ,
which has to be tabulated a priori with a set of runs with different
smoothing lengths, for a given planet mass and disk aspect ratio. The same tabulation is used to infer
the correct value for
,
which has to be tabulated a priori with a set of runs with different
smoothing lengths, for a given planet mass and disk aspect ratio. The same tabulation is used to infer
the correct value for 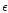 once
once
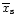 is known.
is known.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{aa1942f17.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg238.gif) |
Figure 22:
Separatrix distance to the orbit as a function of the relative smoothing
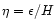 ,
for different aspect ratios and planet masses
( ,
for different aspect ratios and planet masses
(
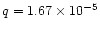 :
dashed lines, :
dashed lines,
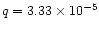 :
dotted lines, and :
dotted lines, and
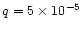 :
solid lines). As expected, :
solid lines). As expected, 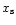 decreases as the smoothing increases, decreases as the aspect ratio increases (everything else being fixed), and increases as the mass increases (everything else being fixed).
decreases as the smoothing increases, decreases as the aspect ratio increases (everything else being fixed), and increases as the mass increases (everything else being fixed). |
Figure 22 shows such tabulations for different planet masses and disk aspect ratios. They are
measured with a dichotomic search of the separatrix position on the results of low viscosity runs (
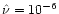 ), over 150 orbits.
), over 150 orbits.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa1942f24.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg240.gif) |
Figure 23:
Corotation torque adapted smoothing as a function of
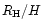 ,
inferred from the tabulations of Fig. 22. ,
inferred from the tabulations of Fig. 22. |
Figure 23 shows the results of this integration for the nine situations of Fig. 22. It can be seen that on the contrary to
the case of the Lindblad torque, the value of the correct smoothing depends on
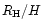 even when this value is below 1/2. Furthermore,
in this case, which corresponds to the linear regime for the Lindblad torque, the correct smoothing length is clearly smaller (50-60% of the
disk thickness) than the correct smoothing length for the Lindblad torque (76% of the disk thickness). The choice of any value between
60 and 76% of the disk thickness will therefore underestimate the corotation torque and overestimate the Lindblad torque,
and therefore in any case will underestimate the total torque, since the differential Lindblad torque is negative
and the corotation torque is positive.
Furthermore, as the corotation torque is a very sensitive function of the smoothing, there is little hope of finding
a correct smoothing prescription which predicts a correct total torque value in a 2D simulation, especially in the cases of interest where the
corotation torque and differential Lindblad torque almost cancel out. One can however make conservative assumptions to infer the direction
of migration of a protoplanet by choosing a lower or upper limit for the smoothing coefficient. This is the object of the next section which
presents four series of selected high resolution runs.
even when this value is below 1/2. Furthermore,
in this case, which corresponds to the linear regime for the Lindblad torque, the correct smoothing length is clearly smaller (50-60% of the
disk thickness) than the correct smoothing length for the Lindblad torque (76% of the disk thickness). The choice of any value between
60 and 76% of the disk thickness will therefore underestimate the corotation torque and overestimate the Lindblad torque,
and therefore in any case will underestimate the total torque, since the differential Lindblad torque is negative
and the corotation torque is positive.
Furthermore, as the corotation torque is a very sensitive function of the smoothing, there is little hope of finding
a correct smoothing prescription which predicts a correct total torque value in a 2D simulation, especially in the cases of interest where the
corotation torque and differential Lindblad torque almost cancel out. One can however make conservative assumptions to infer the direction
of migration of a protoplanet by choosing a lower or upper limit for the smoothing coefficient. This is the object of the next section which
presents four series of selected high resolution runs.


Up: The co-orbital corotation torque
Copyright ESO 2002
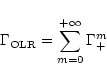
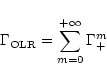
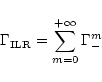
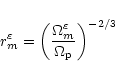
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{aa1942f13.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg203.gif)
![]() can be
obtained by developing Eq. (30)
to first order in mh, and
approximating the
can be
obtained by developing Eq. (30)
to first order in mh, and
approximating the
![]() coefficients
with a standard technique as a function of the Bessel K0 and K1 functions. The
summation over m can then be approximated as an integral. Using the variables
coefficients
with a standard technique as a function of the Bessel K0 and K1 functions. The
summation over m can then be approximated as an integral. Using the variables ![]() and
and
![]() ,
one can finally write the following approximate formula for the one-sided Lindblad
torque as a function of the relative smoothing
,
one can finally write the following approximate formula for the one-sided Lindblad
torque as a function of the relative smoothing ![]() only:
only:
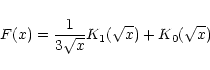
![]() ,
will be located at a distance -x from the orbit after a back-scattering
by the planet, the specific angular momentum that it gives to the planet is
,
will be located at a distance -x from the orbit after a back-scattering
by the planet, the specific angular momentum that it gives to the planet is
![]() ,
and therefore this value
does not depend on smoothing. The total value of the corotation torque does depend on it however,
since the radial width of the libration region depends on the smoothing: the smaller the smoothing,
the further the separatrices lie from the orbit, and the larger the corotation torque.
,
and therefore this value
does not depend on smoothing. The total value of the corotation torque does depend on it however,
since the radial width of the libration region depends on the smoothing: the smaller the smoothing,
the further the separatrices lie from the orbit, and the larger the corotation torque.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{sfig15.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg217.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{aa1942f16.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg221.gif)
![]() ,
which corresponds to
,
which corresponds to
![]() ).
).
![]() the specific angular momentum radial gradient is still
the specific angular momentum radial gradient is still
![]() ,
the torque contribution
of the slice is the same as the torque exerted by an infinitesimally thin disk (with a potential smoothed over
a length z) of surface density
,
the torque contribution
of the slice is the same as the torque exerted by an infinitesimally thin disk (with a potential smoothed over
a length z) of surface density
![]() .
Let
.
Let
![]() be the separatrix distance to the orbit
in an infinitesimally thin disk in the equatorial plane, in which the potential is smoothed over a length
be the separatrix distance to the orbit
in an infinitesimally thin disk in the equatorial plane, in which the potential is smoothed over a length ![]() ,
the sound speed
is
,
the sound speed
is
![]() ,
and the planet to primary mass ratio is q. The fully unsaturated corotation torque main term
in a thick disk can therefore be written as:
,
and the planet to primary mass ratio is q. The fully unsaturated corotation torque main term
in a thick disk can therefore be written as:
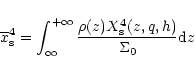
![\begin{figure}
\par\includegraphics[width=8cm,clip]{aa1942f24.ps}
\end{figure}](/articles/aa/full/2002/20/aa1942/Timg240.gif)