The code that was used is an Eulerian ZEUS-like 2D code based on a polar
grid centered on the primary (Stone & Norman 1992; Nelson et al. 2000),
and corotating with the planet (Kley 1998).
The runs described here were performed using a modified azimuthal
Courant condition (Masset 2000) in order to increase the timestep, and some
of these runs were checked against the standard azimuthal transport procedure,
and found to give almost identical results. The grid consists of
![]() by Nr=143 zones, uniformly spaced in azimuth and radius.
The planet lies at radius
by Nr=143 zones, uniformly spaced in azimuth and radius.
The planet lies at radius
![]() and azimuth
and azimuth ![]() .
The central star mass
and gravitational constant are respectively M*=1 and G=1, and the
time unit is chosen to be
.
The central star mass
and gravitational constant are respectively M*=1 and G=1, and the
time unit is chosen to be
![]() ,
so that
the planet orbital period in our unit system is
,
so that
the planet orbital period in our unit system is ![]() .
The grid outer boundary
is chosen to be at r=2.5, while the inner boundary is at
r=0.504651,
so that the planet is located just at the center of a zone, in order to
limit any bias in the torque and in the co-orbital dynamics due to an uneven
placement of the planet w.r.t. the grid.
.
The grid outer boundary
is chosen to be at r=2.5, while the inner boundary is at
r=0.504651,
so that the planet is located just at the center of a zone, in order to
limit any bias in the torque and in the co-orbital dynamics due to an uneven
placement of the planet w.r.t. the grid.
The equations solved by the code are:
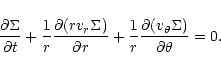 |
(4) |
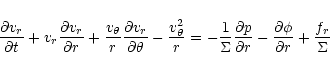 |
(5) |
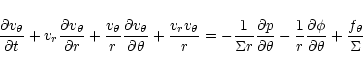 |
(6) |
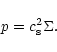 |
(7) |
The boundary conditions are ![]() -periodic in
-periodic in ![]() in order
to account for the disk geometry.
As the viscosity can be large in some runs, it is important to take adequate
boundary conditions, otherwise the fast radial redistribution of disk material
can affect the slope of the surface density profile, which in turn can significantly
alter the corotation torque magnitude. For this reason, it is important :
in order
to account for the disk geometry.
As the viscosity can be large in some runs, it is important to take adequate
boundary conditions, otherwise the fast radial redistribution of disk material
can affect the slope of the surface density profile, which in turn can significantly
alter the corotation torque magnitude. For this reason, it is important :
In all the runs presented here, the unperturbed disk surface density is
uniform and is, in our unit system,
![]() .
This translates
into:
.
This translates
into:
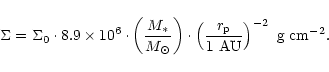 |
(13) |
The disk temperature profile is constant in time and is chosen such that
the disk aspect ratio h=H/r be uniform. The initial azimuthal velocity
is computed
accordingly and is slightly sub-Keplerian due to the partial support of
gravity by the radial pressure gradient:
![\begin{displaymath}v_\theta=\left[\frac{GM_*}{r}(1-h^2)\right]^{1/2}.
\end{displaymath}](/articles/aa/full/2002/20/aa1942/img105.gif) |
(14) |
A number of runs have been performed varying the planet mass, the disk aspect
ratio, the viscosity, and in some cases the smoothing prescription or
the resolution (which was then chosen twice higher). Each run consisted of
120 planet orbits (which was assumed to be sufficient to reach
a steady state in the planet frame). For a given choice of the planet
mass and disk aspect ratio, usually 13 runs were performed for different
values of the viscosity, logarithmicly spaced:
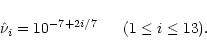 |
(15) |
|
|
3 | 4 | 5 | 6 |
|
|
|
|
|
n/a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 10-4 | n/a |
|
|
|
Subsidiary runs have been performed in which either the smoothing or the resolution has been changed with respect to the main runs. These runs are presented at Table 2.
| Run name | corresponding main run | parameter changed |
| S20R155i | R155i,
|
Smoothing:
|
| S40R155i | R155i,
|
Smoothing:
|
Subsidiary runs have been performed in which either the smoothing or the resolution has been changed with respect to the main runs. The runs with a modified smoothing length are presented at Table 2, whereas the high resolution runs are presented at Sect. 6.
Copyright ESO 2002