

Up: Photometric redshifts from evolutionary
Subsections
4 Sensitivity to parameters
Table 2 summarizes the comparison
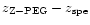 and the corresponding dispersion, given by a series of various Z-PEG models
computed by changing only one parameter. The considered parameters are age, absorption
by the IGM and the addition of NIR colors (JHK).
We evaluate the offset and the dispersion of the
and the corresponding dispersion, given by a series of various Z-PEG models
computed by changing only one parameter. The considered parameters are age, absorption
by the IGM and the addition of NIR colors (JHK).
We evaluate the offset and the dispersion of the
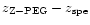 distribution with
distribution with
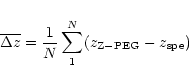 |
(2) |
![\begin{displaymath}\sigma^2_z=\frac{1}{N-1} \sum _1^N \left[ (z_{{\rm Z-PEG}}-z_{{\rm spe}})-\overline{\Delta z}~\right]^2
\end{displaymath}](/articles/aa/full/2002/17/aa2109/img84.gif) |
(3) |
where N is the number of solutions. Most teams only limit their
results and corresponding error bars to primary solutions for
 .
In such cases, N is the number of galaxies in the sample.
Yet, as the uncertainties on
.
In such cases, N is the number of galaxies in the sample.
Yet, as the uncertainties on
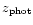 are often underestimated (see Sect. 2.2),
we choose to use
are often underestimated (see Sect. 2.2),
we choose to use
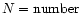 of primary solutions + number of secondary solutions.
Thus, the estimation of the dispersion is made with more points than the number of galaxies.
As a consequence, the value of the dispersion differs from the dispersion computed using
only primary solutions: the latter value might, by chance, be sometimes smaller.
This is the case when the number of galaxies for which the primary solution
is in agreement with the real redshift, dominates.
of primary solutions + number of secondary solutions.
Thus, the estimation of the dispersion is made with more points than the number of galaxies.
As a consequence, the value of the dispersion differs from the dispersion computed using
only primary solutions: the latter value might, by chance, be sometimes smaller.
This is the case when the number of galaxies for which the primary solution
is in agreement with the real redshift, dominates.
The basic procedure of the spectral synthesis of distant galaxies
requires one to respect the observed SEDs of standard nearby galaxies.
The correction factors (k-correction for expansion and e-correction for
evolution) are computed from the z=0 templates, fitting at best
observational data.
As a consequence, a z=0 age of the
stellar population is imposed by the synthetic SED template.
When the so-called z=0 age constraint is
taken into account, the dispersion
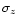 is reduced by 15% for z<1.5 (
is reduced by 15% for z<1.5 (
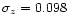 with model Z-PEG.1, Fig. 2,
compared to
with model Z-PEG.1, Fig. 2,
compared to
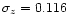 with model Z-PEG.2, Fig. 5).
For 0<z<5, the improvement factor is 8%.
As discussed above, computations with evolution require the age
constraint in order to make synthetic redshifted templates compatible
with z=0 observed templates. As discussed below, a similar constraint is used
in the interpretation models of faint galaxy counts
(see Fioc & Rocca-Volmerange 1999a). The remark is all the more important as
most photometric redshift models, even with evolution corrections, compute redshifts
without the age constraint, finding fits with synthetic templates
sometimes unable to reproduce z=0 galaxies.
Yet, we demonstrate here that our strong age constraint and the use of
appropriate scenarios of evolution give better results than the often-used
"no age constraint'' method.
with model Z-PEG.2, Fig. 5).
For 0<z<5, the improvement factor is 8%.
As discussed above, computations with evolution require the age
constraint in order to make synthetic redshifted templates compatible
with z=0 observed templates. As discussed below, a similar constraint is used
in the interpretation models of faint galaxy counts
(see Fioc & Rocca-Volmerange 1999a). The remark is all the more important as
most photometric redshift models, even with evolution corrections, compute redshifts
without the age constraint, finding fits with synthetic templates
sometimes unable to reproduce z=0 galaxies.
Yet, we demonstrate here that our strong age constraint and the use of
appropriate scenarios of evolution give better results than the often-used
"no age constraint'' method.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f6.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg88.gif) |
Figure 5:
Photometric redshift estimations like in Fig. 2
when our computations are free of any age constraint (model Z-PEG.2).
The dotted diagonal line is the linear regression of points
with
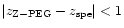 .
The dashed line
is the linear regression without the IGM absorption (model Z-PEG.3). .
The dashed line
is the linear regression without the IGM absorption (model Z-PEG.3). |
Moreover, not constraining the z=0 ages of galaxies (models Z-PEG.2 and beyond)
increases the age-redshift-type degeneracy (see Fig. 6,
left hand side): at a given redshift, a young (<1 Gyr) elliptical
galaxy would be an acceptable
solution, with almost the same optical colors as an old irregular one.
But using the model Z-PEG.1
that takes care of ages, we restrain the acceptable range
in the age-redshift-type space and raise partially a degeneracy.
Figure 6 clearly shows this effect on galaxy number 319 of
the FSLY sample.
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{MS2109f7.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg89.gif) |
Figure 6:
Fit of galaxy 319 (number from FSLY).
On the left hand side, the fit is made with model Z-PEG.2
(without age constraint) and on the right hand side we use model Z-PEG.1
(with age constraint): a) observed colors with ten times magnified error bars (for plotting only) and best-fitting synthetic SED,
b)  map on the age-z plane (black corresponds to low
map on the age-z plane (black corresponds to low  ),
c) ),
c)  projection on the age axis, d)
projection on the age axis, d)  projection on the redshift axis,
and e) Type maps on the age-z plane; the age-z solutions found in b) are also plotted.
The model Z-PEG.2 (left) shows several minimum redshifts around 1 whereas model
Z-PEG.1 (right) only shows one minimum close to the spectroscopic redshift
(
zspe=0.961).
projection on the redshift axis,
and e) Type maps on the age-z plane; the age-z solutions found in b) are also plotted.
The model Z-PEG.2 (left) shows several minimum redshifts around 1 whereas model
Z-PEG.1 (right) only shows one minimum close to the spectroscopic redshift
(
zspe=0.961). |
Since the strong discontinuities (4000 Å, Lyman break) are the most
constraining features for redshift determinations, several consequences
are implied (see also discussions in Bolzonella et al. 2000 and Massarotti et al. 2001a).
The observations of colors in the near infrared is the only way to follow
the discontinuities at the highest redshifts (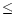 4.5 for the 4000 Å discontinuity
and
4.5 for the 4000 Å discontinuity
and 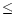 23 for the Lyman break in the K band). Moreover SED continua also contribute
to the best fits, so that in most cases, minimizing the
23 for the Lyman break in the K band). Moreover SED continua also contribute
to the best fits, so that in most cases, minimizing the  on the largest
wavelength coverage will decrease the degeneracy. Figure 7
and Table 2 show that without J, H and K bands, the photometric
redshift determination is poor (
on the largest
wavelength coverage will decrease the degeneracy. Figure 7
and Table 2 show that without J, H and K bands, the photometric
redshift determination is poor (
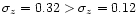 for
for
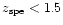 ).
Moreover, we do not use any filter between 8500 and
).
Moreover, we do not use any filter between 8500 and 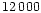 Å to fit the data,
because on the one hand we do not have the corresponding observations and on the other hand
only very few galaxies in our sample are at 1<z<2.
To analyze galaxies in the redshift range 1<z<2 , a Z filter
(or equivalent) would be necessary for observations as well as modeling.
Å to fit the data,
because on the one hand we do not have the corresponding observations and on the other hand
only very few galaxies in our sample are at 1<z<2.
To analyze galaxies in the redshift range 1<z<2 , a Z filter
(or equivalent) would be necessary for observations as well as modeling.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f8.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg93.gif) |
Figure 7:
Comparison of the photometric redshifts from Z-PEG (model Z-PEG.4) with the HDF-N measured spectroscopic redshifts without J, H, K bands, and without any particular age constraint. These results have to be compared to Fig. 5 for which there is no age constraint either. The dotted line is the linear regression of our photometric redshifts
if we exclude the points with
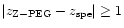 . . |
When comparing results with and without IGM absorption (Fig. 5),
an important deviation to the spectroscopic redshifts is observed
at high redshifts if we do not take the IGM into account: a linear regression
on fits without the IGM shows a systematic deviation towards high photometric redshifts. This was already noted by
Massarotti et al. (2001a, 2001b), and can be understood quite easily:
not including IGM absorption in models, one can mistake the Lyman forest
absorption by intergalactic Hi (below
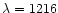 Å) for
the real Lyman break (
Å) for
the real Lyman break (
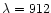 Å in the rest frame).
In such a case, we overestimate the redshift.
Å in the rest frame).
In such a case, we overestimate the redshift.


Up: Photometric redshifts from evolutionary
Copyright ESO 2002
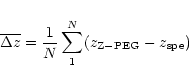
![\begin{displaymath}\sigma^2_z=\frac{1}{N-1} \sum _1^N \left[ (z_{{\rm Z-PEG}}-z_{{\rm spe}})-\overline{\Delta z}~\right]^2
\end{displaymath}](/articles/aa/full/2002/17/aa2109/img84.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f6.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=15.7cm,clip]{MS2109f7.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg89.gif)
![]() 4.5 for the 4000 Å discontinuity
and
4.5 for the 4000 Å discontinuity
and ![]() 23 for the Lyman break in the K band). Moreover SED continua also contribute
to the best fits, so that in most cases, minimizing the
23 for the Lyman break in the K band). Moreover SED continua also contribute
to the best fits, so that in most cases, minimizing the ![]() on the largest
wavelength coverage will decrease the degeneracy. Figure 7
and Table 2 show that without J, H and K bands, the photometric
redshift determination is poor (
on the largest
wavelength coverage will decrease the degeneracy. Figure 7
and Table 2 show that without J, H and K bands, the photometric
redshift determination is poor (
![]() for
for
![]() ).
Moreover, we do not use any filter between 8500 and
).
Moreover, we do not use any filter between 8500 and ![]() Å to fit the data,
because on the one hand we do not have the corresponding observations and on the other hand
only very few galaxies in our sample are at 1<z<2.
To analyze galaxies in the redshift range 1<z<2 , a Z filter
(or equivalent) would be necessary for observations as well as modeling.
Å to fit the data,
because on the one hand we do not have the corresponding observations and on the other hand
only very few galaxies in our sample are at 1<z<2.
To analyze galaxies in the redshift range 1<z<2 , a Z filter
(or equivalent) would be necessary for observations as well as modeling.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS2109f8.eps}\end{figure}](/articles/aa/full/2002/17/aa2109/Timg93.gif)