The flux
![]() (ergs cm-2 s-1), of an optically thin
spectral line of wavelength
(ergs cm-2 s-1), of an optically thin
spectral line of wavelength
![]() is
is
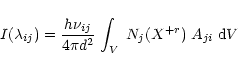 |
(1) |
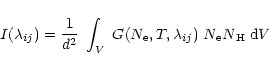 |
(2) |
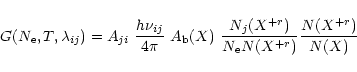 |
(3) |
Note that the determination of the DEM(T) distribution is an ill-posed problem (see, e.g. Craig & Brown 1986; McIntosh 2000, and references therein) where solutions are not unique. However, improvements can be made with a careful selection of lines, and the larger uncertainties become those associated with either the observational data or the atomic physics calculations. Also note that the DEM(T) does not necessarily have a direct physical significance (in terms of e.g. a temperature gradient), unless other factors are taken into account. For example, filling factors (cf. Judge 2000) are known to be small in the transition region, and probably different from those of the low corona.
Once the DEM is derived from a set of observed fluxes,
it is possible to calculate
an emission measure value
![]() for each
temperature Ti, once a temperature
interval
for each
temperature Ti, once a temperature
interval ![]() is defined:
is defined:
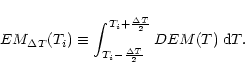 |
(5) |
Another definition that is commonly used
(see, e.g. Griffiths & Jordan 1998, and references therein)
involves differentiation over the logarithm of the temperature:
![]() .
This definition is more convenient when an approximation for the
volume emission measure is sought. In fact, if one defines
an average temperature T0 such as
log
.
This definition is more convenient when an approximation for the
volume emission measure is sought. In fact, if one defines
an average temperature T0 such as
log
![]() ,
and assumes that
,
and assumes that
![]() varies linearly with
varies linearly with ![]() ,
the total emission measure over an interval
,
the total emission measure over an interval
![]() centred at T0 can be approximated with what is generally termed the
EM(0.3) value (cf. Griffiths & Jordan 1998):
centred at T0 can be approximated with what is generally termed the
EM(0.3) value (cf. Griffiths & Jordan 1998):
 |
(6) |
Another different and common approach (see Fig. 8) is to plot the
ratio
![]() for each line
as a function of temperature and consider the loci of these curves
to constrain the shape of the emission measure distribution.
In fact, for each line and temperature Ti the value
for each line
as a function of temperature and consider the loci of these curves
to constrain the shape of the emission measure distribution.
In fact, for each line and temperature Ti the value
![]() represents an upper limit to the value of the
emission measure at that temperature
(assuming that all the observed emission
represents an upper limit to the value of the
emission measure at that temperature
(assuming that all the observed emission
![]() is produced by plasma at temperature Ti).
is produced by plasma at temperature Ti).
It should be noted that the ionisation equilibrium plays a major role not only in the derivation of the DEM, but also in that one of the elemental abundances.
The anomalous behaviour of the ions of the Li and Na isoelectronic sequences has been known for more than 30 years. For anomalous behaviour we mean that once a DEM analysis is performed using lines from different isoelectronic sequences, the theoretical intensities of the lines of the anomalous ions are consistently under- or over-estimated by large factors. Burton et al. (1971) reported this anomalous behaviour based on a solar spectrum from a rocket flight. Dupree (1972) confirmed this anomaly, using OSO-IV solar spectra. A possible explanation of this anomaly resides in the density dependence of the ionisation fractions. Burgess & Summers (1969) showed that the density dependence of the dielectronic recombination, together with the collisional ionisations from metastable levels produce significant changes in the ionisation fractions. Vernazza & Raymond (1978) took into account these effects and showed that significant increases in the line intensities of the Li-like ions occur at high densities. The same applies to the Na-like ions, and, to a lesser extent, to other ions as well. Raymond & Doyle (1981a, 1981b) applied the ionisation equilibrium calculations of Vernazza & Raymond (1978) to Skylab data and found a good agreement between lines of different isoelectronic sequences. The problem appeared to be resolved.
However, the same authors (Doyle & Raymond 1984), among others, presented cases where these density effects were not enough to explain the anomalous behaviour. At that time, uncertainties in the atomic data and instrument's calibration were a major concern. Judge et al. (1995) presented a DEM analysis of a rocket spectrum of the entire Sun, obtained with a good photometric accuracy of 15%. They used more recent atomic data, and calculated the ionisation equilibrium taking into account the density effects. They found "very significant and systematic differences'' between the line intensities of the Li and Na isoelectronic sequences and those of the other ions. C IV, N V, and O VI lines were underestimated by factors of 2 to 5. Regarding the Na sequence, only Si IV was observed, with an underestimation by a factor of 2.
Another difficulty in investigating these effects was due to the fact that the majority of the strong lines that could be used for DEM analyses were from the anomalous class. For example, Raymond & Doyle (1981b) used Li-like lines (O VI, Ne VIII, Mg X, Si XII, S XIV), with the exception of Ar VII and Ca X, to constrain the million-degree peak of the DEM. The same argument applies to the Judge et al. (1995) results.
The problems of the paucity of the observed lines and uncertainty in the instrument's calibration have been overcomed with the spectroscopic instruments on board SOHO. Del Zanna (1999) has presented many DEM analyses of different solar regions, using SOHO/Coronal Diagnostic Spectrometer (CDS) spectra. The CDS instrument covers almost entirely the 150-800 Å spectral region, and is rich in emission lines from a large number of highly ionised ions of many different isoelectronic sequences. The CDS instrument has a good in-flight calibration (see Del Zanna et al. 2001a and references therein). The lines from the following ions have presented significant deviations (factors of 2 to 10): Ne VIII, Na IX, Mg X, Al XI, Si XII (Li-like); Ca X (Na-like). Del Zanna (1999) also found similar deviations with re-analyses of solar spectra from various instruments (including SERTS, Skylab). These discrepancies cannot be ascribed to elemental abundance anomalies, nor to instrumental effects.
Furthermore, progress in the theoretical models for ionisation and recombination processes has led to significant changes in the ionisation and recombination rates over the years. The compilation of Mazzotta et al. (1998) is the best available to date, computed for the low density limit. The Mazzotta et al. results have been used here. They are close to those of Arnaud & Raymond (1992) for the Fe ions. For the other elements the differences from the older calculations of Arnaud & Rothenflug (1985) are quite substantial, as discussed by Del Zanna (1999). Del Zanna et al. (2001b) have reanalysed Skylab data using the Mazzotta et al. (1998) ionisation fractions and up-to-date atomic data to show the extent of the anomalous behavior. The results are that lines of the Li-like N V and C IV are underestimated by factors of 3 and 10, while those of Ne VIII and Mg X are overestimated by factors of 5 and 10, respectively. The S VI 933.3 Å (Na-like) is also underestimated by a factor of 3.
We conclude that all the spectral lines of the Li and Na isoelectronic sequences observed in EUV solar spectra present significant deviations from other isoelectronic sequences. The analyses presented in Del Zanna (1999) also indicate a new characteristic. All lines in the lower transition region (e.g. C IV) are consistently underestimated, while those in the upper transition region (e.g. Ne VIII) are consistently overestimated. The deviations vary, depending on the source region observed. This suggests to us that one of the main inaccuracy in the ion balance calculations is the temperature corresponding to the peak emission. Until the reasons for these discrepancies are fully understood, and all the relevant physical effects taken into account, the lines of the Li and Na isoelectronic sequences should not be used for DEM, density and elemental abundance analyses.
Stellar coronal abundances are still poorly known, but are important to measure, because they affect our understanding of the stellar atmospheres. Comparisons with the solar case are difficult, since a large variety of solar coronal abundances have been reported, with variations from the photospheric values up to an order of magnitude (cf. the reviews of Feldman 1992; Raymond et al. 2001). These differences appear to be related to the first ionisation potential (FIP) of the various elements. The abundances of elements with low FIP (<10 eV, e.g. Fe) appear enhanced compared to those of the high FIP (>10 eV, e.g. Ne) elements, using the solar photospheric values as a standard reference. Sulfur is an important element since it lies in the middle of these two classes. This "FIP effect'' can be used as an important diagnostic of the physical processes that occur in the chromosphere and TR of active stars.
In principle,
it is possible to derive a relative element abundance
![]() of two elements X1 and X2 from any observed intensity ratio
of two elements X1 and X2 from any observed intensity ratio
![]() :
:
In the investigation of elemental abundances and the FIP effect it has been common to use ratios of low- vs. high-FIP lines that are emitted over the same temperature range and have similar contribution functions. In the solar case lines of Mg VI and Ne VI have been widely used. In the FUSE spectra the following ions present some temperature overlap: S III, S IV vs. N III; C III vs. N III; Si III vs. S III and C III; Ne VI vs. O VI; Ne V vs. S VI. The FUSE observations are complementary to those of Chandra and XMM, which observe coronal ions.
In the literature it is common to assume
that any intensity ratio is directly proportional to the
relative abundances of the two elements involved.
A common approach, proposed by Widing & Feldman (1989),
is to approximate Eq. (4) by defining
for each spectral line a single
differential emission measure
![]() value for
the temperature range over which the line forms:
value for
the temperature range over which the line forms:
The approach adopted here is to use the largest possible number of lines, calculate the line emissivities at the measured TR densities, and then determine the relative element abundances and the DEM(T) at the same time. The scaling between the high and low-FIP elements is done using lines that overlap in temperature. More details of the technique can be found in Del Zanna & Bromage (1999). In this way, most of the uncertainties will be reduced, and any systematic effects, such as those occurring with the Na- and Li-like lines will be highlighted. The use of line ratio methods for abundance diagnostics of solar and stellar coronae, in particular when lines of the Na and Li isoelectronic sequences are used, as recently suggested by e.g. Laming & Feldman (1999), is inadvisable.
The most accurate density diagnostics are those obtained by considering the ratios of lines emitted by the same ion which are sensitive to density. However, owing to the paucity of the observed density-sensitive line pairs from the same ion, other methods have often been adopted in solar and stellar physics. One method is to compare the emission measures of the forbidden lines with those of the allowed ones. One of the first applications of this method was due to Feldman et al. (1977). A variation of this method is to compare the emission measure loci of the two groups of lines, and is the most commonly used (see, e.g., Brown et al. 1984b; Byrne et al. 1987; Jordan et al. 1987; Linsky et al. 1989; Maran et al. 1994; Linsky et al. 1995; Griffiths & Jordan 1998; Pagano et al. 2000). In most cases, large inconsistencies between the densities obtained using this method with those derived from line ratios have been reported. These inconsistencies are caused by the use of lines with anomalous behaviour, as shown below in Sect. 5.3.
Diagnostics based on line ratios have been extensively used in solar and stellar physics. In many cases, discrepancies between densities derived using different line ratios or different ions have been reported, thus leading to suggestions that the derived values might not have any physical significance (Judge & McIntosh 1999). It is well known that significant effects on the line ratios can be caused by inhomogeneities in the atmosphere (see e.g., Doschek 1984) or by plasma flows (cf. Raymond & Dupree 1978). However, we would like to stress that some of these discrepancies could also be due to un-accounted blending and/or inaccurate atomic calculations, as shown below in Sect. 5.2 with some examples. In addition, that misleading results can easily be obtained by using line ratios that have a very small sensitivity at the observed densities or when temperature effects are not taken into account. In some cases, it is possible to obtain consistent measurements, although it should be born in mind that the derived densities are in any case averaged values over the entire stellar disk and along the line of sight.
Finally, it is common in the literature to use only
a few well-behaved line ratios, without considering all
the observed lines.
A different approach, preferable when more than two lines from an ion
are observed, is to plot the values of
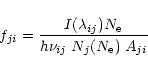 |
(9) |
Copyright ESO 2002