The dataset used was taken from the BATSE current catalogue. The
"discsc'' files are available at
http://www.batse.msfc.nasa.gov/batse/grb/catalog /4b/
(Paciesas et al. 1999). The files contain the data from the four
energy channels, which were combined into a single channel to
maximise the signal to noise ratio. The shapes of GRB pulses
vary little with energy and pulses in different energy channels
can be added together and nearly retain their initial shape. A
subset of the BATSE catalogue was selected based on the criteria
(Norris et al. 1996) that the GRB duration was greater than two
seconds (T90>2 s) and the peak flux
![]() photons cm-2 s-1. In this way a sample of 324 bursts
with good signal to noise and clearly resolved features was
obtained. Five of these bursts could not be analysed properly due
to data gaps, and so our final sample consisted of 319 GRBs. All
319 GRBs were used for the timing analyses. The 250 GRBs that
were summed over only two Large Area Detectors (LADs) were used for all
analyses involving pulse amplitude and area.
photons cm-2 s-1. In this way a sample of 324 bursts
with good signal to noise and clearly resolved features was
obtained. Five of these bursts could not be analysed properly due
to data gaps, and so our final sample consisted of 319 GRBs. All
319 GRBs were used for the timing analyses. The 250 GRBs that
were summed over only two Large Area Detectors (LADs) were used for all
analyses involving pulse amplitude and area.
The first step in the data preparation involved selecting the appropriate background for subtraction from the GRB. The start and end times for each burst were identified. A further margin of 10 s was added to both the beginning and end of this chosen section. Two background sections of duration 30 s were then selected, one finishing 20 s before the start of the section containing the burst and the other starting 20 s after the end of the burst (Fig. 1). These two regions were used to fit a linear background that was subtracted from the burst section.
One of the difficulties in analysing the time profiles of GRBs is in overcoming the limitations imposed by the presence of noise in the signal and the overlap of the individual pulses. The transient nature of GRBs also means that the usual assumptions for Fourier transform techniques do not hold (Chang & Yi 2000; Suzuki et al. 2001). An alternative method of filtering the signal is with wavelets. Wavelet analysis was pioneered by Daubechies (1992) and others during the 1980's (Meyer 1993).
Wavelets are specific functions that, when convolved with the signal under investigation, produce a transformed signal that represents the location and strength of variations within the original data. The convolution is applied repeatedly to the data over a range of scales with the convolution function gradually stretched to coarser and coarser scales, revealing variations at corresponding scales in the original signal. This iteration with scaling of the convolved function allows the identification of structure with a variety of extents both in the spatial and frequency domains.
If the wavelet function is written as ![]() then, more formally,
the transform of f(x) at a particular scale s, can be written as
then, more formally,
the transform of f(x) at a particular scale s, can be written as
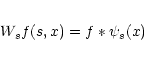
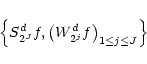
The function ![]() used in the algorithm was chosen so that
the wavelet acts like an edge detector with a delta response
function to a step edge. In fact
Wd2jf is proportional to
the derivative of the original signal smoothed at the scale 2j.
Thus calculating the positions of the modulus maxima of the
transform,
|Wd2J f|, is analogous to locating the sharp
variations in the original signal. Mallat & Zhong (1992) also
developed an algorithm for allowing the reconstruction of a
signal given just the modulus maxima of the wavelet transforms
across a set of scales along with the low frequency signal
remaining at the coarsest scale. This reduced representation can
reconstruct an accurate copy of the original, using an iterative
algorithm that converges quite quickly to acceptable levels.
used in the algorithm was chosen so that
the wavelet acts like an edge detector with a delta response
function to a step edge. In fact
Wd2jf is proportional to
the derivative of the original signal smoothed at the scale 2j.
Thus calculating the positions of the modulus maxima of the
transform,
|Wd2J f|, is analogous to locating the sharp
variations in the original signal. Mallat & Zhong (1992) also
developed an algorithm for allowing the reconstruction of a
signal given just the modulus maxima of the wavelet transforms
across a set of scales along with the low frequency signal
remaining at the coarsest scale. This reduced representation can
reconstruct an accurate copy of the original, using an iterative
algorithm that converges quite quickly to acceptable levels.
A technique for identifying white noise and removing it without
losing any other information was introduced by
Mallat & Hwang (1992). This technique relies on characterising the
behaviour of noise across the various scales in the wavelet
transform using just the information present in the extrema
wavelet representation described in the previous paragraph. The
change in the amplitude of the extrema between scales allows the
number called the Lipschitz exponent to be calculated. More
precisely, each extremum describes a particular curve in
![]() space representing its increase or decay on all
the scales for which Wf(s,x) has been computed. Then the
Lipschitz exponent,
space representing its increase or decay on all
the scales for which Wf(s,x) has been computed. Then the
Lipschitz exponent, ![]() ,
is just the maximum slope of a
straight line that remains above this curve (Young et al. 1995).
Using results from an analysis of white noise
(
,
is just the maximum slope of a
straight line that remains above this curve (Young et al. 1995).
Using results from an analysis of white noise
(
![]() ,
Mallat & Hwang 1992), as well as the
investigation described below, the characteristic distribution of
Lipschitz exponents for the noise present in BATSE GRB profiles
was determined. In general, noise is expected to have a negative
Lipschitz exponent indicating a decreasing amplitude with
increasing scale. Extrema in the wavelet transform which fall in
the range expected for noise can be removed using an algorithm
developed for this purpose.
,
Mallat & Hwang 1992), as well as the
investigation described below, the characteristic distribution of
Lipschitz exponents for the noise present in BATSE GRB profiles
was determined. In general, noise is expected to have a negative
Lipschitz exponent indicating a decreasing amplitude with
increasing scale. Extrema in the wavelet transform which fall in
the range expected for noise can be removed using an algorithm
developed for this purpose.
As an example consider the extremum at around 110 s on the top
(finest) scale of GRB 920513 (Fig. 2c). On the next scale, the
amplitude of this extremum is considerably smaller and by the
following scale it is hardly detectable. It is clear that this
extremum corresponds to a noise feature in the original signal and
visual examination of the transform indicates that the amplitude
of the wavelet transform decays quickly when moving to
progressively coarser scales, as expected for noise. The extremum
at around 95 s corresponds to a pulse with intensity over 25 000
counts per 64 ms. The amplitude of the wavelet maximum increases
on coarser scales, contrary to the behaviour expected for noise.
The extrema removal algorithm was combined with a simple
thresholding procedure based on the analysis of a section of the
burst background. For each burst being prepared, a section of the
same burst well separated from the signal was used to generate the
wavelet transform of the background. The standard deviation of the
transform at the scale 22 (the finest scale not dominated by
noise) was combined with a significance level (![]() )
to
calculate an amplitude threshold for the wavelet coefficients of
the signal at the same scale. Any extrema in the signal with
amplitudes less than this threshold on scale 22 were assumed to
be due to noise and were removed.
)
to
calculate an amplitude threshold for the wavelet coefficients of
the signal at the same scale. Any extrema in the signal with
amplitudes less than this threshold on scale 22 were assumed to
be due to noise and were removed.
A denoised signal was then reconstructed (e.g. Fig. 2a) using the algorithm described by Mallat & Zhong (1992). The reconstructed functions have no spurious oscillations or sharp variations, and are very similar to the original signal. The residuals between the background subtracted burst and the reconstructed burst are shown in Fig. 2b. The residuals were calculated assuming that the errors in the raw data were Poisson distributed. The variation of the residuals in the section containing signal do not differ significantly from a section due to background noise (Fig. 2b).
Each pulse was examined to find minima on each side which were
separated in amplitude from the maximum by more than a chosen
significance level. If the search for minima failed on a pulse it
was rejected and the search for pulses continued. The algorithm
was designed so that the maximum and minima finally selected for a
given pulse were the extreme values in that region of the signal.
The significance level of the maxima and minima was calculated by
multiplying the error on the counts by a scale factor,
![]() .
Given two data points n1 and n2, where
n1>n2, the points overlap if
.
Given two data points n1 and n2, where
n1>n2, the points overlap if
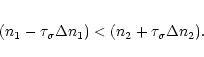
The pulse selection process is illustrated in Fig. 3. Starting with pulse 2, minima 1 and 3 were easily identified. Next, pulse 4 was considered. Pulse 4 overlaps the adjacent minimum 3 (based on appropriately sized error bars) and both turning points were rejected and minimum 5 was considered as the true minimum associated with pulse 2. A minimum, maximum, minimum triplet consisting of points 1, 2 and 5 was found. At the conclusion of the analysis the overlapping maxima/minima pairs consisting of points 6 and 7, 9 and 10 and 13 and 14 were rejected. The algorithm selected points 2, 8 and 12 as the maxima and identified associated minima 1, 5, 11 and 15.
The analysis was then extended to allow the identification of
pulses that were well separated from their neighbours such that
the overlap from the surrounding signal did not significantly
affect the profile of the pulse. The fraction of the total height,
![]() ,
(from pulse to background) which was above the higher
minimum was determined and a threshold was applied to this
fraction, above which pulses were considered isolated. In Fig. 3
the pulses 8 and 12 are not very well separated from their
neighbours whereas pulse 2 is effectively isolated and not
strongly influenced by surrounding signal. The fractional isolated
height of pulse 8 (to which the threshold is applied) was obtained
using (Fig. 3):
,
(from pulse to background) which was above the higher
minimum was determined and a threshold was applied to this
fraction, above which pulses were considered isolated. In Fig. 3
the pulses 8 and 12 are not very well separated from their
neighbours whereas pulse 2 is effectively isolated and not
strongly influenced by surrounding signal. The fractional isolated
height of pulse 8 (to which the threshold is applied) was obtained
using (Fig. 3):
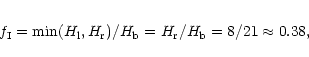
For pulse 2 (with point 1 being the higher minimum the smaller
height difference is on the left) the estimate is:
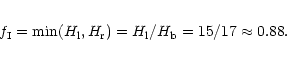
The next task was to characterise the GRB profiles based on the
properties of the constituent pulses. The following
characteristics which had been studied previously
(McBreen et al. 1994; Li & Fenimore 1996; Hurley et al. 1998) were investigated: the
number of pulses per burst, N; the time intervals between
pulses, ![]() ;
the pulse amplitudes, C; the pulse
area,
;
the pulse amplitudes, C; the pulse
area,
![]() ;
the rise and fall times,
;
the rise and fall times,
![]() and
and
![]() ;
and the pulse durations or full width at half
maximum, FWHM.
;
and the pulse durations or full width at half
maximum, FWHM.
The total number of pulses in the sample of 319 GRBs was
determined for a range of thresholds
![]() and
varying isolation levels,
and
varying isolation levels,
![]() (Fig. 4). The variation
in isolation level has a much larger effect on the sample than the
threshold, and caused a reduction in the number of pulses from
over 3000 at the isolation level of 20% to under 800 at the 80%
level. Figure 4 also shows that the number of pulses falls quite
quickly as
(Fig. 4). The variation
in isolation level has a much larger effect on the sample than the
threshold, and caused a reduction in the number of pulses from
over 3000 at the isolation level of 20% to under 800 at the 80%
level. Figure 4 also shows that the number of pulses falls quite
quickly as
![]() increases from 3 to 5. The
initial rapid reduction in the number of pulses selected may be an
indication of the removal of the small population of noise pulses
remaining after the denoising process. The total number of
pulses is not very sensitive to the threshold level in the region
of 5
increases from 3 to 5. The
initial rapid reduction in the number of pulses selected may be an
indication of the removal of the small population of noise pulses
remaining after the denoising process. The total number of
pulses is not very sensitive to the threshold level in the region
of 5
![]() .
The 319 GRBs are listed in Table 1, along with
the total number of pulses above 5
.
The 319 GRBs are listed in Table 1, along with
the total number of pulses above 5
![]() for each burst.
Also included in the table are the number of isolated pulses at
and above the 50% and 75% levels.
for each burst.
Also included in the table are the number of isolated pulses at
and above the 50% and 75% levels.
| GRB | N | N(50/75) | GRB | N | N(50/75) | GRB | N | N(50/75) | GRB | N | N(50/75) | GRB | N | N(50/75) | GRB | N | N(50/75) |
| 105 | 4 | 3/2 | 1974 | 2 | 0/0 | 2994 | 36 | 20/6 | 3929 | 3 | 2/1 | 6113 | 5 | 3/1 | 7318 | 12 | 5/3 |
| 109 | 19 | 10/2 | 1997 | 13 | 8/2 | 3001 | 3 | 3/2 | 3930 | 19 | 6/1 | 6124 | 30 | 14/5 | 7329 | 3 | 0/0 |
| 130 | 11 | 5/1 | 2037 | 6 | 5/3 | 3035 | 21 | 4/1 | 3936 | 5 | 1/1 | 6168 | 2 | 1/1 | 7343 | 11 | 2/1 |
| 143 | 13 | 6/3 | 2053 | 1 | 1/1 | 3039 | 5 | 3/1 | 3954 | 1 | 1/1 | 6198 | 10 | 1/1 | 7360 | 5 | 4/1 |
| 179 | 4 | 3/2 | 2067 | 8 | 1/1 | 3042 | 19 | 12/6 | 4039 | 33 | 21/7 | 6235 | 6 | 3/1 | 7374 | 1 | 1/1 |
| 219 | 13 | 4/3 | 2080 | 26 | 12/2 | 3057 | 52 | 3/1 | 4048 | 9 | 3/3 | 6242 | 3 | 3/3 | 7429 | 3 | 1/1 |
| 222 | 6 | 0/0 | 2083 | 2 | 2/1 | 3067 | 8 | 4/3 | 4312 | 4 | 2/1 | 6251 | 3 | 3/2 | 7446 | 1 | 1/1 |
| 249 | 21 | 4/1 | 2090 | 15 | 7/2 | 3105 | 30 | 19/9 | 4368 | 12 | 2/2 | 6266 | 9 | 2/1 | 7464 | 3 | 2/1 |
| 394 | 25 | 13/3 | 2110 | 13 | 3/1 | 3110 | 13 | 8/3 | 4556 | 3 | 1/1 | 6274 | 18 | 16/6 | 7475 | 2 | 2/2 |
| 451 | 2 | 2/2 | 2138 | 6 | 2/2 | 3115 | 9 | 6/3 | 4701 | 20 | 8/4 | 6303 | 1 | 1/1 | 7477 | 9 | 3/2 |
| 467 | 3 | 1/1 | 2151 | 3 | 3/3 | 3128 | 36 | 13/1 | 4814 | 2 | 1/1 | 6321 | 3 | 3/3 | 7491 | 40 | 11/1 |
| 469 | 1 | 1/1 | 2156 | 39 | 8/3 | 3138 | 4 | 2/1 | 5080 | 7 | 7/3 | 6329 | 9 | 1/1 | 7503 | 4 | 1/1 |
| 503 | 1 | 1/1 | 2213 | 5 | 5/2 | 3178 | 6 | 3/1 | 5304 | 14 | 0/0 | 6335 | 2 | 2/2 | 7527 | 2 | 2/2 |
| 543 | 3 | 2/1 | 2228 | 28 | 12/5 | 3227 | 17 | 5/3 | 5389 | 13 | 7/3 | 6336 | 3 | 0/0 | 7529 | 1 | 1/1 |
| 647 | 3 | 1/1 | 2232 | 14 | 8/6 | 3241 | 15 | 10/3 | 5417 | 2 | 0/0 | 6397 | 1 | 1/1 | 7530 | 2 | 2/2 |
| 660 | 2 | 2/1 | 2316 | 1 | 1/1 | 3245 | 71 | 24/6 | 5419 | 2 | 1/1 | 6400 | 3 | 3/3 | 7549 | 33 | 6/2 |
| 676 | 4 | 2/1 | 2321 | 11 | 4/1 | 3255 | 12 | 6/3 | 5439 | 4 | 4/3 | 6404 | 13 | 7/2 | 7560 | 12 | 8/6 |
| 678 | 52 | 21/6 | 2329 | 20 | 3/1 | 3269 | 15 | 13/7 | 5447 | 2 | 1/1 | 6413 | 8 | 7/3 | 7575 | 30 | 10/4 |
| 829 | 3 | 0/0 | 2362 | 2 | 2/2 | 3287 | 10 | 6/1 | 5450 | 13 | 5/4 | 6422 | 2 | 0/0 | 7605 | 9 | 9/3 |
| 841 | 6 | 6/3 | 2367 | 3 | 3/2 | 3290 | 6 | 4/3 | 5451 | 2 | 0/0 | 6436 | 3 | 3/3 | 7607 | 8 | 8/3 |
| 869 | 10 | 4/1 | 2371 | 2 | 2/1 | 3306 | 16 | 13/4 | 5470 | 7 | 4/4 | 6451 | 3 | 2/1 | 7678 | 37 | 5/2 |
| 907 | 4 | 3/2 | 2387 | 1 | 1/1 | 3330 | 13 | 5/3 | 5473 | 39 | 27/19 | 6453 | 25 | 5/1 | 7688 | 14 | 9/3 |
| 973 | 3 | 1/1 | 2393 | 2 | 1/1 | 3345 | 4 | 1/1 | 5477 | 12 | 9/5 | 6472 | 47 | 18/5 | 7695 | 27 | 16/5 |
| 999 | 2 | 2/2 | 2431 | 1 | 1/1 | 3351 | 10 | 7/5 | 5486 | 12 | 1/1 | 6525 | 8 | 6/5 | 7711 | 1 | 1/1 |
| 1025 | 4 | 2/1 | 2436 | 11 | 8/2 | 3408 | 44 | 17/5 | 5489 | 16 | 8/4 | 6528 | 8 | 3/1 | 7766 | 22 | 15/6 |
| 1085 | 2 | 0/0 | 2446 | 4 | 3/2 | 3415 | 14 | 8/4 | 5512 | 5 | 1/1 | 6560 | 20 | 16/9 | 7770 | 3 | 2/1 |
| 1122 | 10 | 3/1 | 2450 | 22 | 7/4 | 3436 | 5 | 4/1 | 5523 | 2 | 2/2 | 6576 | 18 | 11/5 | 7775 | 1 | 1/1 |
| 1141 | 9 | 0/0 | 2533 | 49 | 9/1 | 3458 | 8 | 2/2 | 5526 | 34 | 34/14 | 6587 | 28 | 9/4 | 7781 | 4 | 2/2 |
| 1157 | 10 | 8/2 | 2537 | 5 | 2/1 | 3480 | 1 | 1/1 | 5530 | 7 | 5/1 | 6593 | 20 | 13/2 | 7788 | 21 | 14/6 |
| 1159 | 1 | 1/1 | 2586 | 11 | 7/7 | 3481 | 11 | 1/1 | 5548 | 9 | 8/4 | 6621 | 2 | 2/2 | 7845 | 17 | 15/11 |
| 1190 | 4 | 2/2 | 2611 | 3 | 2/2 | 3488 | 6 | 6/5 | 5563 | 1 | 1/1 | 6629 | 6 | 4/3 | 7858 | 5 | 0/0 |
| 1204 | 3 | 3/3 | 2628 | 7 | 5/2 | 3489 | 12 | 2/2 | 5567 | 5 | 1/1 | 6630 | 2 | 1/1 | 7884 | 21 | 15/6 |
| 1385 | 23 | 4/1 | 2700 | 4 | 3/1 | 3491 | 3 | 1/1 | 5568 | 3 | 0/0 | 6665 | 8 | 2/1 | 7906 | 13 | 7/5 |
| 1419 | 3 | 1/1 | 2736 | 1 | 1/1 | 3512 | 1 | 1/1 | 5572 | 3 | 3/3 | 6672 | 4 | 3/1 | 7929 | 6 | 4/1 |
| 1425 | 7 | 5/1 | 2790 | 20 | 10/1 | 3516 | 10 | 7/2 | 5575 | 6 | 2/1 | 6683 | 10 | 10/3 | 7954 | 16 | 14/13 |
| 1440 | 15 | 9/2 | 2793 | 7 | 4/3 | 3523 | 16 | 0/0 | 5591 | 10 | 7/4 | 6694 | 10 | 6/1 | 7969 | 2 | 1/1 |
| 1443 | 2 | 2/2 | 2797 | 3 | 1/1 | 3569 | 4 | 2/2 | 5593 | 1 | 1/1 | 6764 | 8 | 3/1 | 7987 | 6 | 2/1 |
| 1468 | 19 | 17/6 | 2798 | 11 | 1/1 | 3593 | 13 | 6/1 | 5601 | 1 | 1/1 | 6814 | 1 | 1/1 | 7994 | 13 | 1/1 |
| 1533 | 32 | 20/12 | 2799 | 8 | 6/6 | 3598 | 3 | 3/2 | 5614 | 2 | 2/2 | 6816 | 8 | 7/3 | 7998 | 4 | 3/2 |
| 1541 | 33 | 11/1 | 2812 | 15 | 12/9 | 3634 | 7 | 7/3 | 5621 | 6 | 3/1 | 6824 | 2 | 2/2 | 8008 | 6 | 3/3 |
| 1578 | 3 | 0/0 | 2831 | 58 | 12/2 | 3648 | 3 | 3/1 | 5628 | 9 | 4/1 | 6904 | 1 | 1/1 | 8019 | 2 | 2/1 |
| 1606 | 33 | 15/4 | 2852 | 23 | 5/1 | 3649 | 2 | 2/2 | 5644 | 4 | 1/1 | 6930 | 2 | 2/2 | 8022 | 5 | 5/4 |
| 1609 | 8 | 2/1 | 2855 | 13 | 2/1 | 3658 | 4 | 2/1 | 5654 | 5 | 3/2 | 6963 | 17 | 10/2 | 8030 | 7 | 6/3 |
| 1625 | 15 | 2/1 | 2856 | 86 | 19/3 | 3663 | 9 | 7/3 | 5704 | 9 | 8/4 | 7028 | 5 | 3/2 | 8050 | 1 | 1/1 |
| 1652 | 6 | 1/1 | 2889 | 26 | 12/4 | 3765 | 4 | 2/2 | 5711 | 2 | 2/1 | 7113 | 52 | 8/1 | 8063 | 4 | 4/3 |
| 1663 | 16 | 0/0 | 2891 | 18 | 15/4 | 3776 | 7 | 1/1 | 5725 | 13 | 12/6 | 7170 | 16 | 6/2 | 8087 | 8 | 7/3 |
| 1664 | 5 | 1/1 | 2894 | 5 | 1/1 | 3788 | 4 | 3/1 | 5726 | 3 | 3/1 | 7172 | 1 | 1/1 | 8098 | 4 | 2/2 |
| 1676 | 35 | 21/7 | 2913 | 5 | 2/2 | 3860 | 13 | 9/3 | 5773 | 4 | 1/1 | 7185 | 19 | 16/7 | 8099 | 1 | 1/1 |
| 1683 | 6 | 3/1 | 2919 | 3 | 3/2 | 3866 | 1 | 1/1 | 5867 | 7 | 6/3 | 7240 | 4 | 4/4 | 8111 | 2 | 2/1 |
| 1709 | 2 | 0/0 | 2929 | 44 | 16/5 | 3870 | 1 | 1/1 | 5955 | 4 | 2/2 | 7247 | 2 | 1/1 | |||
| 1711 | 8 | 2/1 | 2953 | 6 | 2/2 | 3891 | 3 | 2/1 | 5989 | 8 | 7/5 | 7255 | 5 | 1/1 | |||
| 1815 | 10 | 5/2 | 2958 | 2 | 2/2 | 3893 | 3 | 1/1 | 5995 | 7 | 1/1 | 7290 | 1 | 1/1 | |||
| 1883 | 1 | 1/1 | 2984 | 22 | 16/6 | 3905 | 4 | 4/1 | 6090 | 3 | 1/1 | 7301 | 51 | 13/7 | |||
| 1886 | 5 | 0/0 | 2988 | 2 | 2/2 | 3912 | 1 | 1/1 | 6100 | 3 | 0/0 | 7305 | 3 | 3/3 |
![\begin{figure}
\par\includegraphics[angle=90,width=12.5cm,clip]{h3056f7.eps} %
\end{figure}](/articles/aa/full/2002/14/aah3056/Timg48.gif) |
Figure 5:
The distribution of the number of pulses (N) per GRB.
The shaded regions highlight the division into four
categories, namely M, N, O and P with
|
In the analysis of pulse shapes, non-parametric methods were used
to estimate the various characteristics of the pulse profiles.
This approach was chosen to make the conclusions more robust since
no assumptions were made about the pulse shapes. Also since the
measurements are made on the isolated pulses selected by the
algorithm, the degree of isolation can be varied arbitrarily. If a
particular measurement was sensitive to influence from surrounding
pulses then the threshold
![]() was increased until the
influence was reduced sufficiently, with the proviso that the
number of pulses in the sample remains statistically useful.
was increased until the
influence was reduced sufficiently, with the proviso that the
number of pulses in the sample remains statistically useful.
The classification of pulses into isolated and non-isolated
categories based on the algorithm allowed the measurement of
characteristics of the temporal profile which are affected by
neighbouring signals. The level of interference between pulses and
the surrounding signal is dependent on the threshold at which the
selection of these pulses is made. In fact a broad range of
threshold levels were used to examine the time profiles and
![]() was typically varied from 20% to 80%. It was decided
based on these results to adopt pulses with
was typically varied from 20% to 80%. It was decided
based on these results to adopt pulses with
![]() and
and
![]() for
the main analysis of the pulse properties.
for
the main analysis of the pulse properties.
The pulse amplitude was measured as the maximum count in a 64 ms time interval after background subtraction. The pulse area was measured using the sum of the background subtracted count rates starting at 5% of the height of the pulse above the left minimum to 5% of the pulse height above the right minimum on the falling edge of the profile. The starting point at 5% above the minimum was chosen to eliminate contributions from background noise for pulses with minima widely separated from the maximum.
For similar reasons the rise time was measured from 5% of the height of the pulse above the left minimum to 95% of that height. The upper value of 95% ensures that the finishing point is robust against flat topped pulses and noise in the profile near the maximum. The fall time was measured in a similar way to the rise times i.e. from 95% to 5% of the pulse height above the right minimum.
The duration of the individual pulses was measured using the FWHM of the pulse. This approximation is valid only for well isolated pulses and tended to give poorer estimates for the true pulse width as the effect of neighbouring signals increased and the left and right minima of the pulse rose out of the background.
The frequency distribution of the number of pulses (N) per GRB is
given in Fig. 5. N has a range from 1 to 86 with a peak at a
value of 3, a median of 6 and only 10% of GRBs have ![]() .
For convenience N is divided into four categories (Fig. 5). There
are 34 GRBs in category P and only 7 have N > 50. Many of the
timing studies on GRBs have concentrated on the categories with
large N (e.g. Norris et al. 1996; Li & Fenimore
1996), which means that these
analyses have focussed solely on the tail of the distribution
shown in Fig. 5.
.
For convenience N is divided into four categories (Fig. 5). There
are 34 GRBs in category P and only 7 have N > 50. Many of the
timing studies on GRBs have concentrated on the categories with
large N (e.g. Norris et al. 1996; Li & Fenimore
1996), which means that these
analyses have focussed solely on the tail of the distribution
shown in Fig. 5.
Copyright ESO 2002