Rotation plays a central role in the atmospheric dynamics of
Pegasi planets, and HD 209458b in particular. The ratio of nonlinear
advective accelerations
to Coriolis accelerations in the horizontal momentum equation is
u f-1 L-1 (called the Rossby number), where
u is the mean horizontal wind speed,
![]() is
the "Coriolis parameter'' (e.g. Holton 1992, pp. 39-40),
is
the "Coriolis parameter'' (e.g. Holton 1992, pp. 39-40), ![]() is the rotational angular velocity,
is the rotational angular velocity, ![]() is latitude, and Lis a characteristic length scale. Rossby numbers of 0.03-0.3
are expected for winds of planetary-scale and speeds ranging
from
is latitude, and Lis a characteristic length scale. Rossby numbers of 0.03-0.3
are expected for winds of planetary-scale and speeds ranging
from
![]() .
In Sect. 3 we showed that modest
asynchronous rotation may occur, in which case the Rossby number could
differ from this estimate by a factor up to
.
In Sect. 3 we showed that modest
asynchronous rotation may occur, in which case the Rossby number could
differ from this estimate by a factor up to ![]() 2.
These estimates suggest that nonlinear advective terms are small compared
to the Coriolis accelerations, which must then
balance with the pressure-gradient accelerations.
(The Rossby number could be
2.
These estimates suggest that nonlinear advective terms are small compared
to the Coriolis accelerations, which must then
balance with the pressure-gradient accelerations.
(The Rossby number could be ![]() 1 if the winds reach
1 if the winds reach
![]() ,
which we show below is probably the maximum
allowable wind speed.)
,
which we show below is probably the maximum
allowable wind speed.)
| u | R | Jet width | ||||
|
|
(
|
(
|
(
|
(
|
(
|
|
| Jupiter | 50 | 7.1 | 1.74 | 1.0 | 0.2 | |
| Saturn | 200 | 6.0 | 1.6 | 1.9 | 0.2 | |
| Uranus | 300 | 2.6 | 1.0 | 2.0 | 0.2 | |
| Netpune | 300 | 2.5 | 1.1 | 1.9 | 0.2 | |
| HD 209458b | ? | 10 | 15(u/1 km s -1)1/2 | ? |
Note. ![]() calculated at the tropopause using
calculated at the tropopause using
![]() for Saturn, Uranus, and Neptune, and
for Saturn, Uranus, and Neptune, and
![]() for Jupiter.
for Jupiter.
The zonality of the flow can be characterized by the Rhines'
wavenumber,
![]() ,
where
,
where ![]() is the derivative of f with
northward distance (Rhines 1975). The
half-wavelength implied by this wavenumber, called the Rhines'
scale
is the derivative of f with
northward distance (Rhines 1975). The
half-wavelength implied by this wavenumber, called the Rhines'
scale ![]() ,
provides a
reasonable estimate for the jet widths on all four outer planets
in our solar system (Cho & Polvani 1996; see Table 1).
For HD 209458b, the Rhines' scale is
,
provides a
reasonable estimate for the jet widths on all four outer planets
in our solar system (Cho & Polvani 1996; see Table 1).
For HD 209458b, the Rhines' scale is
![]() ,
which exceeds the planetary radius if
the wind speed exceeds about
,
which exceeds the planetary radius if
the wind speed exceeds about
![]() .
.
Another measure of horizontal structure is
the Rossby deformation radius (Gill 1982, p. 205),
![]() ,
where H is the scale height and N is the Brünt-Vaisala
frequency (i.e., the oscillation frequency for a vertically displaced
air parcel; Holton 1992, p. 54).
At pressures of a few bars, the temperature profiles
calculated for irradiated extrasolar giant planets by Goukenlouque
et al. (2000) suggest
,
where H is the scale height and N is the Brünt-Vaisala
frequency (i.e., the oscillation frequency for a vertically displaced
air parcel; Holton 1992, p. 54).
At pressures of a few bars, the temperature profiles
calculated for irradiated extrasolar giant planets by Goukenlouque
et al. (2000) suggest
![]() .
With a scale height
of 700 km, the resulting deformation radius is 40000 km. In contrast,
the deformation radii near the tropopause of Jupiter, Saturn,
Uranus, and Neptune are of order 2000 km (Table 1).
.
With a scale height
of 700 km, the resulting deformation radius is 40000 km. In contrast,
the deformation radii near the tropopause of Jupiter, Saturn,
Uranus, and Neptune are of order 2000 km (Table 1).
The estimated Rhines' scale (for winds of
![]() ,
which we
show later are plausible speeds) and deformation radius of Pegasi planets
,
which we
show later are plausible speeds) and deformation radius of Pegasi planets![]() are similar to the planetary radius, and they are
a larger fraction of the planetary radius than is the case for
Jupiter, Saturn, Uranus, and Neptune (Table 1). This fact suggests that
eddies may grow to hemispheric scale in the atmospheres of
Pegasi planets
are similar to the planetary radius, and they are
a larger fraction of the planetary radius than is the case for
Jupiter, Saturn, Uranus, and Neptune (Table 1). This fact suggests that
eddies may grow to hemispheric scale in the atmospheres of
Pegasi planets![]() and that, compared with the giant planets in our
solar system, the general circulation hot Jupiters may be more
global in character. Unless the winds are extremely weak, Pegasi planets
and that, compared with the giant planets in our
solar system, the general circulation hot Jupiters may be more
global in character. Unless the winds are extremely weak, Pegasi planets![]() are unlikely to have >10 jets as do Jupiter and Saturn.
are unlikely to have >10 jets as do Jupiter and Saturn.
An upper limit on the atmospheric wind speed can be derived from
shear-instability considerations. We assume that no zonal winds are
present (u(P0)=0) in the convective core, a consequence of
synchronization by tidal friction.
The build-up of winds at higher altitudes in the radiative envelope
is suppressed by Kelvin-Helmholtz instabilities
if the shear becomes too large. This occurs
when the Richardson number becomes smaller than 1/4 (cf. Chandrasekhar
1961), i.e. when
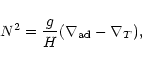 |
(8) |
The maximal wind speed at which Kelvin-Helmholtz instabilities occur
can then be derived by integration of Eq. (7):
![\begin{displaymath}u_{\rm max}(P)\sim {1\over 2}\int_{P_0}^{P}
\left[{\cal R}T(\nabla_{\rm ad}-\nabla_T)\right]^{1/2} {\rm d}\ln p.
\end{displaymath}](/articles/aa/full/2002/13/aa1885/img79.gif) |
(9) |
A characteristic timescale for zonal winds to redistribute temperature
variations over scales similar to the planetary radius Rthen stems from
![]() .
.
The radiative heating timescale can be estimated by a ratio between the
thermal energy within a given layer and the layer's net radiated flux.
In the absence of dynamics, absorbed solar fluxes balance the
radiated flux, but dynamics perturbs the temperature profile away from
radiative equilibrium. Suppose the radiative equilibrium temperature at
a particular location is
![]() and the actual temperature
is
and the actual temperature
is
![]() .
At levels close to optical depth unity,
the net flux radiated towards outer space is then
.
At levels close to optical depth unity,
the net flux radiated towards outer space is then
![]() and the radiative timescale is
and the radiative timescale is
Figure 4 shows estimates of
![]() and
and
![]() for HD 209458b
calculated using the temperature profiles from the
"hot'' (thin line) and "cold'' (thick grey line) models from Sect. 2.
The zonal timescale is estimated by calculating the maximum wind speed that can
exist as a function of pressure given the static stability associated with
each model, while the radiative time is calculated using the
temperatures and heat capacities shown in Fig. 1.
At pressures exceeding 0.1bar, radiation is
slower than the maximal advection by zonal winds, but by less than one
order of magnitude. The consequent day/night temperature difference
for HD 209458b
calculated using the temperature profiles from the
"hot'' (thin line) and "cold'' (thick grey line) models from Sect. 2.
The zonal timescale is estimated by calculating the maximum wind speed that can
exist as a function of pressure given the static stability associated with
each model, while the radiative time is calculated using the
temperatures and heat capacities shown in Fig. 1.
At pressures exceeding 0.1bar, radiation is
slower than the maximal advection by zonal winds, but by less than one
order of magnitude. The consequent day/night temperature difference
![]() to
be expected is:
to
be expected is:
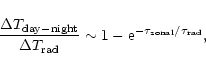 |
(11) |
The small radiative time scale implies that, for the day-night
temperature difference to be negligible near the planet's photosphere,
atmospheric winds would have to be larger than the maximum winds for
the onset of shear instabilities.
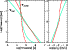 |
Figure 4:
Left: characteristic time scales as a function of pressure level.
|
An understanding of the horizontal temperature difference and
mean wind speed is desirable. It is furthermore of interest to
clarify the possible geometries the flow may take. For Pegasi planets,
we envision that the dominant forcing is the large-scale
day-night heating contrast, with minimal role for moist convection.
This situation differs from that of Jupiter, where differential escape of the
intrinsic heat flux offsets the solar heating contrast and moist convection
plays a key role. For Pegasi planets, such an offset between intrinsic and
stellar fluxes cannot occur, because the intrinsic flux is 104times less than
the total flux. The fact that the day-night heating
contrast occurs at hemispheric scale - and that the
relevant dynamical length
scales for Pegasi planets![]() are also hemispheric (Sect. 4.1) - increases our
confidence that
simple analysis, focusing on the hemispheric-scale circulation, can
provide insight.
are also hemispheric (Sect. 4.1) - increases our
confidence that
simple analysis, focusing on the hemispheric-scale circulation, can
provide insight.
Because the Rossby number is small, the dominant balance in the horizontal
momentum equation at mid-latitudes
is between the Coriolis force and the pressure-gradient force
(geostrophic balance).
We adopt the primitive equations, which are the standard set of large-scale
dynamical equations in a stably-stratified planetary atmosphere.
When differentiated with pressure (which is used here as a vertical
coordinate), this balance leads to the well-known
thermal wind equation (e.g. Holton 1992, p. 75):
The thermodynamic energy equation is, using pressure as a vertical
coordinate (e.g. Holton 1992, p. 60),
A priori, it is unclear whether the radiative heating and cooling is dominantly balanced by horizontal advection (second term on left of Eq. (14)) or vertical advection (third term on the left). To illustrate the possibilities, we consider two endpoint scenarios corresponding to the two limits. In the first scenario, the radiation is balanced purely by horizontal advection: zonal winds transport heat from dayside to nightside, and meridional winds transport heat from equator to pole. In the second scenario, the radiation is balanced by vertical advection (ascent on dayside, descent on nightside).
Consider the first scenario, where horizontal
advection dominates. Generally, we expect ![]() and
and
![]() to point in different directions, and to order of magnitude
their dot product
equals the product of their magnitudes. (If the direction of
to point in different directions, and to order of magnitude
their dot product
equals the product of their magnitudes. (If the direction of
![]() is independent of height and no deep
barotropic flow exists, then at mid-latitudes one could argue that winds
and horizontal pressure gradients are perpendicular to order Ro.
However, the existence of either asynchronous rotation or variations
in the orientations of
is independent of height and no deep
barotropic flow exists, then at mid-latitudes one could argue that winds
and horizontal pressure gradients are perpendicular to order Ro.
However, the existence of either asynchronous rotation or variations
in the orientations of
![]() with height will imply
that winds and
with height will imply
that winds and
![]() are not perpendicular even if
are not perpendicular even if
![]() .
Because asynchronous rotation and variation
in the directions of
.
Because asynchronous rotation and variation
in the directions of
![]() with height are likely,
and because, in any case,
with height are likely,
and because, in any case, ![]() and
and
![]() will not be
perpendicular near the equator, we write the dot product as the
product of the magnitudes.) An order-of-magnitude form of the
energy equation is then
will not be
perpendicular near the equator, we write the dot product as the
product of the magnitudes.) An order-of-magnitude form of the
energy equation is then
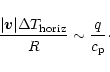 |
(15) |
The key difficulty in applying the equations to Pegasi planets![]() is the fact that
is the fact that
![]() depends on pressure, and
depends on pressure, and
![]() probably should too,
but Eqs. (16) and (17) were derived assuming that
probably should too,
but Eqs. (16) and (17) were derived assuming that
![]() is constant.
We can still obtain rough estimates by inserting values of
is constant.
We can still obtain rough estimates by inserting values of
![]() at several pressures. At
at several pressures. At ![]() 50-100 bars, where
50-100 bars, where
![]() ,
we obtain temperature
differences and wind speeds of 50-
,
we obtain temperature
differences and wind speeds of 50-![]() and 200-
and 200-
![]() .
At 1 bar, where
.
At 1 bar, where
![]() reaches
reaches
![]() ,
the estimated
temperature contrast and wind speed is
,
the estimated
temperature contrast and wind speed is ![]()
![]() and
and ![]()
![]() .
The estimates all assume
.
The estimates all assume
![]() ,
,
![]() ,
and
,
and
![]() .
.
Later we show that the equations successfully predict the mean wind speeds and temperature differences obtained in numerical simulations of the circulation of HD 209458b. This gives us confidence in the results.
Now consider
the second scenario, where vertical advection (third term on the left of
Eq. (14)) balances the radiative heating and cooling.
The magnitude of ![]() can be estimated from the continuity equation.
Purely geostrophic flow has zero horizontal divergence, so
can be estimated from the continuity equation.
Purely geostrophic flow has zero horizontal divergence, so ![]() is
roughly
is
roughly
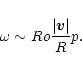 |
(19) |
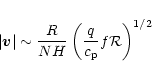 |
(20) |
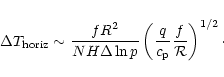 |
(21) |
We can estimate the vertical velocity under the assumption that
vertical advection balances the heating. Expressing the vertical
velocity w as the time derivative of an air parcel's altitude,
and using
![]() ,
where
,
where ![]() is density,
yields
is density,
yields
The numerical estimates, while rough, suggest that
winds could approach the upper limit of ![]()
![]() implied by the shear instability criterion. This comparison suggests
that Kelvin-Helmholtz shear instabilities may play an important role
in the dynamics.
implied by the shear instability criterion. This comparison suggests
that Kelvin-Helmholtz shear instabilities may play an important role
in the dynamics.
The likelihood of strong temperature contrasts can also be seen from
energetic considerations. The differential
stellar heating produces available
potential energy (i.e., potential energy that can
be converted to kinetic energy through rearrangement of the fluid;
Peixoto & Oort 1992, pp. 365-370), and in steady-state, this
potential energy must be converted to kinetic energy at the rate it
is produced. This requires
pressure gradients, which only exist in the presence of lateral
thermal gradients. A crude estimate suggests that the rate of
change of the difference in gravitational potential ![]() between
the dayside and nightside on isobars caused
by the heating is
between
the dayside and nightside on isobars caused
by the heating is
![]()
![]() .
The rate per mass at which potential
energy is converted to kinetic energy by pressure-gradient work
is
.
The rate per mass at which potential
energy is converted to kinetic energy by pressure-gradient work
is
![]() ,
which is approximately
,
which is approximately
![]() .
Equating the two
expressions
suggests, crudely, that
.
Equating the two
expressions
suggests, crudely, that
![]() ,
which implies
,
which implies
![]() using the values of
using the values of
![]() and
and
![]() near 1 bar discussed earlier.
near 1 bar discussed earlier.
One could wonder whether a possible flow geometry consists of dayside upwelling, nightside downwelling, and simple acceleration of the flow from dayside to nightside elsewhere (leading to a flow symmetrical about the subsolar point). The low-Rossby-number considerations described above argue against this scenario. A major component of the flow must be perpendicular to horizontal pressure gradients. Direct acceleration of wind from dayside to nightside is still possible near the equator, however. This would essentially be an equatorially-confined Walker-type circulation that, as described earlier, would lie equatorward of the geostrophic flows that exist at more poleward latitudes.
To better constrain the nature of the circulation, we performed
preliminary three-dimensional, fully-nonlinear numerical simulations
of the atmospheric circulation of HD 209458b. For the calculations, we used
the Explicit Planetary Isentropic Coordinate, or EPIC, model
(Dowling et al. 1998). The model solves the primitive equations
in spherical geometry using finite-difference methods and
isentropic vertical coordinates. The equations are valid in
stably-stratified atmospheres, and we solved the equations within
the radiative layer from 0.01 to 100 bars assuming the planet's
interior is in synchronous rotation with the 3.5-day orbital period.
The radius, surface gravity,
and rotation rate of HD 209458b were used (
![]() ,
,
![]() ,
and
,
and
![]() ,
respectively).
,
respectively).
The
intense insolation was parameterized with a simple
Newtonian heating scheme, which relaxes the temperature toward
an assumed radiative-equilibrium temperature profile. The
chosen radiative-equilibrium temperature profile was hottest
at the substellar point (![]() latitude,
latitude, ![]() longitude)
and decreased toward the nightside.
At the substellar point, the profile's height-dependence was
isothermal at 550 K
at pressures less than 0.03 bars and had
constant Brunt-Vaisala frequency of
longitude)
and decreased toward the nightside.
At the substellar point, the profile's height-dependence was
isothermal at 550 K
at pressures less than 0.03 bars and had
constant Brunt-Vaisala frequency of
![]() at pressures
exceeding 0.03 bars,
implying that the temperature increased with depth. The nightside
radiative-equilibrium temperature profile was equal to the
substellar profile minus
at pressures
exceeding 0.03 bars,
implying that the temperature increased with depth. The nightside
radiative-equilibrium temperature profile was equal to the
substellar profile minus ![]() ;
it is this day-night difference
that drives all the dynamics in the simulation. The
nightside profile was constant across the nightside, and the
dayside profile varied as
;
it is this day-night difference
that drives all the dynamics in the simulation. The
nightside profile was constant across the nightside, and the
dayside profile varied as
 |
(23) |
The Newtonian heating scheme described above is, of course, a
simplification. The day-night difference in radiative-equilibrium
temperature, 100 K, is smaller than the expected value. Furthermore,
the radiative timescale is too long in the upper troposphere
(![]() 0.1-1bar) and too short at deeper pressures
of
0.1-1bar) and too short at deeper pressures
of
![]() bars. Nevertheless, the net column-integrated heating
per area produced by the scheme (
bars. Nevertheless, the net column-integrated heating
per area produced by the scheme (
![]() )
is similar to that
expected to occur in the deep troposphere of HD 209458b and other
Pegasi planets, and the
simulation provides insight into the circulation patterns that
can be expected.
)
is similar to that
expected to occur in the deep troposphere of HD 209458b and other
Pegasi planets, and the
simulation provides insight into the circulation patterns that
can be expected.
The temperature used as the initial condition was isothermal at 500 K
at pressures less than 0.03 bars and had a constant Brunt-Vaisala
frequency of
![]() at pressures exceeding 0.03 bars.
There were no initial winds. The simulations were performed with
a horizontal resolution of
at pressures exceeding 0.03 bars.
There were no initial winds. The simulations were performed with
a horizontal resolution of
![]() with 10 layers
evenly spaced in log-pressure.
with 10 layers
evenly spaced in log-pressure.
Figures 5-8 show the results of such a simulation. Despite the
motionless initial condition, winds rapidly
develop in response to the day-night heating contrast, reaching
an approximate steady state after ![]() 400 Earth days.
Snapshots at 42 and 466 days are shown in Figs. 5 and 6, respectively.
In these figures, each panel shows pressure on an isentrope
(greyscale) and winds (vectors) for three of the model layers
corresponding to mean pressures of roughly 0.4, 6, and 100 bars
(top to bottom, respectively). The greyscale is such that,
on an isobar, light regions are hot and dark regions are cold.
400 Earth days.
Snapshots at 42 and 466 days are shown in Figs. 5 and 6, respectively.
In these figures, each panel shows pressure on an isentrope
(greyscale) and winds (vectors) for three of the model layers
corresponding to mean pressures of roughly 0.4, 6, and 100 bars
(top to bottom, respectively). The greyscale is such that,
on an isobar, light regions are hot and dark regions are cold.
![\begin{figure}
\par\resizebox{10.8cm}{!}{\includegraphics[clip]{ms1885f7.ps}}\end{figure}](/articles/aa/full/2002/13/aa1885/Timg163.gif) |
Figure 7:
Additional simulation results at 466 days. Arrows are identical
to those in Fig. 6, but here greyscale is vertical velocity
|
The simulation exhibits several interesting features.
First, peak winds exceed 1 km s-1, but despite these
winds, a horizontal temperature contrast is maintained.
The dayside (longitudes
![]() to
to
![]() )
is on average hotter than the nightside, but
dynamics distorts the temperature pattern in a
complicated manner. Second, an equatorial jet
develops that contains most of the kinetic energy.
The jet initially exhibits both eastward and westward
branches (Fig. 5) but eventually becomes only eastward
(Fig. 6), and extends from
)
is on average hotter than the nightside, but
dynamics distorts the temperature pattern in a
complicated manner. Second, an equatorial jet
develops that contains most of the kinetic energy.
The jet initially exhibits both eastward and westward
branches (Fig. 5) but eventually becomes only eastward
(Fig. 6), and extends from
![]() to
to
![]() in latitude. Third, away from the equator, winds
develop that tend to skirt parallel to the temperature
contours. This is an indication that geostrophic balance
holds. (Because the thermal structure is independent of
height to zeroeth order and we have assumed no deep barotropic
flow, horizontal pressure and
temperature gradients are parallel.) Nevertheless, winds
are able to cross isotherms near the equator, and this is
important in setting the day-night temperature contrast.
As expected from the order-of-magnitude arguments in Sect. 4.1,
the jets and gyres that exist are broad in scale,
with a characteristic width of the planetary radius.
in latitude. Third, away from the equator, winds
develop that tend to skirt parallel to the temperature
contours. This is an indication that geostrophic balance
holds. (Because the thermal structure is independent of
height to zeroeth order and we have assumed no deep barotropic
flow, horizontal pressure and
temperature gradients are parallel.) Nevertheless, winds
are able to cross isotherms near the equator, and this is
important in setting the day-night temperature contrast.
As expected from the order-of-magnitude arguments in Sect. 4.1,
the jets and gyres that exist are broad in scale,
with a characteristic width of the planetary radius.
In the simulation,
the day-night temperature difference (measured on isobars)
is about ![]() .
This value depends on the adopted heating rate,
which was chosen to be appropriate to the region where the
pressure is tens of bars. Simulations
that accurately predict the day-night temperature difference
at 1 bar will require a more realistic heating-rate scheme;
we will present such simulations in a future paper.
.
This value depends on the adopted heating rate,
which was chosen to be appropriate to the region where the
pressure is tens of bars. Simulations
that accurately predict the day-night temperature difference
at 1 bar will require a more realistic heating-rate scheme;
we will present such simulations in a future paper.
The temperature patterns in Figs. 5 and 6 show
that Earth-based infrared measurements can shed light
on the circulation of Pegasi planets. In Fig. 6,
the superrotating equatorial jet blows the high-temperature region
downwind. The highest-temperature region is thus
not at the substellar point but lies eastward
by about
![]() in longitude. The maximum
and minimum temperatures would thus face Earth
before the transit of the planet behind
and in front of the star, respectively. On the
other hand, if a broad westward jet existed instead,
the maximum and minimum temperatures would face Earth
after the transits. Therefore, an infrared
lightcurve of the planet throughout its orbital cycle
would help determine the direction and strength of
the atmospheric winds.
in longitude. The maximum
and minimum temperatures would thus face Earth
before the transit of the planet behind
and in front of the star, respectively. On the
other hand, if a broad westward jet existed instead,
the maximum and minimum temperatures would face Earth
after the transits. Therefore, an infrared
lightcurve of the planet throughout its orbital cycle
would help determine the direction and strength of
the atmospheric winds.
In the simulation, the intense heating and cooling causes air to change entropy and leads to vertical motion, as shown in Fig. 7. Light regions (Fig. 7) indicate heating, which causes ascent, and dark regions indicate cooling, which causes descent. Air is thus exchanged between model layers. This exchange also occurs across the model's lowermost isentrope, which separates the radiative layer from the convective interior (Fig. 7, bottom). Because upgoing and downgoing air generally have different kinetic energies and momenta, energy and momentum can thus be exchanged between the atmosphere and interior.
Figure 8 indicates how the steady state is achieved.
The build-up of the mass-weighted mean speed (top panel)
involves two timescales. Over the first 10 days,
the mean winds accelerate to
![]() ,
and the peak speeds approach 1 km s-1.
This is the timescale for pressure gradients to accelerate
the winds and force balances to be established. The flow then
undergoes an additional, slower (
,
and the peak speeds approach 1 km s-1.
This is the timescale for pressure gradients to accelerate
the winds and force balances to be established. The flow then
undergoes an additional, slower (![]() 300 day) increase in
mean speed to
300 day) increase in
mean speed to
![]() ,
with peak speeds of
,
with peak speeds of
![]() 1.5 km s-1. This timescale is that for exchange
of momentum with the interior, across the model's lowermost
isentrope, to reach steady state, as shown in Fig. 8, middle.
1.5 km s-1. This timescale is that for exchange
of momentum with the interior, across the model's lowermost
isentrope, to reach steady state, as shown in Fig. 8, middle.
![\begin{figure}
\par\resizebox{\hsize}{!}{\hspace{0.8cm}\includegraphics[angle=0]{ms1885f8.ps}}\par\end{figure}](/articles/aa/full/2002/13/aa1885/Timg172.gif) |
Figure 8:
Top: mass-weighted mean wind speed within the model domain
( |
In the simulation, kinetic energy is transported from the
atmosphere into the interior at a rate that reaches
![]() (Fig. 8, bottom). This downward transport of kinetic energy
is
(Fig. 8, bottom). This downward transport of kinetic energy
is ![]() 1% of the absorbed stellar flux and
is great enough to affect the radius of HD 209458b,
as shown in Paper I. Although the simulation described here
does not determine the kinetic energy's fate once it reaches
the convective interior, we expect that
tidal friction, Kelvin-Helmholtz instabilities, or other
processes could convert these winds to thermal energy. The exact
kinetic energy flux will depend on whether a deep barotropic
flow exists. Furthermore, potential and thermal energy are also transported
through the boundary, and pressure work is done across it.
Our aim here
is not to present detailed diagnostics of the energetics,
but simply to point out that energy fluxes that are large enough to
be important can occur. We are currently conducting more detailed
simulations to determine the sensitivity of the simulations
to a deep barotropic flow, and we will present the
detailed energetics of these simulations in a future paper.
1% of the absorbed stellar flux and
is great enough to affect the radius of HD 209458b,
as shown in Paper I. Although the simulation described here
does not determine the kinetic energy's fate once it reaches
the convective interior, we expect that
tidal friction, Kelvin-Helmholtz instabilities, or other
processes could convert these winds to thermal energy. The exact
kinetic energy flux will depend on whether a deep barotropic
flow exists. Furthermore, potential and thermal energy are also transported
through the boundary, and pressure work is done across it.
Our aim here
is not to present detailed diagnostics of the energetics,
but simply to point out that energy fluxes that are large enough to
be important can occur. We are currently conducting more detailed
simulations to determine the sensitivity of the simulations
to a deep barotropic flow, and we will present the
detailed energetics of these simulations in a future paper.
The evolution of angular momentum (Fig. 8, middle) helps explain why the circulation changes from Figs. 5 to 6. After 42 days (Fig. 5), eastward midlatitude winds have already developed that balance the negative equator-to-pole temperature gradient. But at this time, the atmosphere's angular momentum is still nearly zero relative to the synchronously-rotating state, so angular momentum balance requires westward winds along some parts of the equator. (Interestingly, in these regions, the temperature increases with latitude, as expected from geostrophy.) The circulation involves upwelling on the dayside and equatorial flow - both east and west - to the nightside, where downwelling occurs. This circulation is similar in some respects to the Walker circulation in Earth's atmosphere. After 466 days, however, the atmosphere has gained enough angular momentum that the equatorial jet is fully superrotating. Some westward winds exist at high latitudes, but they are weak enough that the net angular momentum is still eastward.
Application of the arguments from Sect. 4.2
provides a consistency check.
The mean heating rate in the simulations is about
![]() .
Inserting this value
into Eqs. (16)-(17), we obtain
.
Inserting this value
into Eqs. (16)-(17), we obtain
![]() and
and
![]() .
These compare well with
the day-night temperature difference and mass-weighted
mean speed of
.
These compare well with
the day-night temperature difference and mass-weighted
mean speed of ![]() and
and
![]() that are obtained
in the simulation. (For the estimate, we used
that are obtained
in the simulation. (For the estimate, we used
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .) If Eqs. (20)-(21) are adopted instead,
using values of
.) If Eqs. (20)-(21) are adopted instead,
using values of
![]() and H=300 km, we
obtain temperature differences and speeds of
and H=300 km, we
obtain temperature differences and speeds of ![]() and
and
![]() .
Compared to the simulation, these estimates
are too high by a factor of
.
Compared to the simulation, these estimates
are too high by a factor of ![]() 2, but are still of the
correct order of magnitude. An important point is that
the maximum speed in the simulation substantially
exceeds that from the simple estimates; the estimates are
most relevant for the mean speed.
2, but are still of the
correct order of magnitude. An important point is that
the maximum speed in the simulation substantially
exceeds that from the simple estimates; the estimates are
most relevant for the mean speed.
As shown in the appendix, hot and cold regions on the planet may have distinct chemical equilibrium compositions. Advection of air between these regions plays a key role for the (disequilibrium) chemistry in the atmosphere. Cloud formation critically depends on whether vertical motions dominate over horizontal motions. This in turns affects the albedo and depth to which stellar light is absorbed.
Clouds form when the temperature of moving air parcels decreases enough for the vapor pressure of condensible vapors to become supersaturated. If dayside heating and nightside cooling are balanced only by horizontal advection, air flowing from dayside to nightside remains at constant pressure but decreases in temperature (hence entropy) because of the radiative cooling. Nightside condensation may occur, and particle fallout limits the total mass of the trace constituent (vapor plus condensates) in this air. As the air flows onto the dayside, its temperature increases and any existing clouds will sublimate. This scenario therefore implies that the dayside will be cloud-free.
In an alternate scenario, dayside heating and nightside cooling are balanced by vertical advection, at least near the sub- and antisolar points. Because entropy increases with altitude in a stably-stratified atmosphere, this scenario implies that ascent occurs on the dayside and descent on the nightside. Clouds may therefore form on the dayside, increasing the albedo and decreasing the pressure at which stellar light is absorbed.
In reality, both horizontal and vertical advection are important, and the real issue is to determine the relative contribution. We are pursuing more detailed numerical simulations to address this issue.
Copyright ESO 2002