It has been shown that the tides raised by the star on Pegasi planets![]() should rapidly drive them into synchronous rotation (Guillot et al. 1996; Marcy et al. 1997; Lubow et al. 1997). This can be seen by considering the
time scale to tidally despin the planet (Goldreich & Soter
1966; Hubbard 1984):
should rapidly drive them into synchronous rotation (Guillot et al. 1996; Marcy et al. 1997; Lubow et al. 1997). This can be seen by considering the
time scale to tidally despin the planet (Goldreich & Soter
1966; Hubbard 1984):
Nevertheless, stellar heating drives the atmosphere away from synchronous rotation, raising the possibility that the interior's rotation state is not fully synchronous. Here, we discuss (1) the energies associated with the planet's initial transient spindown, and (2) the possible equilibrium states that could exist at present.
Angular momentum conservation requires that as the planet spins down, the orbit
expands. The energy dissipated during the spindown process is the
difference between
the loss in spin kinetic energy and the gain in orbital energy:
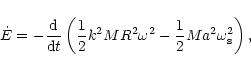 |
(2) |
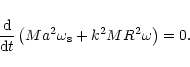 |
(3) |
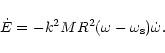 |
(4) |
The total energy dissipated is
![]() ,
neglecting variation of the orbital
distance. Using the moment of inertia and rotation rate of
Jupiter (k2=0.26 and
,
neglecting variation of the orbital
distance. Using the moment of inertia and rotation rate of
Jupiter (k2=0.26 and
![]() ), we
obtain for HD 209458b
), we
obtain for HD 209458b
![]() .
If
this energy were dissipated evenly throughout the planet,
it would imply a global temperature increase of 1400K.
.
If
this energy were dissipated evenly throughout the planet,
it would imply a global temperature increase of 1400K.
By definition of the synchronization timescale, the dissipation rate
can be written:
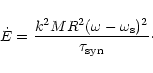 |
(5) |
The thermal pulse associated with the initial spindown is large
enough that, if the energy is dissipated in the planet's interior,
it may affect the planet's radius. It has previously been argued
(Burrows et al. 2000) that Pegasi planets![]() must have migrated
inward during their first 107years of evolution; otherwise, they
would have contracted too much to explain
the observed radius of HD 209458b. But the thermal pulse associated
with spindown was not included in the calculation, and this extra
energy source may extend the time over which migration was possible.
Nevertheless, it seems difficult to invoke tidal synchronization
as the missing heat source necessary to explain HD 209458b's present (large)
radius. High dissipation rates are possible if
must have migrated
inward during their first 107years of evolution; otherwise, they
would have contracted too much to explain
the observed radius of HD 209458b. But the thermal pulse associated
with spindown was not included in the calculation, and this extra
energy source may extend the time over which migration was possible.
Nevertheless, it seems difficult to invoke tidal synchronization
as the missing heat source necessary to explain HD 209458b's present (large)
radius. High dissipation rates are possible if
![]() is small, but
in the absence of a mechanism to prevent synchronization,
is small, but
in the absence of a mechanism to prevent synchronization,
![]() would drop as soon as
would drop as soon as
![]() .
The most efficient way of
slowing the planet's contraction is then to invoke
.
The most efficient way of
slowing the planet's contraction is then to invoke
![]() years. In that case, the energy dissipated
becomes
years. In that case, the energy dissipated
becomes
![]() ,
which is two orders of
magnitude smaller than that necessary to significantly affect the
planet's evolution (Paper I; Bodenheimer et al. 2001). For the
present-day dissipation to be significant, an initial
rotation rate 10 times that of modern-day Jupiter would be needed.
But the centripetal acceleration due to rotation exceeds the
gravitational acceleration at the planet's surface for rotation
rates only twice that of modern-day Jupiter, so this possibility is
ruled out. Furthermore, such long spindown times
would require a tidal Q of
,
which is two orders of
magnitude smaller than that necessary to significantly affect the
planet's evolution (Paper I; Bodenheimer et al. 2001). For the
present-day dissipation to be significant, an initial
rotation rate 10 times that of modern-day Jupiter would be needed.
But the centripetal acceleration due to rotation exceeds the
gravitational acceleration at the planet's surface for rotation
rates only twice that of modern-day Jupiter, so this possibility is
ruled out. Furthermore, such long spindown times
would require a tidal Q of ![]() 109-1010,
which is
109-1010,
which is ![]() 104 times the Q values inferred for Jupiter,
Uranus, and Neptune from constraints on their satellites' orbits
(Peale 1999; Banfield & Murray 1992; Tittemore &
Wisdom 1989).
Dissipation of the energy due to transient loss
of the planet's initial spin energy therefore cannot provide the
energy needed to explain the radius of HD 209458b.
104 times the Q values inferred for Jupiter,
Uranus, and Neptune from constraints on their satellites' orbits
(Peale 1999; Banfield & Murray 1992; Tittemore &
Wisdom 1989).
Dissipation of the energy due to transient loss
of the planet's initial spin energy therefore cannot provide the
energy needed to explain the radius of HD 209458b.
Another possible source of energy is through circularization of the
orbit. Bodenheimer et al. (2001) show that the resulting
energy dissipation could reach
![]() if the planet's
tidal Q is 106 and if a hypothetical companion planet pumps HD 209458b's
eccentricity to values near its current observational upper limit of 0.04.
If such a companion is absent, however, the orbital circularization time is
if the planet's
tidal Q is 106 and if a hypothetical companion planet pumps HD 209458b's
eccentricity to values near its current observational upper limit of 0.04.
If such a companion is absent, however, the orbital circularization time is
![]() 108 years, so this source of heating would be negligible at present.
Longer circularization times of
109-1010 years would allow the heating
to occur until the present-day, but its magnitude is then reduced to
108 years, so this source of heating would be negligible at present.
Longer circularization times of
109-1010 years would allow the heating
to occur until the present-day, but its magnitude is then reduced to
![]() or lower, which is an order of magnitude smaller
than the dissipation required.
or lower, which is an order of magnitude smaller
than the dissipation required.
The existence of atmospheric winds implies that the atmosphere is not synchronously rotating. Because dynamics can transport angular momentum vertically and horizontally (including the possibility of downward transport into the interior), the interior may evolve to an equilibrium rotation state that is asynchronous. Here we examine the possibilities.
Let us split the
planet into an "atmosphere'', a part of small mass for which
thermal effects are significant, and an "interior'' encompassing most
of the mass which has minimal horizontal thermal contrasts. Suppose
(since
![]() is short) that the system has reached steady
state. Consider two cases, depending
on the physical mechanisms that
determine the gravitational torque on the atmosphere.
is short) that the system has reached steady
state. Consider two cases, depending
on the physical mechanisms that
determine the gravitational torque on the atmosphere.
The first possibility is that the gravitational torque on the atmosphere
pushes the atmosphere away from synchronous rotation (i.e., it
increases the magnitude of the atmosphere's angular momentum measured
in the synchronously-rotating reference frame)
as has been hypothesized for Venus (Ingersoll & Dobrovolskis
1978; Gold & Soter 1969).
To balance the torque on the atmosphere, the interior
must have a net angular momentum of the same sign as the atmosphere
(so that both either super- or subrotate). In Fig. 3,
superrotation then corresponds to a clockwise flux of angular momentum,
whereas subrotation corresponds to the anticlockwise scenario.
| |
Figure 3:
Angular momentum flow between orbit, interior, and atmosphere
for a Pegasi planet |
The second possibility is that the gravitational torque on the atmosphere
tends to synchronize the atmosphere. This possibility may be relevant
because, on a gas-giant planet, it is unclear that the high-temperature
and high-pressure regions would be ![]() out of phase, as is
expected on a terrestrial planet. If the interior responds
sufficiently to atmospheric perturbations to keep the deep
isobars independent
of surface meteorology (an assumption that seems to work well in modeling
Jupiter's cloud-layer dynamics), then high-pressure and
high-temperature regions will
be in phase, which would sweep the high-mass regions downwind
and lead to a torque
that synchronizes the atmosphere. Furthermore, if a resonance occurs
between the
tidal frequency and the atmosphere's wave-oscillation frequency, the
resulting gravitational
torques also act to synchronize the atmosphere (Lubow et al. 1997).
In this case, the interior and atmosphere have net angular momenta of opposite
signs. Depending on the sign of the atmosphere/interior momentum flux,
this situation would correspond in Fig. 3 to either the
clockwise or anticlockwise circulation of angular momentum cases.
out of phase, as is
expected on a terrestrial planet. If the interior responds
sufficiently to atmospheric perturbations to keep the deep
isobars independent
of surface meteorology (an assumption that seems to work well in modeling
Jupiter's cloud-layer dynamics), then high-pressure and
high-temperature regions will
be in phase, which would sweep the high-mass regions downwind
and lead to a torque
that synchronizes the atmosphere. Furthermore, if a resonance occurs
between the
tidal frequency and the atmosphere's wave-oscillation frequency, the
resulting gravitational
torques also act to synchronize the atmosphere (Lubow et al. 1997).
In this case, the interior and atmosphere have net angular momenta of opposite
signs. Depending on the sign of the atmosphere/interior momentum flux,
this situation would correspond in Fig. 3 to either the
clockwise or anticlockwise circulation of angular momentum cases.
In both cases above, the gravitational torque on the atmosphere arises because of spatial density variations associated with surface meteorology, which are probably confined to pressures less than few hundred bars. Therefore, this torque acts on only a small fraction of the planet's mass. In contrast, the gravitational torque on the gravitational tidal bulge affects a much larger fraction of the planet's mass. It is not necessarily true that the torque on the atmosphere is negligible in comparison with the torque on the interior, however, because the gravitational tidal bulge is only slightly out of phase with the line-of-sight to the star (e.g., the angle is 10-5 radians for Jupiter). In contrast, the angle between the meteorologically-induced density variations and the line of sight to the star could be up to a radian. Detailed calculations of torque magnitudes would be poorly constrained, however, and will be left for the future.
Several mechanisms may act to transfer angular momentum between the atmosphere and interior. Kelvin-Helmholtz shear instabilities, if present, would smooth interior-atmosphere differential rotation. On the other hand, waves transport angular momentum and, because they act nonlocally, often induce differential rotation rather than removing it. The quasi-biennial oscillation on Earth is a classic example (see, e.g., Andrews et al. 1987, Chapter 8). Atmospheric tides (large-scale waves forced by the solar heating) are another example of such a wave; on Venus, tides play a key role in increasing the rotation rate of the cloud-level winds. Finally, vertical advection may cause angular momentum exchange between the atmosphere and the interior of Pegasi planets, because the angular momentum of air in updrafts and downdrafts need not be the same.
A simple estimate illustrates the extent of nonsynchronous rotation
possible in the interior. Suppose that the globally-averaged flux
of absorbed starlight is
![]() ,
which is of order
,
which is of order
![]() for
Pegasi planets
for
Pegasi planets![]() near 0.05 AU, and that the globally-averaged flux of
kinetic energy transported from the atmosphere to the interior
is
near 0.05 AU, and that the globally-averaged flux of
kinetic energy transported from the atmosphere to the interior
is
![]() ,
where
,
where ![]() is small and dimensionless. If this kinetic energy
flux is balanced by dissipation in the interior
with a spindown timescale of
is small and dimensionless. If this kinetic energy
flux is balanced by dissipation in the interior
with a spindown timescale of
![]() ,
then the deviation of
the rotation frequency from synchronous is
,
then the deviation of
the rotation frequency from synchronous is
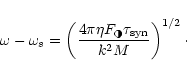 |
(6) |
As discussed in Sect. 4, experience with planets in our solar system
suggests that atmospheric kinetic energy is generated at a
flux of
![]() ,
and if all of this energy enters the
interior, then
,
and if all of this energy enters the
interior, then
![]() .
Using a spindown time of
.
Using a spindown time of
![]() years
implies that
years
implies that
![]() ,
which is comparable to the synchronous rotation frequency. The implied
winds in the interior are then of order
,
which is comparable to the synchronous rotation frequency. The implied
winds in the interior are then of order ![]()
![]() .
Even
if
.
Even
if ![]() is only
10-4, the interior's winds would be
is only
10-4, the interior's winds would be
![]() .
The implication
is that the interior's spin could be asynchronous by up to a factor of two,
depending on the efficiency of energy and momentum transport into the
interior. If spindown times of
.
The implication
is that the interior's spin could be asynchronous by up to a factor of two,
depending on the efficiency of energy and momentum transport into the
interior. If spindown times of ![]() 106 years turn out to be
serious under- or overestimates, then greater or lesser asynchronous
rotation would occur, respectively.
106 years turn out to be
serious under- or overestimates, then greater or lesser asynchronous
rotation would occur, respectively.
Copyright ESO 2002