5 Appendix - Good or bad approximations?

Several simplifications were done in the above calculations. It is thus important to confirm that they are justified.

5.1 Solar mass loss

Including both electromagnetic radiation and particle radiation the relative solar mass loss is: $({\rm d}M_{\rm s}/{\rm d}t)/M_{\rm s}=-9.13\times 10^{-14}~\rm yr^{-1}$ (Noerdlinger 2001). In our mass units, the mass of the Sun is $2.9591221 \times 10^{-4}$. The total mass loss in 1 Myr is then about $2.7\times 10^{-11}$ while the estimated accuracy of the solar mass is of the same order. It is thus unlikely that solar mass loss would give any significant change in the results of present work (cf. Quinn et al. 1991).

5.2 Tides

Present tides result in an expansion of the Moon orbit of 3.82 cm/yr (Dickey et al. 1994) or 38.2 km/Myr or 0.01 percent of the Earth-Moon distance which is very small compared to other variations in the Moon orbit. There is also an expected decrease of Earth's spin angular velocity for the future.

Laskar et al. (1993b) performed simulations both with and without tides [(CMAR, FGAM) = (1, 1) and (0, 1) respectively, see program La93 of Laskar et al. (1993c)]. It can there be observed that the maximum difference in obliquity up to 1 Myr before present is less than 0.04$^{\circ }$. By comparing the solutions it is obvious that the inclusion of tides results in a small phase difference only (it is less than a few 100 years). For simulations longer than a few Myr, it is necessary to include tides. Fortunate for present work, the tidal effects are so tiny for 1-2 Myr simulations that they can hardly be detected by the eye and can thus be disregarded. Moreover, Laskar et al. (1993b) argued that Earth's moments of inertia (and tidal dissipation) may change considerably during glaciation giving quite different solutions for simulations earlier than about 2-3 Myr (see their Fig. 10). If these uncertainties are real, it is actually questionable if realistic long simulations are at all possible.

5.3 Effects of general relativity

General relativity (GR) effects can be studied by adding a correction to the usual equation of motion in a heliocentric system. The correction for particle i may be found in the DE102 ephemeris article of Newhall et al. (1983) or Quinn et al. (1991):

$$\frac{GM_{\rm s}}{r^{3}_{i}}\overline{r}_{i}\left( 2\left( \b... ...ine{v}_{i}\left( \overline{r}_{i}\cdot \overline{v}_{i}\right)$$ (35)

where GR corresponds to the PPN parameters $\beta _{\rm ppn}=\gamma _{\rm ppn}=1$. Relativistic effects are quite important for Mercury. The well known relativistic contribution to the orbital precession rate is about 43 $^{\prime\prime}$/century as compared to the classical value of about 532 $^{\prime\prime}$/century from many particle interactions. However, Mercury is affecting Earth's spin axis very little due to the distance and low mass of Mercury. This effect is therefore expected to be negligible. It is nevertheless very interesting to study this further. Figure 18 shows the evolution of the mean precession rates 100 kyr back in time for both the GR and classical approach. These precession rates are derived from angles sampled at 1 kyr intervals (see Sect. 2.9). It is interesting to note that the variations are quite large. The figure indicates that the present 1 kyr means are around 532 (classical) and 575 (GR) arcsec/cy in agreement with the generally accepted values. The difference between the curves results in the inset figure. Although the present isolated GR effect is 43 arcsec/cy, it is quite interesting to realise that the values vary quite considerably. About 100000 years ago the correct value was instead 33 arcsec/cy.

Figure 18: Orbital precession rates of Mercury displayed as 1 kyr means during the last 100 kyr. The x-curve is due to a pure classical simulation while the o-curve corresponds to corrections from GR. The inset figure displays the isolated GR effect (i.e. the difference between o- and x-curve).

For Mercury, Venus, Earth, Mars and Jupiter the 1000 yr mean perihelion advancements due to general relativity are found to be 42.91, 8.36, 4.08, 1.35 and 0.054 $^{\prime\prime}$/century, respectively. This was also computed by first performing a classical 1000 yr long simulation and then compare it with a similar simulation with the GR-correction included. Although the influence is quite small, it is even less important since the orbits of Venus and Earth are nearly circular (the velocity term becomes negligible). Experimentally it is certainly also extremely difficult to measure. Further, for the acceleration of the Earth-Moon system it is according to Quinn et al. [p. 2287] about an order of magnitude more important to consider the quadrupole moment of the Earth-Moon system correctly than to include general relativity effects. This quadrupole moment is fully accounted for in present approach. For the time span we are primarily interested in ($\sim$1 Myr), relativistic effects should be comparatively small. Nevertheless, it is interesting to perform a few simulations with GR included to verify that the above assumption is correct.

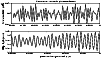Figure 19: Earth summer radiation and obliquity using our classical and GR treatment. The differences are clearly small and can hardly be detected.

Summer radiation and obliquity are important climatic variables for this purpose. Figure 19 displays these quantities for both the classical and the GR simulations. In practise they are very similar. In the case for the summer radiation power, there are actually some slight deviations starting to develop at 350 kyr before present, but they are so tiny that it is difficult to detect by the eye. We can thus conclude that the approximations are reasonably good up to about 1 Myr or so for climatic purposes of the Earth. In the case of the Mars calculations, GR is much less important and the effect is negligible for simulations of several Myr. Interested parties may investigate these intricate differences further by obtaining our converged files of the 2 Myr simulations for both cases: the classical and the GR approach [http://www.fmi.mh.se/celmech].