A&A 383, 747-754 (2002)
DOI: 10.1051/0004-6361:20011812
T.-S. Kim1 - S. Cristiani2,3 - S. D'Odorico1
1 - European Southern Observatory,
Karl-Schwarzschild-Strasse 2, 85748 Garching b.
München, Germany
2 -
ST European Coordinating Facility, ESO,
Karl-Schwarzschild-Strasse 2, 85748 Garching b.
München, Germany
3 -
Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11,
34131 Trieste, Italy
Received 25 August 2001 / Accepted 14 December 2001
Abstract
Using a new, increased dataset of 7 QSOs from VLT/UVES observations combined
with one QSO from the literature,
the minimum Doppler parameters as a function of neutral hydrogen
column density
![]() ,
,
![]() ,
of the Ly
,
of the Ly![]() forest
has been derived at three redshifts
forest
has been derived at three redshifts ![]() 2.1, 3.3 and 3.8.
In particular, five QSOs at
2.1, 3.3 and 3.8.
In particular, five QSOs at ![]() 2.1 enable us to study the
cosmic variance of
2.1 enable us to study the
cosmic variance of
![]() at
lower z for the first time.
When incompleteness of the number of the observed lines towards
lower
at
lower z for the first time.
When incompleteness of the number of the observed lines towards
lower
![]() is accounted for, the derived
slopes of
is accounted for, the derived
slopes of
![]() ,
,
![]() ,
are consistent
with no-z evolution with an indication of lower value at
,
are consistent
with no-z evolution with an indication of lower value at
![]() 3.3,
while
3.3,
while
![]() at a fixed column density
at a fixed column density
![]() ,
,
![]() ,
increases as z decreases. Assuming a QSO-dominated UV background,
the slope of the equation of state
,
increases as z decreases. Assuming a QSO-dominated UV background,
the slope of the equation of state
![]() shows no
z-evolution within large uncertainties and
the temperature at the mean density, T0, decreases
as z decreases at three redshift ranges.
There is a large fluctuation of
shows no
z-evolution within large uncertainties and
the temperature at the mean density, T0, decreases
as z decreases at three redshift ranges.
There is a large fluctuation of
![]() and
and
![]() even at the similar
redshifts, in particular at
even at the similar
redshifts, in particular at ![]() 3.3 and 3.8.
The lower
3.3 and 3.8.
The lower
![]() and higher
and higher
![]() values at
values at
![]() and 3.6 compared to ones at
and 3.6 compared to ones at
![]() and 3.9
are caused by a lack of lower-
and 3.9
are caused by a lack of lower-
![]() and lower-blines at lower-z parts of each QSO at z > 3, probably due to
the He II reionization.
This result suggests that an impact from the He II
reionization on the forest might be mainly on the lower-
and lower-blines at lower-z parts of each QSO at z > 3, probably due to
the He II reionization.
This result suggests that an impact from the He II
reionization on the forest might be mainly on the lower-
![]() forest. From this new dataset, we find some forest clouds with
a high ratio of Si IV column density to C IV column
density,
forest. From this new dataset, we find some forest clouds with
a high ratio of Si IV column density to C IV column
density,
![]() /
/
![]() ,
at z < 2.5, although the bulk of
the forest clouds shows lower
,
at z < 2.5, although the bulk of
the forest clouds shows lower
![]() /
/
![]() .
This high
.
This high
![]() /
/
![]() at z < 2.5 suggests that some forest
clouds are exposed to a soft UV background.
This lack of strong discontinuity of
at z < 2.5 suggests that some forest
clouds are exposed to a soft UV background.
This lack of strong discontinuity of
![]() /
/
![]() at
at
![]() at
at ![]() suggests that
suggests that
![]() /
/
![]() might not be a good observational tool to probe the He II
reionization and/or that the UV background might be
strongly affected by local, high-z galaxies at z < 3.
might not be a good observational tool to probe the He II
reionization and/or that the UV background might be
strongly affected by local, high-z galaxies at z < 3.
Key words: cosmology: observations - quasars: general - intergalactic medium
The Ly![]() forest imprinted in the spectra of
high-z QSOs
arises from the fluctuating low-density intergalactic
medium (IGM), highly photoionized by the metagalactic UV background.
Since the universe expands adiabatically and the Ly
forest imprinted in the spectra of
high-z QSOs
arises from the fluctuating low-density intergalactic
medium (IGM), highly photoionized by the metagalactic UV background.
Since the universe expands adiabatically and the Ly![]() forest
is in photoionization equilibrium with the UV background,
the temperature of the Ly
forest
is in photoionization equilibrium with the UV background,
the temperature of the Ly![]() forest as a function of z
provides a unique and powerful tool to probe the physical
state of the IGM and the reionization history of the universe
(Hui & Gnedin 1997;
Schaye et al. 1999; Ricotti, Gnedin & Shull 2000;
McDonald et al. 2000).
forest as a function of z
provides a unique and powerful tool to probe the physical
state of the IGM and the reionization history of the universe
(Hui & Gnedin 1997;
Schaye et al. 1999; Ricotti, Gnedin & Shull 2000;
McDonald et al. 2000).
For a low-density (the baryon overdensity
![]()
![]() 10),
photoionized gas, the temperature of the gas is shown to be
tightly correlated with the overdensity of the gas.
This relation, i.e. the equation of state, is defined by
10),
photoionized gas, the temperature of the gas is shown to be
tightly correlated with the overdensity of the gas.
This relation, i.e. the equation of state, is defined by
![]() ,
where T is
the gas temperature
in K, T0 is the gas temperature in K
at the mean gas density and
,
where T is
the gas temperature
in K, T0 is the gas temperature in K
at the mean gas density and
![]() is a constant at a given
redshift z. Both T0 and
is a constant at a given
redshift z. Both T0 and
![]() are a function
of z, depending on the thermal history of the IGM
(Hui & Gnedin 1997).
are a function
of z, depending on the thermal history of the IGM
(Hui & Gnedin 1997).
This equation of state, however, is not directly observable.
Instead of T and
![]() ,
observations only provide
the neutral hydrogen column density
,
observations only provide
the neutral hydrogen column density
![]() (in
cm-2) and the Doppler parameter b (in km s-1)
of the forest absorption lines. In practice, a lower cutoff envelope
in the
(in
cm-2) and the Doppler parameter b (in km s-1)
of the forest absorption lines. In practice, a lower cutoff envelope
in the
![]() -b distribution is used to probe
the upper limit on the temperature of the IGM since the forest
lines could be broadened by processes other than the thermal
broadening. Translating a
-b distribution is used to probe
the upper limit on the temperature of the IGM since the forest
lines could be broadened by processes other than the thermal
broadening. Translating a
![]() -b envelope into
a
-b envelope into
a
![]() -T relation depends on many physical
assumptions, such as the ionizing UV background
-T relation depends on many physical
assumptions, such as the ionizing UV background ![]() (Miralda-Escudé et al. 1996; Schaye et al.
1999).
(Miralda-Escudé et al. 1996; Schaye et al.
1999).
This minimum Doppler cutoff
![]() can be described by
can be described by
| QSO |
|
mag
|
|
|
# of lines
|
Comments |
| Q1101-264 | 2.145 | 16.0 | 3500-3778 | 1.88-2.11 | 69 | UVES SV, a damped system at z=1.8386 |
| J2233-606 | 2.238 | 17.5 | 3500-3890 | 1.88-2.20 | 88 | UVES Commissioning I |
| HE1122-1648 | 2.400 | 17.7 | 3500-4091 | 1.88-2.37 | 179 | UVES SV, split into 2 |
| HE2217-2818 | 2.413 | 16.0 | 3510-4100 | 1.89-2.37 | 159 | UVES Commissioning I, split into 2 |
| HE1347-2457 | 2.534 | 16.8 | 3760-4100 | 2.09-2.37 | 91 | UVES SV, incomplete observations |
| Q0302-003 | 3.281 | 18.4 | 4808-5150 | 2.96-3.24 | 107 | UVES Commissioning I, incomplete observations |
| Q0055-269 | 3.655 | 17.9 | 4850-5598 | 2.99-3.60 | 264 | UVES, Sep. 20-22, 2000, split into 2 |
| Q0000-263 | 4.127 | 17.9 | 5450-6100 | 3.48-4.02 | 209 | Lu et al. (1996), split into 2 |
|
|
From observations alone,
both no z-evolution of
![]() -independent
-independent ![]() (Kirkman & Tytler 1997; Savaglio et al. 1999) and
increasing
(Kirkman & Tytler 1997; Savaglio et al. 1999) and
increasing ![]() with decreasing z (Kim et al. 1997)
have been claimed. Results from simulations combined with observations
have also claimed both no-z evolution of T0 and
with decreasing z (Kim et al. 1997)
have been claimed. Results from simulations combined with observations
have also claimed both no-z evolution of T0 and
![]() (McDonald et al. 2000)
and a z-evolution
(Ricotti et al. 2000; Schaye et al. 2000;
Kim et al.
2001a).
Deriving
(McDonald et al. 2000)
and a z-evolution
(Ricotti et al. 2000; Schaye et al. 2000;
Kim et al.
2001a).
Deriving
![]() from observations depends
on many factors such as
the method of line deblending, the number of available
absorption lines, the metal-line contamination, and the method of fitting
the lower
from observations depends
on many factors such as
the method of line deblending, the number of available
absorption lines, the metal-line contamination, and the method of fitting
the lower
![]() -b envelope (Hu et al.
1995; Kirkman & Tytler 1997; Bryan & Machacek
2000; McDonald et al. 2000; Ricotti et al. 2000;
Shaye et al. 2000; Kim et al. 2001a).
The different approaches and the limited numbers of lines have led, in
part,
to the contradicting
results on the evolution of
-b envelope (Hu et al.
1995; Kirkman & Tytler 1997; Bryan & Machacek
2000; McDonald et al. 2000; Ricotti et al. 2000;
Shaye et al. 2000; Kim et al. 2001a).
The different approaches and the limited numbers of lines have led, in
part,
to the contradicting
results on the evolution of
![]() in the
literature.
in the
literature.
Here, using a new, increased dataset from 7 QSOs observed with the
VLT/UVES combined with
the published data on one QSO obtained with Keck/HIRES, we present
the evolution of the Doppler cutoff
![]() at three redshifts
at three redshifts
![]() 2.1, 3.3 and 3.8.
In particular, five QSOs at
2.1, 3.3 and 3.8.
In particular, five QSOs at ![]() 2.1 enable us to study the cosmic
variance of
2.1 enable us to study the cosmic
variance of
![]() and to improve
a determination of
and to improve
a determination of
![]() at lower z for the first time.
In Sect. 2, we briefly describe the data used in this study. The
analyses of the observations are presented in Sect. 3.
The discussion is in Sect. 4 and the conclusions are summarized in Sect. 5.
In this study, all the quoted uncertainties are
at lower z for the first time.
In Sect. 2, we briefly describe the data used in this study. The
analyses of the observations are presented in Sect. 3.
The discussion is in Sect. 4 and the conclusions are summarized in Sect. 5.
In this study, all the quoted uncertainties are ![]() errors.
errors.
| Sample A | ||||||||
| <z> |
|
# of lines |
|
|
|
|
|
|
| 2.1 | 13.0-14.5 | 349 |
|
|
|
|
|
|
| 3.3 | 13.0-14.5 | 275 |
|
|
|
|
|
|
| 3.8 | 13.3-14.5 | 152 |
|
|
|
|
|
|
| 2.0 |
13.0-14.5 | 176 |
|
|
|
|
|
|
| 2.2 |
13.0-14.5 | 173 |
|
|
|
|
|
|
| 3.1 |
13.0-14.5 | 157 |
|
|
|
|
|
|
| 3.4 |
13.0-14.5 | 118 |
|
|
|
|
|
|
| 3.6 |
13.3-14.5 | 74 |
|
|
|
|
|
|
| 3.9 |
13.3-14.5 | 78 |
|
|
|
|
|
|
| Sample B (averaged for the individual members) | ||||||||
| 2.1 | 13.0-14.5 | ... |
|
|
|
|
|
|
3.3 |
13.0-14.5 | ... |
|
|
|
|
|
|
3.8 |
13.3-14.5 | ... |
|
|
|
|
|
|
| Results from Schaye et al. (2000) (their sample corresponds to our Sample B) | ||||||||
|
|
12.5-14.5 | ... | ... | ... | ... | ... | ||
| 12.5-14.5 | ... | ... | ... | ... | ... | |||
| 12.5-14.8 | ... | ... | ... | ... | ... | |||
|
|
Table 1 lists the eight QSOs analyzed in this paper.
Seven QSOs were observed with
the UVES spectrograph at the VLT Kueyen telescope (built by
ESO, P.I. S. D'Odorico). The UVES data were
reduced with the MIDAS ECHELLE/UVES package.
The final reduced vacuum heliocentric spectra
have S/N of 30-50 per pixel in the regions of interest and a resolution
of
![]() .
The spectra were normalized locally using a 5th order polynomial
fit. The normalized spectra were then fitted with Voigt profiles
using VPFIT (Carswell et al.:
http://www.ast.cam.ac.uk/~rfc/vpfit.html) with the
reduced
.
The spectra were normalized locally using a 5th order polynomial
fit. The normalized spectra were then fitted with Voigt profiles
using VPFIT (Carswell et al.:
http://www.ast.cam.ac.uk/~rfc/vpfit.html) with the
reduced ![]() threshold of 1.3 to obtain the
three line parameters, z, b and
threshold of 1.3 to obtain the
three line parameters, z, b and
![]() .
The metal lines were
identified and removed as described
in Kim et al. (2001a).
Details of the observations and data reduction, and the
fitted line lists may be found
in Kim et al. (2001a, 2001b).
.
The metal lines were
identified and removed as described
in Kim et al. (2001a).
Details of the observations and data reduction, and the
fitted line lists may be found
in Kim et al. (2001a, 2001b).
The line parameters of Q0000-263
were taken from Lu et al. (1996) to include the highest
redshift Ly![]() forest available in the literature,
with similar resolution and S/N to the UVES data. Their
analysis of Q0000-263 was also undertaken
with VPFIT.
forest available in the literature,
with similar resolution and S/N to the UVES data. Their
analysis of Q0000-263 was also undertaken
with VPFIT.
In order to avoid confusion with the Ly![]() forest
and the proximity effect, we consider only the wavelength range from
the Ly
forest
and the proximity effect, we consider only the wavelength range from
the Ly![]() emission to 3000 km s-1 shortward of
the Ly
emission to 3000 km s-1 shortward of
the Ly![]() emission.
However, the redshift intervals actually used are further
limited by other factors such as the incomplete coverage of the forest
region, a damped Ly
emission.
However, the redshift intervals actually used are further
limited by other factors such as the incomplete coverage of the forest
region, a damped Ly![]() system and
our attempt to overlap the
wavelengths of each QSO as much as possible to
study the cosmic variance of
system and
our attempt to overlap the
wavelengths of each QSO as much as possible to
study the cosmic variance of
![]() .
Table 1 lists the
wavelength ranges used for each QSO.
.
Table 1 lists the
wavelength ranges used for each QSO.
We restrict our analysis to
![]() .
The lower limit corresponds to the detection
threshold in the regions of poorest S/N and the upper limit
is where the
.
The lower limit corresponds to the detection
threshold in the regions of poorest S/N and the upper limit
is where the
![]() estimate from fitting Ly
estimate from fitting Ly![]() alone becomes unreliable because of line saturation. Because
lines in blends can also have large uncertainties, we have
further restricted the analysis to include only those lines
with profile fitting errors less than 25% in
alone becomes unreliable because of line saturation. Because
lines in blends can also have large uncertainties, we have
further restricted the analysis to include only those lines
with profile fitting errors less than 25% in
![]() and b to better define the lower cutoff envelopes
(Schaye et al. 2000; Kim et al. 2001a).
and b to better define the lower cutoff envelopes
(Schaye et al. 2000; Kim et al. 2001a).
In this study, Sample A defines
all the lines available from all QSOs which have treated as a single dataset
at each z. We also define Sample B in order to study a fluctuation
of the Doppler cutoff at similar redshifts. The spectral coverage for
each QSO from the same z bin is not uniform. For those QSOs with
more than ![]() 600 Å coverage
(HE1122-1648, HE2217-2818, Q0055-269
and Q0000-263), the line lists have been divided into
two subsets: a group at higher redshifts and a group at lower redshifts. The rest
of the QSOs do not have enough coverage to make this splitting possible
and provide only one group each. We label the ensemble of these
groups Sample B.
Each group of Sample B
spans 300 Å-350 Å and is defined to have roughly a
similar redshift coverage.
600 Å coverage
(HE1122-1648, HE2217-2818, Q0055-269
and Q0000-263), the line lists have been divided into
two subsets: a group at higher redshifts and a group at lower redshifts. The rest
of the QSOs do not have enough coverage to make this splitting possible
and provide only one group each. We label the ensemble of these
groups Sample B.
Each group of Sample B
spans 300 Å-350 Å and is defined to have roughly a
similar redshift coverage.
| |
Figure 1:
The
|
| Open with DEXTER | |
To derive
![]() ,
we adopted two methods:
the iterative power-law fit (Schaye et al. 1999,
2000)
and the smoothed b power-law fit
(Bryan & Machacek 2000). From these two power-law
fit methods, we derived
,
we adopted two methods:
the iterative power-law fit (Schaye et al. 1999,
2000)
and the smoothed b power-law fit
(Bryan & Machacek 2000). From these two power-law
fit methods, we derived
![]() and
and
![]() of
Eq. (1) for
k = i or s, where
subscripts "i'' and "s'' indicate the
iterative power-law fit and the smoothed b power-law fit,
respectively. For the iterative power-law fit,
100 bootstrap realizations were averaged with an exclusion
threshold of 0.5 absolute
mean deviation (AMD)
of
Eq. (1) for
k = i or s, where
subscripts "i'' and "s'' indicate the
iterative power-law fit and the smoothed b power-law fit,
respectively. For the iterative power-law fit,
100 bootstrap realizations were averaged with an exclusion
threshold of 0.5 absolute
mean deviation (AMD)![]() . For the smoothed b power-law fit,
a smoothing constant of 3 km s-1 was used for each
subsample having 30 lines and the robust power-law fit was applied.
. For the smoothed b power-law fit,
a smoothing constant of 3 km s-1 was used for each
subsample having 30 lines and the robust power-law fit was applied.
Schaye et al. (2000) used the iterative
power-law fit for
![]() at
2 < z < 3.7 and for
at
2 < z < 3.7 and for
![]() at
3.7 < z < 4.4. Lines with
at
3.7 < z < 4.4. Lines with
![]() ,
however, suffers from
incompleteness due to line blending. For example, at
,
however, suffers from
incompleteness due to line blending. For example, at
![]() ,
lines with
,
lines with
![]() are affected by incompleteness and this threshold
increases with z (cf. Hu et al. 1995; Kim et al.
1997, 2001a, 2001b). Incompleteness causes a
bias in the measurements of
are affected by incompleteness and this threshold
increases with z (cf. Hu et al. 1995; Kim et al.
1997, 2001a, 2001b). Incompleteness causes a
bias in the measurements of
![]() .
Due to the lack of
lines with
.
Due to the lack of
lines with
![]() below this threshold and
below this threshold and
![]() km s-1 (cf. Kim et al. 2001a),
an observationally measured
km s-1 (cf. Kim et al. 2001a),
an observationally measured
![]() value becomes flatter
than its true value.
We have defined different lower
value becomes flatter
than its true value.
We have defined different lower
![]() fitting thresholds at
the various redshifts in order to avoid this bias
(see Fig. 1) and to obtain
a stable estimate of
fitting thresholds at
the various redshifts in order to avoid this bias
(see Fig. 1) and to obtain
a stable estimate of
![]() and
and ![]() at the
fixed column density
at the
fixed column density
![]() ,
,
![]() .
.
Figure 1 shows the
![]() -b diagram at
-b diagram at
![]() ,
3.3 and 3.8 for Sample A.
The fitted parameters
are listed in Table 2, as well as the
,
3.3 and 3.8 for Sample A.
The fitted parameters
are listed in Table 2, as well as the
![]() ranges
used in the fit.
At higher z, several lines show
a b value smaller than
ranges
used in the fit.
At higher z, several lines show
a b value smaller than
![]() at
at
![]() (shaded area).
In fact,
(shaded area).
In fact,
![]() from the both power-law fits
increases as z decreases.
The slopes
from the both power-law fits
increases as z decreases.
The slopes
![]() at
at ![]() and 3.8
are similar within errors, while the slope
and 3.8
are similar within errors, while the slope
![]() at
at ![]() is flatter than
the one at
is flatter than
the one at ![]() more than
more than ![]() .
Both
slopes shows the lowest value at
.
Both
slopes shows the lowest value at ![]() (see Table 2). Note that, however, the errors from
the bootstrap method are likely to be underestimated (cf.
Schaye et al. 2000).
The close examination of Fig. 1 suggests
that
(see Table 2). Note that, however, the errors from
the bootstrap method are likely to be underestimated (cf.
Schaye et al. 2000).
The close examination of Fig. 1 suggests
that
![]() at
at
![]() might well be overestimated and that the
real
might well be overestimated and that the
real
![]() might be inbetween
might be inbetween
![]() and
and
![]() .
.
We visually compared our
![]() with the results of Schaye et al. (2000; their Fig. 1),
although their sample corresponds to our Sample B.
As shown in Table 2, their
with the results of Schaye et al. (2000; their Fig. 1),
although their sample corresponds to our Sample B.
As shown in Table 2, their
![]() values are larger than our
values are larger than our
![]() values
at similar z with the differences larger at smaller z.
Their
values
at similar z with the differences larger at smaller z.
Their
![]() values appear to be flatter than our values
at all z, likely caused by their lack of accounting for
incompleteness of observed lines.
values appear to be flatter than our values
at all z, likely caused by their lack of accounting for
incompleteness of observed lines.
![\begin{figure}
\par\includegraphics[width=6.6cm,clip]{1844Kimf2.eps}\end{figure}](/articles/aa/full/2002/09/aa1844/Timg147.gif) |
Figure 2:
Slopes
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1844Kimf3.eps}\end{figure}](/articles/aa/full/2002/09/aa1844/Timg148.gif) |
Figure 3:
Slopes
|
| Open with DEXTER | |
Figure 2 shows
![]() and
and
![]() as a function of the lower
as a function of the lower
![]() threshold
threshold
![]() for Sample A.
The lack of lines due to incompleteness results in flatter
for Sample A.
The lack of lines due to incompleteness results in flatter
![]() at lower
at lower
![]() .
When the lower
.
When the lower
![]() threshold increases so that incompleteness
does not affect the
threshold increases so that incompleteness
does not affect the
![]() -b distribution severely,
-b distribution severely,
![]() becomes stabilized (the lower
becomes stabilized (the lower
![]() at
at
![]() and 3.3, and the lower
and 3.3, and the lower
![]() at
at
![]() ). If the available
lines in the fit, however, become too small for higher
). If the available
lines in the fit, however, become too small for higher
![]() ,
,
![]() becomes rather ill-defined. On the other hand, the
lower
becomes rather ill-defined. On the other hand, the
lower
![]() does not affect the
does not affect the
![]() values since
values since
![]() at
at
![]() behaves more like a pivotal point. The slopes
behaves more like a pivotal point. The slopes
![]() and
and
![]() from the smoothed b power-law fit
also show similar behaviors.
from the smoothed b power-law fit
also show similar behaviors.
Figure 3 shows
![]() and
and
![]() as a function of z for the individual
members of Sample B (open symbols), the averaged values from Sample B
(filled triangles) and Sample A (filled symbols).
The members of Sample B show the large fluctuation of
as a function of z for the individual
members of Sample B (open symbols), the averaged values from Sample B
(filled triangles) and Sample A (filled symbols).
The members of Sample B show the large fluctuation of
![]() and
and
![]() even at the similar z (see Table 2).
With more lines
available to sharpen the lower cutoff envelope,
even at the similar z (see Table 2).
With more lines
available to sharpen the lower cutoff envelope,
![]() becomes steeper than the ones derived from the individual
members using a smaller number of lines,
possibly approaching asymptotic values (Sample A: filled circles, filled
squares and filled diamonds). For both Sample A and Sample B averaged (filled
triangles),
becomes steeper than the ones derived from the individual
members using a smaller number of lines,
possibly approaching asymptotic values (Sample A: filled circles, filled
squares and filled diamonds). For both Sample A and Sample B averaged (filled
triangles),
![]() shows the lowest value at
shows the lowest value at
![]() ,
although uncertainties for Sample B averaged are
rather large at
,
although uncertainties for Sample B averaged are
rather large at
![]() and 3.8.
While the 1
and 3.8.
While the 1![]() is 0.037 at
is 0.037 at
![]() ,
it becomes twice
as large as that at
,
it becomes twice
as large as that at
![]() and 3.8. This larger fluctuation
at z > 3 is caused in part by a smaller data size and in part by
the cosmic variance. The fluctuation
at
and 3.8. This larger fluctuation
at z > 3 is caused in part by a smaller data size and in part by
the cosmic variance. The fluctuation
at
![]() is mostly caused by different sightlines.
A single,
long
sightline does not show any significant difference between the lower-zpart and the higher-z part, such as HE1122-1648 and
HE2217-2818. On the other hand,
at
is mostly caused by different sightlines.
A single,
long
sightline does not show any significant difference between the lower-zpart and the higher-z part, such as HE1122-1648 and
HE2217-2818. On the other hand,
at
![]() and 3.8, even a single, long sightline shows
a difference between the lower-z part and the higher-z part more
than 3
and 3.8, even a single, long sightline shows
a difference between the lower-z part and the higher-z part more
than 3![]() (see Sect. 3.3 for more discussions).
(see Sect. 3.3 for more discussions).
Similarly,
![]() derived from a larger number of lines
is smaller,
possibly approaching asymptotic values
(Sample A: filled circles, filled squares and filled diamonds). Both
the
derived from a larger number of lines
is smaller,
possibly approaching asymptotic values
(Sample A: filled circles, filled squares and filled diamonds). Both
the
![]() values from Sample A and
Sample B averaged (filled triangles)
increase as z decreases, although the uncertainties for Sample B
averaged are rather large. Note again that the larger fluctuation
of
values from Sample A and
Sample B averaged (filled triangles)
increase as z decreases, although the uncertainties for Sample B
averaged are rather large. Note again that the larger fluctuation
of
![]() at
at
![]() and 3.8
(keep in mind the smaller sample sizes at z > 3 at the same time).
The smoothed b power-law fit also produces the large fluctuations
of
and 3.8
(keep in mind the smaller sample sizes at z > 3 at the same time).
The smoothed b power-law fit also produces the large fluctuations
of
![]() and
and
![]() for the individual
members
of Sample B (see Table 2).
for the individual
members
of Sample B (see Table 2).
Our
![]() and
and
![]() for Sample A
are not consistent with the Schaye et al. values by more than
for Sample A
are not consistent with the Schaye et al. values by more than
![]() .
Our
.
Our
![]() and
and
![]() for Sample B, however,
are completely in agreement with theirs.
This result shows that
deriving
for Sample B, however,
are completely in agreement with theirs.
This result shows that
deriving
![]() and
and
![]() depends largely on the number of lines in the fit and is
subject to the cosmic variance.
Experiments with the fitted line parameters show that in general
more than 200 lines in the fit stabilizes the results (cf. Schaye et al.
1999).
The large fluctuation found from sightline to sightline in similar
redshift
ranges using the number of lines smaller than 200
could explain in part the previous contradictory conclusions
on the evolution of
depends largely on the number of lines in the fit and is
subject to the cosmic variance.
Experiments with the fitted line parameters show that in general
more than 200 lines in the fit stabilizes the results (cf. Schaye et al.
1999).
The large fluctuation found from sightline to sightline in similar
redshift
ranges using the number of lines smaller than 200
could explain in part the previous contradictory conclusions
on the evolution of
![]() and
and
![]() ,
which
were usually based on a small number of lines and of sightlines.
,
which
were usually based on a small number of lines and of sightlines.
There are several known voids (or regions devoid of
absorption lines with
![]() )
in the present data.
One void (
)
in the present data.
One void (
![]() )
towards Q0302-003,
two (
)
towards Q0302-003,
two (
![]() and 3.3) towards Q0055-269
and three (
and 3.3) towards Q0055-269
and three (
![]() ,
2.2 and 2.3) towards HE2217-2818
have been identified.
The regions containing voids of Q0302-003 and
Q0055-269 show a flatter
,
2.2 and 2.3) towards HE2217-2818
have been identified.
The regions containing voids of Q0302-003 and
Q0055-269 show a flatter
![]() by more than 7
by more than 7![]() (two lower squares at
(two lower squares at
![]() in the upper panel of Fig. 3)
and a higher
in the upper panel of Fig. 3)
and a higher
![]() by more than
by more than ![]() (two higher
squares at
(two higher
squares at
![]() in the lower panel of Fig. 3) compared to
the ones derived from Q0055-269 without the voids.
The forest of HE2217-2818, however, does not
show any significant difference between the regions with the voids
and without the voids. Similarly, the HE1122-1648 forest
without any recognizable voids does not show any significant
difference between the lower-z part and
the higher-z part of the spectrum.
in the lower panel of Fig. 3) compared to
the ones derived from Q0055-269 without the voids.
The forest of HE2217-2818, however, does not
show any significant difference between the regions with the voids
and without the voids. Similarly, the HE1122-1648 forest
without any recognizable voids does not show any significant
difference between the lower-z part and
the higher-z part of the spectrum.
Even though voids are produced by the enhanced radiations from
local sources, the increase
of the H I photoionizing photons in voids
does not increase significantly the
temperature of the forest as whole (Haehnelt & Steinmetz 1998).
A fixed
![]() ,
however,
corresponds to a higher overdensity due to the increased
photoionization.
From the equation of state, a higher overdensity means a
higher temperature. Therefore, if voids are produced by enhanced
ionizations, there should be an increase of
,
however,
corresponds to a higher overdensity due to the increased
photoionization.
From the equation of state, a higher overdensity means a
higher temperature. Therefore, if voids are produced by enhanced
ionizations, there should be an increase of
![]() and a decrease of
and a decrease of
![]() compared to the
forest without any extra heating sources at similar z (Haehnelt & Steinmetz
1998; Schaye et al. 1999).
compared to the
forest without any extra heating sources at similar z (Haehnelt & Steinmetz
1998; Schaye et al. 1999).
The lack of a significant
difference in
![]() and
and
![]() from the HE2217-2818 forest at
from the HE2217-2818 forest at
![]() suggests
that the origin of the voids towards HE2217-2818
is different. This could be due to a density fluctuation (Heap et al.
2000) and/or due to a shock heating by galactic infalls or
by galactic winds (Theuns et al. 2001a).
suggests
that the origin of the voids towards HE2217-2818
is different. This could be due to a density fluctuation (Heap et al.
2000) and/or due to a shock heating by galactic infalls or
by galactic winds (Theuns et al. 2001a).
Simulations often show that some Ly![]() lines are
broadened by shock heating (Bryan & Machacek 2000;
Theuns et al. 2001a).
They also show that shock heating is not very
important at z > 2 for the lower column density forest considered
here.
In addition, the cutoff b method
is less sensitive than other methods to shock-heated gas
(cf. Theuns et al. 2001b).
lines are
broadened by shock heating (Bryan & Machacek 2000;
Theuns et al. 2001a).
They also show that shock heating is not very
important at z > 2 for the lower column density forest considered
here.
In addition, the cutoff b method
is less sensitive than other methods to shock-heated gas
(cf. Theuns et al. 2001b).
One of the other main candidates for the fluctuations of
![]() and
and
![]() is
the He II reionization at
is
the He II reionization at ![]() (Haehnelt & Steinmetz 1998; Songaila 1998;
Schaye et al. 1999).
(Haehnelt & Steinmetz 1998; Songaila 1998;
Schaye et al. 1999).
There have been various claims
on a possible He II reionization at ![]() from observations
(Reimers et al. 1997; Songaila 1998;
Heap et al. 2000; Kriss et al. 2001).
One of the consequences of the He II reionization
is an increase of the temperature of the Ly
from observations
(Reimers et al. 1997; Songaila 1998;
Heap et al. 2000; Kriss et al. 2001).
One of the consequences of the He II reionization
is an increase of the temperature of the Ly![]() forest
(Haehnelt & Steinmetz 1998).
In fact, various theoretical models have predicted
a
forest
(Haehnelt & Steinmetz 1998).
In fact, various theoretical models have predicted
a
![]() (thus
a flatter
(thus
a flatter
![]() )
and a higher
)
and a higher ![]() (thus a higher
(thus a higher
![]() )
when the He III bubbles surrounding the ionizing sources
overlap and increase the radiations in the IGM
(Haehnelt & Steinmetz 1998; Ricotti et al. 2000;
Schaye et al. 2000).
)
when the He III bubbles surrounding the ionizing sources
overlap and increase the radiations in the IGM
(Haehnelt & Steinmetz 1998; Ricotti et al. 2000;
Schaye et al. 2000).
To study the effect on the Ly![]() forest caused by the
He II reionization, we re-grouped the individual members
of Sample B. For each z bin, individual members were divided into two
subgroups according to their redshift ranges, i.e. a lower-z part and
a higher-z part. This method of grouping has been
taken since the absorption
lines from the same sightline might be correlated. The number of lines at
each subgroup is sampled to be similar (see Table 2).
forest caused by the
He II reionization, we re-grouped the individual members
of Sample B. For each z bin, individual members were divided into two
subgroups according to their redshift ranges, i.e. a lower-z part and
a higher-z part. This method of grouping has been
taken since the absorption
lines from the same sightline might be correlated. The number of lines at
each subgroup is sampled to be similar (see Table 2).
There is no significant difference in
![]() and
and
![]() between
between
![]() and
and
![]() .
There is, however, a significant difference
by more than
.
There is, however, a significant difference
by more than ![]() 3
3![]() between the lower-z and the higher-z parts at
between the lower-z and the higher-z parts at
![]() and at
and at
![]() .
The slope
.
The slope
![]() decreases at lower z for each bin at z > 3,
while the
decreases at lower z for each bin at z > 3,
while the
![]() increases. In short, along each line of sight at z > 3,
increases. In short, along each line of sight at z > 3,
![]() decreases and
decreases and
![]() increases
at z decreases, as expected from the He II reionization
at
increases
at z decreases, as expected from the He II reionization
at ![]() .
This trend, however, does not continue at z < 3,
i.e. the HE1122-1648 forest and the HE2217-2818
forest do not show the similar behavior. Theuns et al. (2001b)
find a similar behavior of b values from the wavelet analysis
using the same data presented here.
This is interpreted as a result of HeII reionization at
.
This trend, however, does not continue at z < 3,
i.e. the HE1122-1648 forest and the HE2217-2818
forest do not show the similar behavior. Theuns et al. (2001b)
find a similar behavior of b values from the wavelet analysis
using the same data presented here.
This is interpreted as a result of HeII reionization at
![]() .
They do find, however, a cold region, i.e. a region with
a lower average b values than the adjacent regions along HE2217-2818.
.
They do find, however, a cold region, i.e. a region with
a lower average b values than the adjacent regions along HE2217-2818.
Deriving the cutoff Doppler
parameters using a small
number of lines introduces a large scatter (Fig. 3). Therefore,
a flatter
![]() and a higher
and a higher
![]() shown at the lower-z part of the bins at z > 3 (
shown at the lower-z part of the bins at z > 3 (![]() 3.1 and
3.6)
might be an artifact of the small number of
lines in the fit. More available lines in the fit, however, tends to
increase
3.1 and
3.6)
might be an artifact of the small number of
lines in the fit. More available lines in the fit, however, tends to
increase
![]() and to decrease
and to decrease
![]() as seen in Sect. 3.2, contrary to this result.
as seen in Sect. 3.2, contrary to this result.
The
![]() -b distributions at
-b distributions at
![]() and
and
![]() show a lack of lines with
show a lack of lines with
![]() and
and ![]() km s-1with respect to the ones
at
km s-1with respect to the ones
at
![]() and 3.9, while the
and 3.9, while the
![]() -b distributions
for higher-
-b distributions
for higher-
![]() lines are similar (the figures not shown).
This lack of
lower-
lines are similar (the figures not shown).
This lack of
lower-
![]() and lower-b lines results in a
flatter
and lower-b lines results in a
flatter
![]() and a higher
and a higher
![]() at
at
![]() and 3.6.
This, however, can not be caused by incompleteness due to
line blending.
The number of lower-
and 3.6.
This, however, can not be caused by incompleteness due to
line blending.
The number of lower-
![]() lines are
similar at
lines are
similar at
![]() and
and
![]() ,
and at
,
and at
![]() and
and
![]() ,
i.e. b values corresponding
to lower-
,
i.e. b values corresponding
to lower-
![]() lines are higher at
lines are higher at
![]() and
and
![]() than those at
than those at
![]() and
and
![]() .
In addition,
line blending is more severe at higher z and should have resulted in
a lack of lower-
.
In addition,
line blending is more severe at higher z and should have resulted in
a lack of lower-
![]() and lower-b lines at
and lower-b lines at
![]() and
and
![]() rather than at
rather than at
![]() and
and
![]() as observed. What is observed at
as observed. What is observed at
![]() and
and
![]() shows the opposite behavior expected from line
blending. In fact, the lower-
shows the opposite behavior expected from line
blending. In fact, the lower-
![]() and higher-b lines
seen at
and higher-b lines
seen at
![]() and at
and at
![]() are expected from the He II reionization since it has a greater
effect on the lower-
are expected from the He II reionization since it has a greater
effect on the lower-
![]() forest than on the
higher-
forest than on the
higher-
![]() forest (Theuns 2001, private communication).
forest (Theuns 2001, private communication).
Songaila (1998) found that there is
an abrupt, sharp discontinuity in the
ratio of Si IV column density to C IV column density,
![]() /
/
![]() ,
at
,
at
![]() ,
below which
,
below which
![]() /
/
![]() is always
less than
is always
less than ![]() 0.07.
The observed
0.07.
The observed
![]() /
/
![]() by
Songaila (1998) suggests that the UV background is softer than
a QSO-dominated background at z > 3 and becomes harder as expected
from a QSO-dominated background at z < 3. This observation
has been interpreted
as the complete He II reionization by
by
Songaila (1998) suggests that the UV background is softer than
a QSO-dominated background at z > 3 and becomes harder as expected
from a QSO-dominated background at z < 3. This observation
has been interpreted
as the complete He II reionization by ![]() ,
i.e.
the overlap of the He III bubbles.
,
i.e.
the overlap of the He III bubbles.
Figure 4 shows
![]() /
/
![]() of the
Ly
of the
Ly![]() forest
at
forest
at
![]() as a function of z
from the QSOs in Table 1 except from
Q0000-263 (Kim et al. 2001, in preparation).
We only include the H I systems having higher Lyman lines
other than Ly
as a function of z
from the QSOs in Table 1 except from
Q0000-263 (Kim et al. 2001, in preparation).
We only include the H I systems having higher Lyman lines
other than Ly![]() ,
such as Ly
,
such as Ly![]() ,
Ly
,
Ly![]() ,
etc. This selection
enables us to estimate an accurate H I column density and to
assign Si IV and C IV to a H I line more reliably.
Note that there are no data points at
2.6 < z < 2.9 at which the discontinuity of
,
etc. This selection
enables us to estimate an accurate H I column density and to
assign Si IV and C IV to a H I line more reliably.
Note that there are no data points at
2.6 < z < 2.9 at which the discontinuity of
![]() /
/
![]() has been reported to be the largest. Although the bulk of the forest
shows lower
has been reported to be the largest. Although the bulk of the forest
shows lower
![]() /
/
![]() at z < 2.6, there are the forest lines with
at z < 2.6, there are the forest lines with
![]() /
/
![]() larger than 0.07.
The similar results have been reported at z > 2 by
Boksenberg et al. (1998). Bear in mind that
no specific H I column density range used in
their Fig. 1 is given in their paper. In addition, note that their
results are based on the individual, fitted components, while ours are
based on the integrated absorption lines. Using
the component-by-component analysis introduces an additional scatter in the
diagram due to the different velocity structures in Si IV
and C IV. The number of components for one integrated system
in our data is in general from 1 to 3. The component-by-component
analysis on our data also shows the similar trend found in Fig. 4
from the integrated profiles.
larger than 0.07.
The similar results have been reported at z > 2 by
Boksenberg et al. (1998). Bear in mind that
no specific H I column density range used in
their Fig. 1 is given in their paper. In addition, note that their
results are based on the individual, fitted components, while ours are
based on the integrated absorption lines. Using
the component-by-component analysis introduces an additional scatter in the
diagram due to the different velocity structures in Si IV
and C IV. The number of components for one integrated system
in our data is in general from 1 to 3. The component-by-component
analysis on our data also shows the similar trend found in Fig. 4
from the integrated profiles.
Our observations do not suggest any abrupt change in
![]() /
/
![]() at
1.6 < z < 3.6, i.e. no abrupt change in the
softness parameter in general. This result suggests that
some forest clouds are exposed to a soft UV background at
z < 2.6. The lack of a sharp change
in
at
1.6 < z < 3.6, i.e. no abrupt change in the
softness parameter in general. This result suggests that
some forest clouds are exposed to a soft UV background at
z < 2.6. The lack of a sharp change
in
![]() /
/
![]() at
at ![]() does not mean, however, that the He II reionization
did not occur at
does not mean, however, that the He II reionization
did not occur at ![]() .
Rather, our
.
Rather, our
![]() /
/
![]() indicates that
indicates that
![]() /
/
![]() might not be a good observational
tool to probe the He II reionization. What it probes is
a softness parameter of the UV background. Increasing evidences
of the contribution to the UV background from local, high-z galaxies
would explain our high
might not be a good observational
tool to probe the He II reionization. What it probes is
a softness parameter of the UV background. Increasing evidences
of the contribution to the UV background from local, high-z galaxies
would explain our high
![]() /
/
![]() at z < 2.6 without any
difficulty (Giroux & Shull 1997; Shull et al. 1999;
Bianchi et al. 2001;
Steidel et al.
2001). In addition,
the lack of strong z-evolution of
at z < 2.6 without any
difficulty (Giroux & Shull 1997; Shull et al. 1999;
Bianchi et al. 2001;
Steidel et al.
2001). In addition,
the lack of strong z-evolution of
![]() found
for
found
for
![]() at z > 3is in agreement with the lack of strong evolution of
at z > 3is in agreement with the lack of strong evolution of
![]() /
/
![]() at
at
![]() .
In short,
the He II reionization at
.
In short,
the He II reionization at ![]() (Reimers et al. 1997; Heap et al. 2000;
Smette et al. 2002) shows its impact on the Ly
(Reimers et al. 1997; Heap et al. 2000;
Smette et al. 2002) shows its impact on the Ly![]() forest mainly at
forest mainly at
![]() and might be very inhomogeneous.
Its strength might not be as strong as previously suggested and
and might be very inhomogeneous.
Its strength might not be as strong as previously suggested and
![]() /
/
![]() might not be a best observational tool
to probe the He II reionization.
might not be a best observational tool
to probe the He II reionization.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1844Kimf4.eps}\end{figure}](/articles/aa/full/2002/09/aa1844/Timg176.gif) |
Figure 4:
The ratio of
|
| Open with DEXTER | |
Converting
![]() and
and
![]() to the corresponding
to the corresponding
![]() and T0 depends on many uncertain parameters, such as
the UV background and the reionization history.
If the UV background is dominated by QSOs without any extra heating,
T0 decreases and
and T0 depends on many uncertain parameters, such as
the UV background and the reionization history.
If the UV background is dominated by QSOs without any extra heating,
T0 decreases and
![]() increases as z decreases, until they approach
asymptotic values. The
increases as z decreases, until they approach
asymptotic values. The
![]() value, however, still
increases with decreasing z, until it approaches an asymptotic
value and finally decreases again at z < 2 (Schaye et al. 1999).
value, however, still
increases with decreasing z, until it approaches an asymptotic
value and finally decreases again at z < 2 (Schaye et al. 1999).
Instead of converting
to T0, we compare our
![]() with Figs. 3 and 4 of Schaye et al. (2000) from their
simulations assuming the QSO-dominated Haardt-Madau UV background,
with Figs. 3 and 4 of Schaye et al. (2000) from their
simulations assuming the QSO-dominated Haardt-Madau UV background,
![]() (Haardt
& Madau 1996)
(Haardt
& Madau 1996)![]() .
Our
.
Our
![]() is in agreement with their simulated
is in agreement with their simulated
![]() values without extra He II heating,
although the difference increases as zdecreases (ours being a factor of 1.1 lower at
values without extra He II heating,
although the difference increases as zdecreases (ours being a factor of 1.1 lower at ![]() ).
It is not clear what causes their numerical simulations without
the He II reionization produce their
).
It is not clear what causes their numerical simulations without
the He II reionization produce their
![]() similar to ours which suggest the extra heating.
One of the explanations could be a weaker effect on the forest
from the He II reionization than their simulations suggest.
When
similar to ours which suggest the extra heating.
One of the explanations could be a weaker effect on the forest
from the He II reionization than their simulations suggest.
When ![]() is converted from the same simulations (their Fig. 2),
is converted from the same simulations (their Fig. 2),
![]() decrease as z decreases.
decrease as z decreases.
For
![]() ,
we assume the conversion law between
,
we assume the conversion law between
![]() and
and ![]() by
Schaye (2001) assuming
by
Schaye (2001) assuming
![]() and
and
![]() for
thermally broadened lines.
The conversion law is defined by
for
thermally broadened lines.
The conversion law is defined by
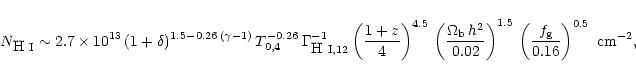 | (2) |
where
![]() K,
the H I photoionization rate
K,
the H I photoionization rate
![]() s-1,
s-1,
![]() is the baryon density, h is the Hubble constant divided by 100,
and
is the baryon density, h is the Hubble constant divided by 100,
and ![]() is the fraction of the mass in gas (Schaye
2001). We read
is the fraction of the mass in gas (Schaye
2001). We read ![]() from Fig. 3 of
Schaye et al. (2000) and
from Fig. 3 of
Schaye et al. (2000) and
![]() from
Fig. 8 of Haardt
& Madau (1996), while we assume
from
Fig. 8 of Haardt
& Madau (1996), while we assume
![]() and
and
![]() .
At
.
At
![]() ,
3.3 and 3.8,
,
3.3 and 3.8,
![]() ,
0.386 and 0.441. Assuming
,
0.386 and 0.441. Assuming
![]() ,
there is no clear z-evolution of
,
there is no clear z-evolution of
![]() within large
uncertainties. Our values and Schaye et al.'s
(
within large
uncertainties. Our values and Schaye et al.'s
(
![]() 0.4, 0.35 and 0.25 at
0.4, 0.35 and 0.25 at
![]() ,
3.3 and 3.8
assuming
,
3.3 and 3.8
assuming
![]() )
agree at
)
agree at ![]() 2.1, 3.3, while
our value is a factor of 1.8 larger than theirs at <z> = 3.8.
Our
2.1, 3.3, while
our value is a factor of 1.8 larger than theirs at <z> = 3.8.
Our
![]() values agree with those of McDonald et al.
at the similar z ranges within uncertainties, although their
simulations do not assume
values agree with those of McDonald et al.
at the similar z ranges within uncertainties, although their
simulations do not assume
![]() .
.
Using the new, large dataset
from high S/N, high resolution VLT/UVES
data combined with one Keck/HIRES QSO in the literature, the minimum
cutoff Doppler parameter as a function of
![]() ,
,
![]() ,
of the Ly
,
of the Ly![]() forest
has been derived at
forest
has been derived at ![]() 2.1, 3.3 and 3.8.
We have found:
2.1, 3.3 and 3.8.
We have found:
Acknowledgements
We are indebted to M. Dessauges-Zavadsky for support during the observations of Q0055-269. We thank Martin Haehnelt, Joop Schaye, Tom Theuns and Saleem Zaroubi for insightful discussions. TSK thanks Dave Jewitt, Bob Carswell and Glenn Morris for their careful reading of the manuscript. This work has been conducted with partial support by the Research Training Network "The Physics of the Intergalactic Medium'' set up by the European Community under the contract HPRN-CT2000-00126 RG29185 and by ASI through contract ARS-98-226.