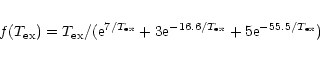Up: Neutral atomic carbon in
In a number of studies (e.g. Schilke et al. 1993; Tauber et al. 1995;
Petitpas & Wilson 1998) column densities have been calculated assuming
[CI] and CO emission to occur under optically thin LTE conditions in the
high-temperature limit.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{cifig_3.ps}\end{figure}](/articles/aa/full/2002/07/aa1620/Timg116.gif) |
Figure 3:
Model line ratio
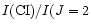 - -
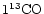 )
versus )
versus
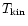 resulting for equal column densities
resulting for equal column densities
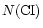 /d /d
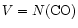 /dV
(solid lines). Curves for a range of total gas densities are marked in
particles per cc. Dashed line: the ratio /dV
(solid lines). Curves for a range of total gas densities are marked in
particles per cc. Dashed line: the ratio
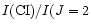 - -
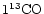 )
versus )
versus
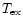 ,
likewise requiring equal column densities ,
likewise requiring equal column densities
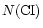 /d /d
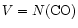 /dV but assuming optically thin LTE conditions. /dV but assuming optically thin LTE conditions. |
From Eqs. (1) and (2) by Tauber et al. (1995), it follows that:
where
while we assume an isotopic abundance
![$A^{12}_{13} = [{\rm ^{12}CO}]/[{\rm ^{13}CO}]$](/articles/aa/full/2002/07/aa1620/img119.gif) = 40
(cf. Mauersberger & Henkel 1993; Henkel et al. 1998).
In Fig. 3 we have marked by a dashed line the expected line intensity ratios
for the case
= 40
(cf. Mauersberger & Henkel 1993; Henkel et al. 1998).
In Fig. 3 we have marked by a dashed line the expected line intensity ratios
for the case
![$N[{\rm CI}])/N({\rm CO}) = 1$](/articles/aa/full/2002/07/aa1620/img120.gif) .
In order to verify the correctness of the
assumptions of low optical depth and LTE, we have used the Leiden radiative
transfer models described by Jansen (1995) and Jansen et al. (1994) to
calculate for gas volume densities ranging from
.
In order to verify the correctness of the
assumptions of low optical depth and LTE, we have used the Leiden radiative
transfer models described by Jansen (1995) and Jansen et al. (1994) to
calculate for gas volume densities ranging from
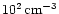 to
to
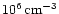 the [CI]/
the [CI]/
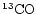 line intensity ratio corresponding to unit column density
ratios. The calculation was performed for a representative value of the
column density,
line intensity ratio corresponding to unit column density
ratios. The calculation was performed for a representative value of the
column density,
![$N[{\rm CI}]$](/articles/aa/full/2002/07/aa1620/img123.gif) /d
/d
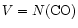 /d
/d
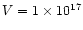 cm
cm
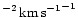 (cf. Israel & Baas 2001). Note that in this calculation,
the temperature parameter is the kinetic temperature
(cf. Israel & Baas 2001). Note that in this calculation,
the temperature parameter is the kinetic temperature
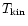 instead of the excitation temperature
instead of the excitation temperature
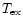 .
For neutral carbon,
the two are not very different under the conditions considered, but for
.
For neutral carbon,
the two are not very different under the conditions considered, but for
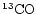 the excitation temperature is generally much lower than the kinetic
temperature over most of the relevant range. Under LTE conditions,
the [CI]/
the excitation temperature is generally much lower than the kinetic
temperature over most of the relevant range. Under LTE conditions,
the [CI]/
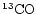 ratio continuously increases with temperature
ratio continuously increases with temperature
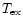 .
In contrast, the radiative transfer calculation shows that this ratio is
only weakly dependent on temperature above
.
In contrast, the radiative transfer calculation shows that this ratio is
only weakly dependent on temperature above
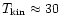 K, and
in fact decreases slowly with increasing temperature for densities up to
K, and
in fact decreases slowly with increasing temperature for densities up to
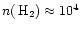 .
As Fig. 3 illustrates, the assumption of comparable
excitation temperatures for
.
As Fig. 3 illustrates, the assumption of comparable
excitation temperatures for
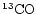 and [CI] is valid only for very high
densities
and [CI] is valid only for very high
densities
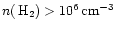 which are unlikely to apply to our observed
sample.
which are unlikely to apply to our observed
sample.


Up: Neutral atomic carbon in
Copyright ESO 2002
![\begin{eqnarray*}I([{\rm CI}])/I({\rm ^{13}CO}) = 0.0063\, A^{12}_{13}\, f(T_{\rm ex})\, N[{\rm CI}])/N({\rm CO})
\end{eqnarray*}](/articles/aa/full/2002/07/aa1620/img117.gif)