![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{h3222f7.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg162.gif) |
Figure 7: Offsets between optical and X-ray positions. The extended X-ray source XMMU J122017.9+752212 is not shown. Symbols as in 3. |
With the sample of X-ray sources whose optical counterparts have been positively identified (including the ones below our flux limit), we check how good the astrometry of the XMM-Newton data was. We then analyzed the offsets of the optical position with respect to the X-ray position. These are shown in Fig. 7, where error bars are just the X-ray positional errors, which by far dominate over the optical position ones.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{h3222f7.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg162.gif) |
Figure 7: Offsets between optical and X-ray positions. The extended X-ray source XMMU J122017.9+752212 is not shown. Symbols as in 3. |
An obvious feature to note is that, apart from the source XMMU J122017.9+752212 which is extended both in X-rays and in the optical (NGC 4291), there is no obvious trend of offsets being larger for any source class. In particular the sources classified as NELGs (which in fact are all AGNs) are unlikely to be chance coincidences, as in that case they would exhibit larger offsets with respect to the X-ray sources.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm]{h3222f8.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg163.gif) |
Figure 8: Histogram of offsets (Optical - X-ray) scaled to the corresponding statistical uncertainty in the X-ray position. The best fit accounting for systematics is also shown. |
Figure 8 shows the histogram of these offsets
normalized to their corresponding statistical errors. Assuming that position
errors are well reproduced by a Gaussian, this normalized offset xshould be distributed as
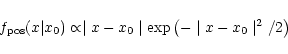 |
(1) |
A closer inspection of the sources showing residual astrometric systematics shows that all of them are in the Mkn 205 field, all of them are relatively bright and only one of them is relatively close to the centre of the field (but then close enough to the Mkn 205 point-spread function tail). We do not fully understand the reason for this, but perhaps it might be related to the overall astrometric solution being dominated by some spurious matches of X-ray sources fainter than the ones used in our survey. The residuals are, however, so small that they are irrelevant for a high galactic latitude field. Much more care should be taken, however, in galactic plane fields where the density of optical sources is much larger and chance associations might produce a completely wrong astrometric solution. We suggest in this case to use a very limited number of secure identifications to derive a first astrometric correction and then iterate as the number of identified sources grows.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3222f9.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg166.gif) |
Figure 9: i'-magnitude vs. X-ray flux for this sample. Symbols as in 3. |
As expected, the majority of the identified X-ray sources are
extragalactic (only 1 galactic AC), and in particular AGN. Figure 9 shows the optical to X-ray relation for the X-ray
sources. We see that most, if not all, of the BLAGNs will be
identified in the medium sensitivity survey (i.e. at a flux limit of
![]() )
down to
)
down to
![]() .
NELGs and other galaxies are typically
fainter, but we expect to identify large fractions of them within the
AXIS resources. We can conclude from this pilot study that >
.
NELGs and other galaxies are typically
fainter, but we expect to identify large fractions of them within the
AXIS resources. We can conclude from this pilot study that >![]() of
the medium sample can be identified with the AXIS programme.
of
the medium sample can be identified with the AXIS programme.
One remarkable feature of this survey is that we have found no clusters of galaxies as counterparts of the identified X-ray sources. Using the source counts from the ROSAT Deep Cluster Survey (Rosati et al. 1998) we would have expected <2-3 clusters in our sample. We must further stress that there are no cluster candidates in the unidentified sources, down to the sensitivity limits of the optical images. Actually, the sliding box algorithm used to search for sources in the XMM-Newton images is not optimized for the detection of extended sources. Therefore we do not expect to be complete in groups and clusters. In fact, extended sources in XMM-Newton images are the subject of on-going parallel studies within the XMM-Newton Survey Science Centre activities.
We have cross-correlated the X-ray source positions with the NVSS
radio survey (Condon et al. 1998). No coincidences closer than 10
arcsec are found for the flux-limited sample. The only radio source
within 30 arcsec of an X-ray source is a faint source of 2.4 mJy, just
below the completeness level of NVSS, 14.4 arcsec away from XMMU
J010400.9-064949. The NVSS positional uncertainty for a source this
faint (rms about 7 arcsec), when combined with the astrometric
accuracy of our X-ray sources (Sect. 5.1) make it
unlikely that this is a true association. For the full sample of 89
sources found by our source-searching algorithms, the number of
coincidences within 30 arcsec increases from zero to one, with a
source of 2.7 mJy being found 7.1 arcsec from an unidentified X-ray
source of
![]() .
Despite the fact that this is likely to be a true
association, preliminary statistics based on about 3000 X-ray sources
from the ChaMP survey (Wilkes et al. 2001; Wilkes & Green 2001,
private communication) find a radio association with NVSS which
increases with X-ray flux, and with which our two XMM-Newton fields
disagree at the 95% confidence level. Work is underway to
investigate the radio properties of larger samples of sources.
.
Despite the fact that this is likely to be a true
association, preliminary statistics based on about 3000 X-ray sources
from the ChaMP survey (Wilkes et al. 2001; Wilkes & Green 2001,
private communication) find a radio association with NVSS which
increases with X-ray flux, and with which our two XMM-Newton fields
disagree at the 95% confidence level. Work is underway to
investigate the radio properties of larger samples of sources.
Figure 10 shows the luminosity-redshift relation for the
extragalactic sources identified in our sample. With the exception of
NGC 4291, which has a luminosity not far from that of a normal galaxy (![]()
![]() ), all the remaining
extragalactic objects have luminosities higher than
), all the remaining
extragalactic objects have luminosities higher than ![]()
![]() ,
so there is no doubt they host an Active
Galactic Nucleus. In particular, all the objects classified as NELGs,
should in reality be called Narrow-line AGNs (NLAGNs). Indeed some (if
not all of them) exhibit [OIII] lines much stronger than [OII] and/or
[NeV] emission lines, all of which are features of a hard non-stellar
ionizing continuum in the narrow-line emitting region.
,
so there is no doubt they host an Active
Galactic Nucleus. In particular, all the objects classified as NELGs,
should in reality be called Narrow-line AGNs (NLAGNs). Indeed some (if
not all of them) exhibit [OIII] lines much stronger than [OII] and/or
[NeV] emission lines, all of which are features of a hard non-stellar
ionizing continuum in the narrow-line emitting region.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3222f10.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg172.gif) |
Figure 10: Luminosity-redshift relation for the extragalactic sources identified in the sample. Symbols as in 3. |
The weighted average hardness ratios for BLAGN are
![]() and
and
![]() .
It is interesting to note that for a single power-law spectrum,
these values correspond to
.
It is interesting to note that for a single power-law spectrum,
these values correspond to
![]() and
and
![]() respectively, i.e., it appears that BLAGN have a hardening in their
spectrum towards high photon energies.
respectively, i.e., it appears that BLAGN have a hardening in their
spectrum towards high photon energies.
It is remarkable, however, that the average spectra of BLAGN do not
appear to be consistent with a single power law spectrum. Indeed,
while HR1 is consistent with an unabsorbed ![]() spectrum, at
harder photon energies HR2 calls for a much flatter X-ray spectrum,
with
spectrum, at
harder photon energies HR2 calls for a much flatter X-ray spectrum,
with
![]() .
A similar result has been recently found by
Pappa et al. (2001) by co-adding ROSAT and ASCA spectra of 21 BLAGN. Our result confirms that this is not due to a mismatch between
ROSAT and ASCA calibrations and amphasizes the power of XMM-Newton
in broad-band X-ray spectral studies.
.
A similar result has been recently found by
Pappa et al. (2001) by co-adding ROSAT and ASCA spectra of 21 BLAGN. Our result confirms that this is not due to a mismatch between
ROSAT and ASCA calibrations and amphasizes the power of XMM-Newton
in broad-band X-ray spectral studies.
The spectral shape that we infer for BLAGN was first empirically
proposed by Schwartz & Tucker (1988) in order to reproduce the XRB
spectrum. The subsequent discovery of a Compton reflection bump in the
X-ray spectrum of Seyfert 1 galaxies (Pounds et al. 1990) suggested that
reflection-dominated AGN (i.e., AGN where >![]() of the observed
X-rays would have been reflected in cold/warm material) could
contribute the bulk of the X-ray background
(Fabian et al. 1990). Although no significant population of such sources
has been detected, it is likely that we are witnessing the effects of
Compton reflection or a similar phenomenon in the average X-ray
spectra of the
of the observed
X-rays would have been reflected in cold/warm material) could
contribute the bulk of the X-ray background
(Fabian et al. 1990). Although no significant population of such sources
has been detected, it is likely that we are witnessing the effects of
Compton reflection or a similar phenomenon in the average X-ray
spectra of the
![]() BLAGN in our sample. If the Compton
reflection bump entering the 4.5-10 keV band is the ultimate reason
for the hard values of HR2, then a trend with redshift should be
seen. In Fig. 11 we plot both hardness ratios HR1 and
HR2 as a function of redshift for the extragalactic objects. No
trend is found in HR1 vs. z for BLAGN, and at best we can only claim
a hint of HR2 becoming higher at high redshifts. That, which would
be expected if Compton reflection is responsible for the hardening of
the spectrum, needs much more data to be confirmed.
BLAGN in our sample. If the Compton
reflection bump entering the 4.5-10 keV band is the ultimate reason
for the hard values of HR2, then a trend with redshift should be
seen. In Fig. 11 we plot both hardness ratios HR1 and
HR2 as a function of redshift for the extragalactic objects. No
trend is found in HR1 vs. z for BLAGN, and at best we can only claim
a hint of HR2 becoming higher at high redshifts. That, which would
be expected if Compton reflection is responsible for the hardening of
the spectrum, needs much more data to be confirmed.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{h3222f11.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg178.gif) |
Figure 11:
Hardness ratios HR1 and HR2 as a function of redshift z. Symbols as in 3. We also plot expected values for single
power law spectra with
|
We only find marginal evidence for the NLAGN having a harder spectrum
than BLAGN (see Fig. 3). Such a trend had been found in
ROSAT surveys (Romero-Colmenero et al. 1996; Almaini et al. 1996). The weighted average
hardness ratios for these objects are
![]() and
and
![]() .
.
![]() agrees with the corresponding value for BLAGNs, but HR1 is slightly
higher, although only at
agrees with the corresponding value for BLAGNs, but HR1 is slightly
higher, although only at ![]()
![]() significance. If we interpret
the marginal difference in terms of a
significance. If we interpret
the marginal difference in terms of a ![]() power-law spectrum
being affected by intrinsic absorption in NLAGN, the inferred column
density is
power-law spectrum
being affected by intrinsic absorption in NLAGN, the inferred column
density is
![]() at a redshift of
z=0.4 where most of the NLAGNs are located.
at a redshift of
z=0.4 where most of the NLAGNs are located.
We must recall that evidence has been accumulated that X-ray photoelectric absorption and optical spectroscopic classification do not appear to have a one-to-one relation. For example hard X-ray sources found in ROSAT surveys contain large fractions of unobscured type 1 QSOs and Seyferts (Page et al. 2001). On the contrary, dusty warm absorbers produce little effect in the X-ray broad-band colours of AGN, but substantially influence their optical appearence. The underlying reason for all these apparent inconsistencies could be the different distributions of atomic gas and dust in the close environment of the AGN central engine (Maiolino et al. 2001), perhaps due to dust sublimation near the center (Granato et al. 1997).
Source XMMU J122017.9+752212 (NGC 4291) deserves further comment. X-ray emission from this galaxy was detected with Einstein (Canizares et al. 1987). Roberts & Warwick (2000) analyzed ROSATHRI images of nearby galaxies and find a nuclear X-ray point source within 6.8 arcsec from the centre of NGC 4291. The extended X-ray emission of this source in the 0.5-4.5 keV XMM-Newton image clearly masks out a part of the sky, which is why we have removed a 1.5 arcmin radius circle around it. However, when this region is examined only in the 2-10 keV band, the diffuse emission disappears. What is then seen is a point source approximately coincident with the nucleus of NGC 4291 and a further 4 sources within the excised region, some of which might possibly be associated with the galaxy. The fact that NGC 4291 presents a point source in its center is a strong suggestion that an active nucleus might be actually hidden in the centre of this optically dull galaxy. A more complete discussion of this interesting galaxy and its environment is beyond the scope of this paper and will be presented elsewhere.
Among the sample of BLAGN we find 2 (XMMU J010328.7-064633 at z=1.82 and XMMU J010316.7-065137 at z=1.91) Broad-Absorption-Line (BAL) QSO (see Figs. 12 and 13). Parameters of the corresponding broad-absorption line systems (based on the CIV line) are listed in Table 8. In particular we have computed the so-called Balnicity index introduced by Weymann et al. (1991) as a way to provide a continuous classification between BAL and non-BAL QSOs. In the context of the sample studied by Weymann et al. (1991) the value of the Balnicity Index is in the low end for XMMU J010316.7-065137 but close to average for XMMU J010328.7-064633.
| Source |
|
|
BI |
| (Å) | (
|
(
|
|
| XMMU J010316.7-065137 | 5 | 19000 | 580 |
| XMMU J010328.7-064633 | 34 | 34000 | 3650 |
BAL QSOs have been practically absent from previous X-ray selected samples. There have been a few exceptions: 1 BAL QSO in the Einstein Medium Sensitivity Survey at z=2.027 (Stocke et al. 1991) and more recently the ELAIS/BeppoSAX survey at z=2.2(Alexander et al. 2001), the Chandra deep field south at z=2.75, (Giacconi et al. 2001) and the survey of ROSAT hard X-ray sources at z=2.21 (Page et al. 2001).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h3222f12.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg185.gif) |
Figure 12: Optical spectra of the BAL QSO XMMU J010328.7-064633 obtained with the ISIS spectrograph on the WHT. Both blue and red arm spectra (which have different channel size) are shown. |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{h3222f13.ps}\end{figure}](/articles/aa/full/2002/05/aah3222/Timg186.gif) |
Figure 13: Optical spectra of the BAL QSO XMMU J010316.7-065137 obtained with the ISIS double spectrograph on the WHT. Both blue and red arm spectra (which have different channel size) are shown. |
The paucity of BAL QSOs in previous X-ray surveys is hardly surprising, as the gas ejected by BAL QSOs which is responsible for the broad absorption lines will efficiently absorb soft X-rays. Previous X-ray missions, mostly sensitive to soft X-rays like Einstein and ROSAT, are expected to have a much reduced sensitivity to BAL QSOs with respect to optical surveys. It is illustrative to notice that the only ROSAT-discovered BAL QSO was found in a selection of hard X-ray spectrum sources.
We find it intriguing that the BAL QSOs have "normal'' values
of HR1:
![]() for XMMU J010328.7-064633 and
for XMMU J010328.7-064633 and
![]() for
XMMU J010316.7-065137 (the average over all sources in the sample is
for
XMMU J010316.7-065137 (the average over all sources in the sample is ![]()
![]() for HR1). Indeed, the high redshift of the two
objects helps to move the intrinsic photoelectric absorption feature
below our detection band (0.5-4.5 keV). Assuming z=1.85, and an
unabsorbed
for HR1). Indeed, the high redshift of the two
objects helps to move the intrinsic photoelectric absorption feature
below our detection band (0.5-4.5 keV). Assuming z=1.85, and an
unabsorbed ![]() power-law spectrum, an intrinsic absorbing column
of
power-law spectrum, an intrinsic absorbing column
of ![]()
![]() increases the value of HR1 from -0.68 in the
absence of intrinsic absorption to -0.61. It is then clear that these
objects cannot have intrinsic columns significantly in excess of
increases the value of HR1 from -0.68 in the
absence of intrinsic absorption to -0.61. It is then clear that these
objects cannot have intrinsic columns significantly in excess of
![]() or otherwise we would see it in their X-ray spectra.
However, these are unusually small values for the absorbing columns in
BAL QSOs. Gallagher et al. (2001) report on ASCA and Chandraobservations of several BAL QSOs, and the inferred absorbing columns
always exceed
or otherwise we would see it in their X-ray spectra.
However, these are unusually small values for the absorbing columns in
BAL QSOs. Gallagher et al. (2001) report on ASCA and Chandraobservations of several BAL QSOs, and the inferred absorbing columns
always exceed
![]() and sometimes by a large
amount. Here we see that low (neutral) column density BAL QSOs do
exist. Perhaps high ionisation and/or partial covering could bring to agreement
the apparent small X-ray absorbing column with a sizeable
CIV broad absorption line.
and sometimes by a large
amount. Here we see that low (neutral) column density BAL QSOs do
exist. Perhaps high ionisation and/or partial covering could bring to agreement
the apparent small X-ray absorbing column with a sizeable
CIV broad absorption line.
A further remarkable fact is that both BAL QSOs lie at the redshift where the distribution of BLAGN peaks. This might be telling us that we are only seeing the tip of the iceberg, i.e., we have only detected BAL QSOs at the redshift where this detection would be more likely (helped indeed by the K-correction discussed above).
What remains to be understood is why BAL QSOs were practically absent
in ROSAT surveys of similar depth (e.g. Boyle et al. 1994). The
sensitivity to higher X-ray photons of our current survey (0.5-4.5 keV)
with respect to the standard 0.5-2 keV ROSAT band does not make a
big difference: for a z=1.85, intrinsically absorbed (
![]() )
power-law (
)
power-law (![]() )
QSO spectrum, only
)
QSO spectrum, only ![]()
![]() of
the counts from the source fall in the 2-4.5 keV band in EPIC pn. A source
with that spectrum at our survey limit, would have a 0.5-2 keV flux
slightly above
of
the counts from the source fall in the 2-4.5 keV band in EPIC pn. A source
with that spectrum at our survey limit, would have a 0.5-2 keV flux
slightly above ![]()
![]() and would have been therefore detectable in the
so-called ROSAT deep survey (Boyle et al. 1994).
and would have been therefore detectable in the
so-called ROSAT deep survey (Boyle et al. 1994).
Copyright ESO 2002