2 The X-ray data

2.1 XMM-Newton observations

The identifications presented in this paper correspond to X-ray sources serendipitously found in 2 XMM-Newton images (G133-69 Pos_2 and Mkn 205). G133-69 Pos_2 was observed as a Guaranteed Time observation to probe the galactic halo using X-ray shadows. It consists of a single data set totalling 16 ks of good exposure time in full frame mode. The Mkn 205 field was observed as a calibration observation, and consists of 3 exposures of 17 ks each. One of these is in large-window mode (for the EPIC pn camera) which only covers half of the field of view. The remaining 2 data sets are in full window mode, and we merged them. One of these was free of particle background flares, but the other one was strongly contaminated and only <3 ks of it survived the cleaning process. Details of the X-ray observations are reported in Table 1.

Both of these observations have been processed through the pipeline processing system (Watson et al. 2001), using tasks from the XMM-Newton Science Analysis Software (SAS) v5.1. Subsequent analyses were also performed using the same version of the SAS. All event patterns (single, double and triple) were kept when constructing the event files. This provides maximum sensitivity at high photon energies but the fraction of non-X-ray events rejected is consequently smaller. When flaring intervals are removed from the event lists, higher S/N is usually achieved by keeping all patterns.

The pipeline processing source searching procedure has been adopted. We now sketch briefly its main features. We have used data from EPIC-pn because its sensitivity doubles that of the invidual EPIC-MOS detectors. Images were extracted in the following 4 spectral bands: 0.5-2 keV, 2-4.5 keV, 4.5-7.5 keV and 7.5-10 keV. Exposure maps, which account for vignetting, CCD gaps, bad columns and bad pixels, were constructed for each band. The combination of the 4 images was used to search for sources with an overall likelihood above 16. This corresponds to a probability of a source being spurious of $\sim$ $8\times 10^{-5}$, i.e., up to one spurious detection per image with that likelihood.

First, a simple sliding box algorithm was applied to mask out the brightest sources and to spline-fit the background in each CCD chip. The sliding box algorithm was applied again to search for sources significant against the fitted background. Finally a maximum likelihood fit of the source profiles to the images, simultaneous to all bands, was performed to produce a final source list with exposure corrected count rates in each band. Sources were sorted in terms of the flux in the 0.5-4.5 keV flux. Table 1 lists the countrate to flux conversion factors for both fields which we derived assuming a standard $\Gamma=1.7$ power law absorbed by the galactic column. Fluxes are corrected for galactic absorption. We experimented with variations in the spectral shape of the sources and found changes of up to 15% only in the conversion factor when varying the spectral index from $\Gamma=1.5$ to $\Gamma =2$. That was expected as the 0.5-4.5 keV band was selected because of the fairly flat sensitivity of XMM-Newton accross the whole band. As there are still issues regarding the processing and calibration of EPIC data (out-of-time events, multiple pattern events, etc.), our listed fluxes have to be understood modulo these uncertainties.

 

 

Table 1: Details of XMM-Newton observations.

Target	G133-69 Pos_2	Mkn 205
Observation date	03-07-2000	06-05-2000
XMM-Newton Obsid	0112650501	0124110101
RA(J2000)	01:04:00	12:21:44
DEC(J2000)	-06:42:00	75:18:37
$b (\deg)$	-69.35	+41.67
Clean exposure time (ks)a	15.86	18.97
pn Filter	Thin	Medium
$N_{\rm HI}$	$5.17\times 10^{20}$	$2.81\times 10^{20}$
Conversion factorb	$2.47\times 10^{-12}$	$2.39\times 10^{-12}$

^a This corresponds to the maximum of the exposure map in the pn image.

^b The conversion factor is the ratio between flux in ${\rm erg}\, {\rm cm}^{-2}\, {\rm s}^{-1}$and pn count rate, both in the 0.5-4.5 keV band.

Figure 1: Solid angle surveyed as a function of source flux.

For each 0.5-4.5 keV image we also extracted a sensitivity map (using the SAS task esensmap) showing the minimum count rate that a point source must have to be detectable by the algorithm used, at every position of the detector. We choose a likelihood limit of 10 (as opposed to 16) since we are dealing with a single band. This gives a probability $\sim$ $4.5\times 10^{-5}$ for a spurious detection in a single band (again $\sim$1 spurious detection per image), similar to the multi-band source search. This map takes into account vignetting, inter-CCD gaps and bad pixels and columns. We then computed the total solid angle where a source brighter than any given flux limit would have been detected. In the case of the Mkn 205 we further excluded a circle of radius 2 arcmin around the target. The field also happens to contain an extended source which we identified as the galaxy NGC 4291. The extent of this X-ray source effectively masks out a circle of 1.5 arcmin radius around it where the much enhanced background due to extended X-ray emission prevents us from detecting any further X-ray sources. We therefore included this galaxy as a serendipitous source in our survey but ignored any other possible sources within a circle of 1.5 arcmin radius around it. Figure 1 shows the solid angle surveyed at each flux level. At $2\times 10^{-14}\, {\rm erg}\, {\rm cm}^{-2}\, {\rm s}^{-1}$, which is our survey limit, we have surveyed 0.26 $\deg^2$.

2.2 X-ray sources

The source-searching algorithms produced a number of sources in each field (37 and 52 in the G133-69 Pos_2 and Mkn 205 data respectively), some as faint as $5\times 10^{-15}\, {\rm erg}\, {\rm cm}^{-2}\, {\rm s}^{-1}$(all fluxes refer to the 0.5-4.5 keV band). The faintest of these sources have likelihood detections very close to our threshold. When truncating at a flux of $2\times 10^{-14}\, {\rm erg}\, {\rm cm}^{-2}\, {\rm s}^{-1}$ a total of 12 and 17 X-ray sources were found in the G133-69 Pos_2 and Mkn 205 fields respectively. Two sources in the Mkn 205 field whose positions fall in CCD gaps have already been excluded from the list. The sensivity of both fields was clearly enough to ensure completeness at that flux level, i.e., sources significantly fainter than our survey limit were detected in each field. Care was taken to visually screen the source lists in order to clean it from artifacts derived from the proximity of inter-CCD gaps, bad columns or other cosmetic effects.

Figure 2: Log N-Log S X-ray flux relation for this sample in the 0.5-4.5 keV band (filled circles). For comparison we overlay source counts from ROSAT (continuous curve) from Hasinger et al. (1998) converted with a $\Gamma =2$ spectrum, and from ASCA (Ueda et al. 1999) and Chandra (Mushotzky et al. 2000) in the 2-10 keV band (merged together, dotted curve), converted with a $\Gamma =1.6$ power-law spectrum.

The X-ray source list was then astrometrically corrected. The pipeline-processed data provides astrometry drawn from the attitude and orbit control system (AOCS), which we believe to be good to within a few arcsec. To further improve that, we cross-correlated the source positions of the X-ray sources obtained with a list of optical sources obtained from the i'-band images (see Sect. 3.1) using the SAS task eposcorr. To this goal, we used all detected X-ray sources and all detected optical sources in the field to maximize the number of matches. The situation is summarized in Table 2, were we show that significant astrometric shifts were still present in both data sets. One point that needs stressing is that the number of X-ray to optical matches is much larger when we use the full catalogue of optical sources obtained in our wide-field images than if we used, e.g., the USNO A2 (Monet et al. 1998) catalogued sources. In that case we would be restricted to $\sim$10 matches per field, with the corresponding uncertainty in the astrometric correction parameters. We further discuss the accuracy of the astrometric solution in the X-ray images in Sect. 5.1. Table 3 lists the X-ray sources brighter than our survey limit with the astrometrically corrected positions.

 

 

Table 2: Astrometric correction to pipeline processed XMM-Newton data, derived from cross-correlation with the i'-band optical images.

Field	$\Delta {\rm RA} (\hbox{$^{\prime\prime}$ })$	$\Delta {\rm Dec} (\hbox{$^{\prime\prime}$ })$	Rotation ($\deg$)
Mkn 205	-2.67	+3.09	-0.16
G133-69 Pos_2	-0.73	+0.63	-0.35

In order to gain X-ray spectral information on the X-ray sources, we used the count rates in individual bands to construct the following hardness ratios:

$$HR_1={C(2-4.5\, {\rm keV})-C(0.5-2\, {\rm keV})\over C(2-4.5\, {\rm keV})+C(0.5-2\, {\rm keV})}$$

and

$$HR_2={C(4.5-10\, {\rm keV})-C(2-4.5\, {\rm keV})\over C(4.5-10\, {\rm keV})+C(2-4.5\, {\rm keV})}\cdot$$

Note that these are computed using the exposure-map corrected count-rates, so that energy dependent vignetting is approximately corrected. All sources in the sample selected here had positive count rates in all bands.Also, note that the typical number of counts per source is fairly small and therefore a detailed individual spectral analysis of each source is difficult and beyond the scope of this paper. Table 3 contains the basic X-ray data on these sources.

 

 

Table 3: X-ray sources serendipitously discovered in the XMM-Newton fields under study.

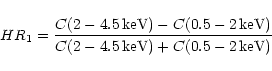
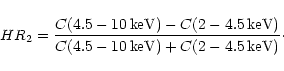
Source name	RA $_{\rm X}^a$ (J2000)	Dec $_{\rm X}^a$ (J2000)	Perrb	Fluxc	HR1	HR2	Comments
XMMU J010316.7-065137	01:03:16.72	-06:51:37.28	1.99	$2.32\pm 0.43$	$-0.62\pm 0.17$	$-0.01\pm 1.00$
XMMU J010327.3-064643	01:03:27.30	-06:46:43.69	0.80	$4.15\pm 0.37$	$-0.15\pm 0.01$	$-0.29\pm 0.37$	Close to pn noisy column
XMMU J010328.7-064633	01:03:28.71	-06:46:33.34	1.30	$2.72\pm 0.31$	$-0.79\pm 0.08$	$+0.09\pm 1.00$	Close to pn noisy column
XMMU J010333.8-064016	01:03:33.86	-06:40:16.07	0.82	$2.65\pm 0.24$	$-0.53\pm 0.08$	$-0.03\pm 0.17$
XMMU J010339.8-065224	01:03:39.87	-06:52:24.74	0.96	$3.73\pm 0.39$	$-0.74\pm 0.08$	$+0.23\pm 0.27$
XMMU J010355.6-063710	01:03:55.62	-06:37:10.48	0.82	$2.56\pm 0.22$	$-0.47\pm 0.08$	$-0.91\pm 1.00$
XMMU J010400.9-064949	01:04:00.96	-06:49:49.37	0.96	$2.70\pm 0.27$	$-0.91\pm 0.09$	$+0.25\pm 1.00$
XMMU J010410.5-063926	01:04:10.56	-06:39:26.46	0.62	$4.17\pm 0.28$	$-0.65\pm 0.05$	$-0.64\pm 0.65$
XMMU J010420.9-064701	01:04:20.91	-06:47:01.46	0.89	$2.39\pm 0.25$	$-0.62\pm 0.09$	$-0.13\pm 0.27$
XMMU J010430.1-064456	01:04:30.13	-06:44:56.07	0.72	$4.90\pm 0.36$	$-0.53\pm 0.06$	$-0.46\pm 0.53$
XMMU J010437.5-064739	01:04:37.56	-06:47:39.29	1.15	$2.29\pm 0.30$	$-0.65\pm 0.12$	$+0.27\pm 0.27$
XMMU J010444.6-064833	01:04:44.68	-06:48:33.42	1.16	$3.96\pm 0.43$	$-0.63\pm 0.09$	$-0.16\pm 0.34$
XMMU J121819.4+751919	12:18:19.48	+75:19:19.61	1.29	$3.17\pm 0.41$	$-0.79\pm 0.02$	$-0.38\pm 1.00$
XMMU J122017.9+752212	12:20:17.98	+75:22:12.17	0.28	$89.6\pm 0.72$	$-0.90\pm 0.01$	$-0.66\pm 0.11$	Extendedd
XMMU J122048.4+751804	12:20:48.43	+75:18:04.10	0.69	$2.97\pm 0.24$	$-0.73\pm 0.02$	$-0.35\pm 0.32$
XMMU J122051.4+752821	12:20:51.45	+75:28:21.84	1.26	$2.07\pm 0.30$	$-0.76\pm 0.03$	$+0.26\pm 0.51$
XMMU J122052.0+750529	12:20:52.02	+75:05:29.44	0.40	$36.0\pm 1.31$	$-0.60\pm 0.01$	$-0.33\pm 0.05$
XMMU J122111.2+751117	12:21:11.29	+75:11:17.19	0.54	$4.12\pm 0.31$	$-0.66\pm 0.01$	$-0.40\pm 0.66$
XMMU J122120.5+751616	12:21:20.56	+75:16:16.10	0.57	$2.98\pm 0.23$	$-0.84\pm 0.01$	$-0.50\pm 0.41$
XMMU J122135.5+750914	12:21:35.59	+75:09:14.28	0.63	$4.99\pm 0.36$	$-0.69\pm 0.02$	$-0.14\pm 0.51$
XMMU J122143.8+752235	12:21:43.88	+75:22:35.32	0.77	$2.20\pm 0.21$	$-0.57\pm 0.04$	$-0.56\pm 0.11$
XMMU J122206.4+752613	12:22:06.48	+75:26:13.78	0.21	$38.4\pm 0.96$	$-0.52\pm 0.01$	$-0.35\pm 0.02$
XMMU J122242.6+751434	12:22:42.69	+75:14:34.96	0.75	$2.15\pm 0.21$	$-0.45\pm 0.05$	$-0.56\pm 0.21$	Close to pn CCD gap
XMMU J122258.1+751934	12:22:58.11	+75:19:34.31	0.55	$5.44\pm 0.36$	$-0.44\pm 0.03$	$-0.49\pm 0.06$	Close to pn CCD gap
XMMU J122318.5+751504	12:23:18.58	+75:15:04.08	0.55	$3.35\pm 0.31$	$-0.72\pm 0.02$	$-0.43\pm 0.42$
XMMU J122344.7+751922	12:23:44.79	+75:19:22.18	0.60	$3.34\pm 0.24$	$-0.74\pm 0.02$	$-0.82\pm 0.28$
XMMU J122351.0+752227	12:23:51.02	+75:22:27.99	0.36	$11.6\pm 0.56$	$-0.62\pm 0.01$	$-0.44\pm 0.05$
XMMU J122435.7+750812	12:24:35.77	+75:08:12.02	1.36	$2.10\pm 0.37$	$-0.77\pm 0.04$	$-0.20\pm 1.00$
XMMU J122445.5+752224	12:24:45.53	+75:22:24.80	0.88	$4.16\pm 0.42$	$-0.77\pm 0.02$	$-0.31\pm 0.73$

Notes to Table: ^a Position of the X-ray source after astrometric correction; ^b Position error in arcsec (statistical only); ^cFlux in the 0.5-4.5 keV band in units of $10^{-14}\, {\rm erg}\, {\rm cm}^{-2}\, {\rm s}^{-1}$; ^d The flux for this source has been estimated from aperture photometry.

In Fig. 2 we plot the integrated source counts derived from this survey. The source density at the survey limit is $113\pm 21$ sources $\deg^{-2}$. This curve is to be compared with the ROSATsource counts (Hasinger et al. 1998) which we converted to our 0.5-4.5 keV band by using a $\Gamma =2$ spectrum which is consistent with the average value of HR₁ (see below). Our source counts are $\sim$$60\%$ higher than the ROSAT ones at the survey limit. Choosing a conversion factor corresponding to a power-law with spectral index $\Gamma=1.7$ just brings the ROSAT curve up by $\sim$$15\%$, still significantly below our source counts.

We also compare the source counts with those derived in the 2-10 keV from ASCA (Ueda et al. 1999) and Chandra (Mushotzky et al. 2000). Note that the Baldi et al. (2001) source counts, based on XMM-Newton data, are consistent with these earlier work. Here a conversion factor for $\Gamma =1.6$ has been applied, which is consistent with the value of HR₂ (see below). Our source counts fall modestly below (17%, only $\sim$1 sigma significant) those in the harder band at the survey limit. It is clear that by selecting in the 0.5-4.5 keV band we find a large fraction of the sources that ROSAT missed, but we may still be missing a small fraction of the hard sources detected in the 2-10 keV band.

Figure 3 shows the hardness ratios for the sources as a function of flux. We must caution that although the two fields under consideration have different Galactic absorbing columns and furthermore have been observed with different EPIC-pn filters (thin and medium, see Table 1), the effect of both of these facts on the hardness ratios (particularly HR₁) is completely negligible. No obvious trend of the source spectra is seen with source flux. The so-called spectral paradox (Fabian & Barcons 1992), i.e., the source's spectra being steeper than the X-ray background spectrum ( $\Gamma\sim 1.4$), is therefore not obviously solved at this flux level, i.e., we do not find a significant sample of sources that have an X-ray spectrum close to that of the X-ray background. This is also revealed by the histograms of HR₁ and HR₂ which are shown in Fig. 4 together with the expected values for various power laws with galactic absorption. The weighted averages of the hardness ratios are $\langle HR_1\rangle=-0.69\pm 0.03$ and $\langle HR_2\rangle=-0.37 \pm 0.03$, consistent with a fairly steep X-ray spectrum ($\Gamma=$ 1.6-2.0). Further details on the X-ray spectra of the different source classes are given in Sect. 5.2.

Figure 3: Hardness ratios HR1 and HR2 as a function of X-ray flux. Symbols are as follows: filled dots are BLAGNs, empty circles are NELGs, triangles are Galaxies, asterisks are AC and crosses are non-identified sources. We also overlay expected values of HR1 and HR2 for single power-law spectra with $\Gamma~=~2$ and $\Gamma =1.4$.

Figure 4: Histograms of the values of HR1 and HR2. Marks for standard power-law spectra with various values of the photon spectral index $\Gamma$ are shown.