

Up: A photometric-dynamic model to
Subsections
- 1.
- Image of comet Hale-Bopp on 10 April, 1997 in R filter
obtained from the Vainu Bappu observatory was used to investigate the
intensity variations in the shells and the coma.
- 2.
- Published polarizations on 10 June, 1996, 30 September, 1996,
and 9th April, 1997 separately in the coma and bright regions
by Hadamcik et al. (1997) were used to
investigate the nature of the grains in the coma.
- 3.
- As the colour of the grains do not change drastically with phase angle,
we set a conservative limit of
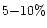 per 1000 Å on the
shells and
per 1000 Å on the
shells and
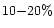 per 1000 Å on the regions between the shells representing
the coma based on the colour reported by
Bellucci (1998),
Furusho et al. (1999),
Kiselev & Velichko (1997) and
Kolokolova et al. (2001).
per 1000 Å on the regions between the shells representing
the coma based on the colour reported by
Bellucci (1998),
Furusho et al. (1999),
Kiselev & Velichko (1997) and
Kolokolova et al. (2001).
- 4.
- Published aperture polarimetric observations at a range of
phase angles by several groups (Sect. 1 and references therein).
Cometary grains are known to be porous and contain an organic component
(Greenberg & Hage 1990; Hage & Greenberg 1990;
Krishnaswamy et al. 1988; Xing & Hanner 1997).
The dynamics as well as the scattering properties of the grains are
affected by porosity and organic content, as both these factors
modify the complex refractive indices of the grains significantly.
The silicaceous components in the grain have been identified from
their emission signatures in the IR spectra in the
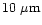 region by Hayward et al. (2000) and
Wooden et al. (1999). In the visible and near IR regions,
it is futile to identify the Mg rich
silicates either in glassy or crystalline form in the composite
grains using their
scattered radiation, as presence of
even a small amount of organic content of 1/12 by weight
will be sufficient to significantly
alter the refractive index of the composite grain.
Hence silicates were sub grouped
into three classes depending on the absorption index k:
region by Hayward et al. (2000) and
Wooden et al. (1999). In the visible and near IR regions,
it is futile to identify the Mg rich
silicates either in glassy or crystalline form in the composite
grains using their
scattered radiation, as presence of
even a small amount of organic content of 1/12 by weight
will be sufficient to significantly
alter the refractive index of the composite grain.
Hence silicates were sub grouped
into three classes depending on the absorption index k:
- 1.
- Mg rich silicates with
0.0001<k<0.001, we
refer to this group as SiX.
Forsterite, with the optical constants by Scott & Duley (1996)
was taken as the sample representative of this class (class 1).
- 2.
- Astronomical
silicate (Draine 1985; Draine & Lee 1984)
with
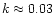 (SiA). The present study uses
the constants of crystalline olivine constructed by Li & Greenberg (1997)
which uses the absorptive index of SiA in the visible region.
Since polarization mainly depends on the
absorptive index, we refer to this sample also as SiA (class 2).
(SiA). The present study uses
the constants of crystalline olivine constructed by Li & Greenberg (1997)
which uses the absorptive index of SiA in the visible region.
Since polarization mainly depends on the
absorptive index, we refer to this sample also as SiA (class 2).
- 3.
- Mg poor silicates characterized by an absorption at wavelengths
shortward of 0.5
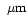 and with k > 0.03. Amorphous olivine (Aol)
and pyroxene (Apy)
with Mg number of 0.5 (Dorschner et al. 1995) were taken as
representatives of this class (class 3).
and with k > 0.03. Amorphous olivine (Aol)
and pyroxene (Apy)
with Mg number of 0.5 (Dorschner et al. 1995) were taken as
representatives of this class (class 3).
At
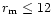 ,
distinction between
SiA and SiX almost vanishes.
Following Li & Greenberg (1998), the organic refractory component was
assumed to be a composite of interstellar refractory (Li & Greenberg 1997)
and amorphous carbon (Rouleau & Martin 1991) of equal mass.
Effective refractive indices of the composite grains were determined using
Bruggmann's mixing rule.
Collections of individual grains of these silicates
with the organic refractory component in the mass ratios
,
distinction between
SiA and SiX almost vanishes.
Following Li & Greenberg (1998), the organic refractory component was
assumed to be a composite of interstellar refractory (Li & Greenberg 1997)
and amorphous carbon (Rouleau & Martin 1991) of equal mass.
Effective refractive indices of the composite grains were determined using
Bruggmann's mixing rule.
Collections of individual grains of these silicates
with the organic refractory component in the mass ratios
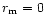 ,
1, 2, 8, 12 and
,
1, 2, 8, 12 and 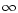 and
the porosities
and
the porosities 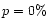 ,
,
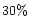 ,
,
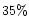 ,
,
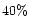 ,
,
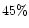 ,
,
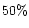 ,
,
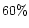 ,
,
 ,
,
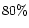 and
and 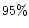 were considered.
were considered.
Phase dependence of polarization carries valuable information on the
interaction between the reflected and refracted components from the grain
along different scattering directions. The fraction of the refracted component
depends on
the optical properties of the grain, its size and shape.
Polarization of light scattered by an ensemble of spherical grains at the three
continuum
wavelengths 0.6840 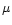 m, 0.4845
m, 0.4845 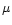 m and
0.3650
m and
0.3650 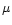 m corresponding to aperture polarimetry observations by
Ganesh et al. (1998) and Manset & Bastien (1998) were
computed.
For a proper match with these observations over the entire range of
phase angles, combinations of grain types and
proper choice of their size distribution are essential.
Hanner size distribution (Hanner 1985)
m corresponding to aperture polarimetry observations by
Ganesh et al. (1998) and Manset & Bastien (1998) were
computed.
For a proper match with these observations over the entire range of
phase angles, combinations of grain types and
proper choice of their size distribution are essential.
Hanner size distribution (Hanner 1985)
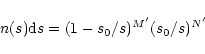 |
(20) |
was used.
The constants s0,
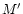 and
and
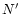 determine the
slopes at the lower and upper size domains and the
radius
determine the
slopes at the lower and upper size domains and the
radius 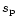 at which n(s) is maximum.
As a first guess, four component equal weight
inter-combinations of the three classes of silicates, each with 30 different combinations of p and
at which n(s) is maximum.
As a first guess, four component equal weight
inter-combinations of the three classes of silicates, each with 30 different combinations of p and 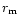 were considered.
A total of
810000 combinations were compared in the least square sense
with the observed phase curves of Ganesh et al. (1998).
The size distribution parameters were varied to improve the
were considered.
A total of
810000 combinations were compared in the least square sense
with the observed phase curves of Ganesh et al. (1998).
The size distribution parameters were varied to improve the 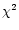 values.
The constants in set 'a' in Table 1 yielded best fit.
values.
The constants in set 'a' in Table 1 yielded best fit.
The intensity contribution
I(s)n(s)ds for this distribution at a mean wavelength of
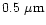 is shown as the solid line in Fig. 2.
is shown as the solid line in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f2.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg174.gif) |
Figure 2:
Intensity contribution of grains of sizes between
s and
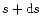 ,
along the scattering
angle of ,
along the scattering
angle of  and at a wavelength of
and at a wavelength of
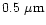 for the
size distribution constants in Table 1. All the three curves have been normalized
to enable a direct comparison. The solid vertical line indicates the lower limit
of 0.05
for the
size distribution constants in Table 1. All the three curves have been normalized
to enable a direct comparison. The solid vertical line indicates the lower limit
of 0.05
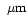 on the grain size used in the present investigation.
on the grain size used in the present investigation. |
Table 2 gives the grain types which were common in the first 100 best fitting
combinations.
It is striking to note that except for the highly porous grains,
all grain types have porosities in the range between 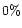 (compact)
and
(compact)
and 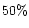 .
.
The size distribution
'a' represents the combined grain population in the coma and shell
which are sampled in the aperture of
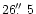 .
In the present work it is attempted to investigate
the relative fraction
of the grain type and their size distributions
separately in the coma and the shells.
.
In the present work it is attempted to investigate
the relative fraction
of the grain type and their size distributions
separately in the coma and the shells.
The simulations of the intensity, colour and polarization maps
of comet Hale-Bopp were carried out for
the geometry on 10 April, 1997, in the
wavelength band corresponding to the cometary continuum wavelengths
at
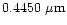 and
and
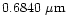 for the grain types in Table 2.
The pole positions and latitude of the
sources are adapted from Paper II.
The grain velocities computed using Eq. (2)
with
v0 = 0.63 kms-1 were found to be within
for the grain types in Table 2.
The pole positions and latitude of the
sources are adapted from Paper II.
The grain velocities computed using Eq. (2)
with
v0 = 0.63 kms-1 were found to be within
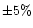 -
-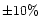 to the values computed using Eq. (1). The latter was used
in the simulations.
The coma was simulated by considering emission from a grid on the
comet at intervals of
to the values computed using Eq. (1). The latter was used
in the simulations.
The coma was simulated by considering emission from a grid on the
comet at intervals of 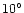 in latitude and
in latitude and
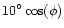 in longitude,
where
in longitude,
where 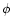 is the latitude of the point on the grid.
The sources are assumed to be active when sunlit.
The trajectories
of the dust grains are computed assuming collimated emissions. In
reality, the emission may be spread over a cone. Further, the velocity
of the grains will have a spread due to deviation from their assumed
sphericity, finite size of the active
regions and possible irregular local terrain. Their cumulative effect
will produce a broadening of the shells. As it is difficult to model each
of these effects, the sky plane position of the grains
were convolved
with a Gaussian-random profile with a sigma of 1
is the latitude of the point on the grid.
The sources are assumed to be active when sunlit.
The trajectories
of the dust grains are computed assuming collimated emissions. In
reality, the emission may be spread over a cone. Further, the velocity
of the grains will have a spread due to deviation from their assumed
sphericity, finite size of the active
regions and possible irregular local terrain. Their cumulative effect
will produce a broadening of the shells. As it is difficult to model each
of these effects, the sky plane position of the grains
were convolved
with a Gaussian-random profile with a sigma of 1
 5.
To include the effect of spreading with time,
the sigma was allowed to increase by 0
5.
To include the effect of spreading with time,
the sigma was allowed to increase by 0
 25 per day.
Due to rotation of the nucleus, grains in the expanding jets are swept
along the azimuth of the comet giving the appearance of a set of shells,
one shell per rotation.
The simulated images contain 8 shells and coma
dust ejected between 0 - 150 hr.
25 per day.
Due to rotation of the nucleus, grains in the expanding jets are swept
along the azimuth of the comet giving the appearance of a set of shells,
one shell per rotation.
The simulated images contain 8 shells and coma
dust ejected between 0 - 150 hr.
Larger grains in the coma compared to the shells
or a different grain composition for the two regions
have been inferred by
Hadamcik et al. (1997),
Jockers et al. (1997) and
Tanga et al. (1997).
High polarization
and high silicate IR emission (Sect. 1 and references therein) in the shells
suggest predominance of smaller grains in these regions.
The size distribution 'a' obtained by overall fit to coma and
the shells may represent a distribution which is the average
of a larger grain population for the coma and finer grains in the shells.
The simulations were carried out for the distribution
'b' (Table 1),
used by Hayward et al. (2000) to include
larger grains. The dot dashed line in Fig. 2 shows this distribution.
The size distribution of the smaller set of grains should be such that
the total ensemble should
produce the observed trend of
increase of polarization with wavelength.
As shown in the next section, the distribution 'c' with the coefficients
given in Table 1 and the intensity distribution curve shown as
the "dashed'' line in Fig. 2 produces this trend.
Effects of variation of porosity, organic fraction and size distributions
are demonstrated in the left, middle and right columns of Fig. 3 for
distributions 'c',
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ms8445f3.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg186.gif) |
Figure 3:
Effects of grain size distribution ('c': left, 'a': middle,
'b': right) and organic content
on the spatial
variation of intensity (lower panel, superposed on the observations), colour (middle panel),
polarizations 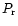 and
and 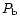 ( solid and dashed lines in top panel),
across the coma
along the sunward - anti sunward direction for the geometry on April 10, 1997.
The horizontal line at
( solid and dashed lines in top panel),
across the coma
along the sunward - anti sunward direction for the geometry on April 10, 1997.
The horizontal line at 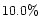 polarization represents
polarization represents 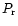 in the dark regions
(Hadamcik et al. 1997). The lower horizontal
line at in the dark regions
(Hadamcik et al. 1997). The lower horizontal
line at 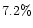 represents the expected value of
represents the expected value of 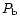 . . |
'a' and 'b' respectively
for a few sample grain types in Table 2.
Variation of intensity, colour and polarizations
along the solar - anti-solar direction across
the simulated comae are shown in the
lower, middle and top sections respectively. For distribution 'c',
at porosities less than 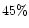 ,
the polarization in
,
the polarization in
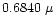 ,
,
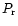 (solid line) is larger compared to
that in
(solid line) is larger compared to
that in
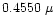 ,
,
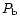 (dashed line).
The horizontal line at
(dashed line).
The horizontal line at 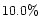 polarization level indicates
the reported value in dark regions by
Hadamcik et al. (1997) in red. The lower horizontal
line at
polarization level indicates
the reported value in dark regions by
Hadamcik et al. (1997) in red. The lower horizontal
line at 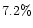 is the expected polarization in
is the expected polarization in
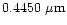 based on the
based on the
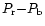 values from published
aperture photometry.
The error bars in the observed intensity cuts represent the uncertainty in the determination of sky
background which is the largest source of error in the image.
The upper and
lower limits correspond to sky fluxes which were
values from published
aperture photometry.
The error bars in the observed intensity cuts represent the uncertainty in the determination of sky
background which is the largest source of error in the image.
The upper and
lower limits correspond to sky fluxes which were 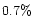 and
and 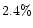 of
the central flux. The solid curve in the middle section of this panel shows the
simulated colour variation.
The steep fall in intensity
and polarization beyond
of
the central flux. The solid curve in the middle section of this panel shows the
simulated colour variation.
The steep fall in intensity
and polarization beyond 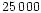 km on the sunward side
in the coma of grains with
km on the sunward side
in the coma of grains with
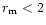 and distributions 'a' and 'c'
occurs because of their large
and distributions 'a' and 'c'
occurs because of their large  (Eqs. (4) and (5)) values.
The increase in
polarization beyond
(Eqs. (4) and (5)) values.
The increase in
polarization beyond 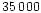 km in the sunward direction has opposite polarization colour
as this is caused by the larger grains in the tail end of distribution.
km in the sunward direction has opposite polarization colour
as this is caused by the larger grains in the tail end of distribution.
Figure 3 illustrates clearly the effect of size distribution
on the colour and polarization. For grains of medium porosity (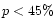 ),
),
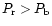 for distribution 'c',
for distribution 'c',
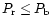 for 'a' and
for 'a' and
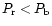 for 'b'. The anti-correlation in colour and polarization
as pointed out by Kolokolova et al. (2001)
is clearly noticeable for 'a' and 'b': the collection
'b' (right) which has larger grains has lower polarization but larger colour
than the distribution 'a' (middle). Contrary to scattering behavior of
sub-micron sized grains,
the absorptive grains in population 'c' are redder compared to that in 'a'which contains additional larger grains. The reddening is found to increase
with the refractive index of the grain either due to increase of organic
fraction or reduction in porosity. It is marginally higher for Aol
compared to the less absorptive SiA. As pointed out by
Kolokolova et al. (2001), a grain may be redder if its
size parameter x is just beyond the scattering peak. The scattering peak
occurs at
for 'b'. The anti-correlation in colour and polarization
as pointed out by Kolokolova et al. (2001)
is clearly noticeable for 'a' and 'b': the collection
'b' (right) which has larger grains has lower polarization but larger colour
than the distribution 'a' (middle). Contrary to scattering behavior of
sub-micron sized grains,
the absorptive grains in population 'c' are redder compared to that in 'a'which contains additional larger grains. The reddening is found to increase
with the refractive index of the grain either due to increase of organic
fraction or reduction in porosity. It is marginally higher for Aol
compared to the less absorptive SiA. As pointed out by
Kolokolova et al. (2001), a grain may be redder if its
size parameter x is just beyond the scattering peak. The scattering peak
occurs at
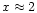 for absorptive grains with
an effective refractive index of
for absorptive grains with
an effective refractive index of 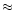
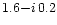 corresponding to
corresponding to
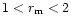 and
and
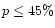 .
For less absorptive grains of pure silicates
of effective refractive index
.
For less absorptive grains of pure silicates
of effective refractive index 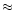
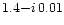 corresponding to
corresponding to
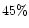 porosity,
the peak occurs
at
porosity,
the peak occurs
at
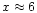 (Wickramasinghe 1973).
For the average grain size of
(Wickramasinghe 1973).
For the average grain size of
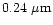 at the broad peak in Fig. 2
for distribution 'c', the size parameters at
at the broad peak in Fig. 2
for distribution 'c', the size parameters at
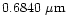 and
and
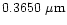 are 2.2 and 4.4 respectively. This range in size parameter is beyond the
scattering peak for absorptive grains and before for the pure silicates.
This explains the red colour of the absorptive grains and the blue colour
of the less absorptive ones.
Further, for this distribution
are 2.2 and 4.4 respectively. This range in size parameter is beyond the
scattering peak for absorptive grains and before for the pure silicates.
This explains the red colour of the absorptive grains and the blue colour
of the less absorptive ones.
Further, for this distribution
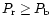 ,
the reason for this large polarization colour is that
in this domain of
,
the reason for this large polarization colour is that
in this domain of
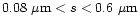 ,
the grain becomes increasingly forward
scattering with
increase in its size parameter.
Blue light is therefore more forward scattered than the red. With increase in the transmitted
part of blue light
which is parallelly polarized (negative polarization) the resultant
polarization is lower compared to that in red.
On the other hand, for the large grain population 'b',
,
the grain becomes increasingly forward
scattering with
increase in its size parameter.
Blue light is therefore more forward scattered than the red. With increase in the transmitted
part of blue light
which is parallelly polarized (negative polarization) the resultant
polarization is lower compared to that in red.
On the other hand, for the large grain population 'b',
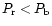 ,
which is opposite to the observed trend for comets. Therefore, the difference
in the grain populations in the coma and shells may in most part be due to difference
in the silicate to organic ratio rather than difference in grain sizes.
,
which is opposite to the observed trend for comets. Therefore, the difference
in the grain populations in the coma and shells may in most part be due to difference
in the silicate to organic ratio rather than difference in grain sizes.
The selected
grain types should also explain the phase dependent polarization in
various colours.
Figure 4 shows the phase dependence of the polarization produced by the same
grain types as in Fig. 3
at seven continuum wavelengths
for distributions c (left),
![\begin{figure}
\par\includegraphics[width=15cm,clip]{ms8445f4.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg207.gif) |
Figure 4:
Effects of grain size distribution and organic content
on the phase dependence of polarization for the same
sample grain types as in Fig. 3. Details of the computed curves and the data are same as for
Fig. 6. |
a (middle) and b (right) respectively.
The polarizations
at
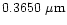 (short dashed line),
(short dashed line),
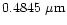 (dotted line),
(dotted line),
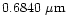 (solid line),
(solid line),
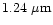 (short dash - dot),
(short dash - dot),
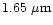 (short dash - dot, thick line)
and
(short dash - dot, thick line)
and
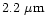 (short dash - long dash) show different trends for the three
distributions. The observed polarizations in the optical by
Ganesh et al. (1998), Hadamcik et al. (1997),
Kiselev & Velichko (1997) and Manset & Bastien (1998)
and the infrared observations by Hasegawa (1999)
are over plotted.
The phase dependence and colour of polarization again critically depend
on the size distribution. The relative polarization colour
represented by (
(short dash - long dash) show different trends for the three
distributions. The observed polarizations in the optical by
Ganesh et al. (1998), Hadamcik et al. (1997),
Kiselev & Velichko (1997) and Manset & Bastien (1998)
and the infrared observations by Hasegawa (1999)
are over plotted.
The phase dependence and colour of polarization again critically depend
on the size distribution. The relative polarization colour
represented by (
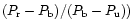 matches with the observed
ratio for grains of distribution 'c' with
matches with the observed
ratio for grains of distribution 'c' with
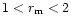 and
and 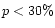 ,
where
,
where 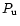 is polarization in
is polarization in
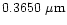 .
Organic refractory component has increased absorption in blue and UV.
Comparing SiA grains of
.
Organic refractory component has increased absorption in blue and UV.
Comparing SiA grains of 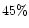 porosity of
porosity of
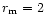 (SiA0245) and
(SiA0245) and
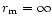 (SiA
(SiA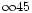 ), in this grain size domain,
polarizations in
), in this grain size domain,
polarizations in
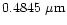 and 0.3650 are therefore lower in the latter compared to the former
because of lesser attenuation of the refracted component.
Grains of Aol
and 0.3650 are therefore lower in the latter compared to the former
because of lesser attenuation of the refracted component.
Grains of Aol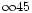 show their characteristic signature. The absorption
in blue causes higher positive polarization in all size domains.
The fluctuations in the large pure silicate grains are caused by the interference
between the refracted and reflected components of light (Kolokolova et al.
1997).
show their characteristic signature. The absorption
in blue causes higher positive polarization in all size domains.
The fluctuations in the large pure silicate grains are caused by the interference
between the refracted and reflected components of light (Kolokolova et al.
1997).
Figures 3 and 4 clearly demonstrate that porosity, organic fraction and
the size distribution of grains in the coma and shells
play an important role in controlling the phase dependence of polarization,
colour of polarization, photometric colour and spatial variation
of intensity in a comet. We exploit this to investigate the
composition of grains in the coma and shell separately.
Synthetic comae were constructed by combining the grain types in
Table 2.
The relative weights were adjusted to fulfill the following four observational
constrains:
- 1.
- The published values of red polarization between the shells (dark regions)
of
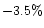 ,
,
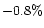 and
and 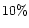 at phase angles of
at phase angles of
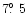 ,
,
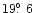 and
and
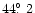 respectively by Hadamcik et al. (1997),
and blue polarizations
deduced from the published aperture photometry;
respectively by Hadamcik et al. (1997),
and blue polarizations
deduced from the published aperture photometry;
- 2.
- Colour of the coma in the range
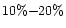 ;
;
- 3.
- Higher polarization on the anti-sunward direction.
All the three size distributions were considered for each grain type.
The weights and the size distributions which met this test are given in
Table 3.
These
weights correspond to the relative contribution to the red intensity rather
than the number of grains.
Thus the coma may contain a large fraction of grains with distribution 'c'.
However such grains will produce a very flattened coma. Hence these grains
may be part of larger fluffy grains some of which may also be
physically associated with grains of distribution 'b'. The dynamics will then
be controlled by an average value of  and the coma profile will
follow the observed coma (regions between
the shells). Alternatively, some of the grains may
have distributed sources and hence have a synthetic radial
profile mimicking the grains of distribution 'b'.
and the coma profile will
follow the observed coma (regions between
the shells). Alternatively, some of the grains may
have distributed sources and hence have a synthetic radial
profile mimicking the grains of distribution 'b'.
The weights of the grain types in the shells were adjusted so that the
simulated shells have the following attributes reported by
Hadamcik et al. (1997),
Jockers et al. (1997) and Tanga et al. (1997):
- 1.
- High polarization on the shells;
- 2.
- Bluer colour of the shells by
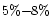 ;
;
- 3.
- Rapid decline of polarization of the shells on the
sunward side;
- 4.
- Intensity contrast between the shells and the underlying coma.
Figure 5 shows the simulations of shells
made up of grain types which produce polarizations larger than the published
aperture polarization measurements.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{ms8445f5.eps} .\end{figure}](/articles/aa/full/2002/04/aa8445/Timg237.gif) |
Figure 5:
Column 1: observed processed image from VBO  (projected
cometocentric distance)-1.
North is top and East is left.
The sets of shells expanding from the nucleus in the direction of N-W, S-W and
S-E are from the sources at
(projected
cometocentric distance)-1.
North is top and East is left.
The sets of shells expanding from the nucleus in the direction of N-W, S-W and
S-E are from the sources at 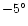 , ,
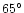 and
and 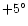 respectively.
Columns 2 and 3: simulated intensity (shell) and polarization (shell + coma) maps.
Column 4: intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel),
respectively.
Columns 2 and 3: simulated intensity (shell) and polarization (shell + coma) maps.
Column 4: intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel), 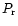 (solid line in top panel),
(solid line in top panel),
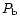 (short dashed line in top panel) and
(short dashed line in top panel) and
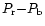 (long dashed line in
top panel).
(long dashed line in
top panel). |
The first column shows the observed processed image from VBO.
The shell structures are enhanced by
dividing by a synthetic image of a coma (Chakraborty 2001) in which
the intensity declines
as the inverse of projected cometocentric distance. The coma image was
scaled so that the resultant normalized flux
in the N-E edge of the image which is devoid of shells, was unity.
The sets of shells expanding from the nucleus in the direction of N-W, S-W and
S-E are from the sources at 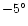 ,
,
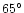 and
and 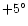 respectively (Papers I and II).
The simulated intensity map of the shells and polarization map of the
shells superposed on the coma are shown in second
and third columns respectively.
Each simulated image is divided into
respectively (Papers I and II).
The simulated intensity map of the shells and polarization map of the
shells superposed on the coma are shown in second
and third columns respectively.
Each simulated image is divided into
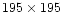 square pixels of
size 0
square pixels of
size 0
 5 on a side.
The number density of the grains in the jets were adjusted to
match the intensity variation in the shells.
The fourth column shows the intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel),
5 on a side.
The number density of the grains in the jets were adjusted to
match the intensity variation in the shells.
The fourth column shows the intensity scans of the shells superposed on the
coma (lower panel), colour in % (middle panel), 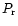 (solid line in top panel),
(solid line in top panel),
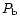 (short dashed line in top panel)
and
(short dashed line in top panel)
and
 (long dashed line in
top panel).
Each grain type has its
characteristic signature in the intensity, colour and polarization map.
(long dashed line in
top panel).
Each grain type has its
characteristic signature in the intensity, colour and polarization map.
- 1.
- Row 1 (starting from below):
grains of the type "Si
 45'' with distribution 'a'produce shells that resemble the observed ones. The shells are bluer
but the polarization is only marginally higher than the ambient coma.
45'' with distribution 'a'produce shells that resemble the observed ones. The shells are bluer
but the polarization is only marginally higher than the ambient coma.
- 2.
- Row 2:
grains of the type "Si
 45'' but with distribution 'c'appear to be likely candidate as
45'' but with distribution 'c'appear to be likely candidate as  is larger on the shell compared to coma.
However neither is there a rapid fall in polarization in the sun ward
direction nor an increase in polarization in the anti sunward direction.
is larger on the shell compared to coma.
However neither is there a rapid fall in polarization in the sun ward
direction nor an increase in polarization in the anti sunward direction.
- 3.
- Row 3 & 4:
increasing the organic fraction to
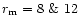 causes the older shells
to be depleted of finer grains as these are blown away towards the
anti-sunward direction. The shells are compressed and
a piling up of shells older than four rotations causes a "shell pause''
like structure in the polarization map and
an abrupt decline in polarization. In the intensity map, the pile up of matter
merges with the coma. This region appears bluer in the colour map because of
the shell material. For a detailed comparison with observed colour and
polarization maps, shells ejected over a larger numbers of the nuclear rotations
(>8) and coma ejections over an extended duration (t > 150 hr)
are required.
causes the older shells
to be depleted of finer grains as these are blown away towards the
anti-sunward direction. The shells are compressed and
a piling up of shells older than four rotations causes a "shell pause''
like structure in the polarization map and
an abrupt decline in polarization. In the intensity map, the pile up of matter
merges with the coma. This region appears bluer in the colour map because of
the shell material. For a detailed comparison with observed colour and
polarization maps, shells ejected over a larger numbers of the nuclear rotations
(>8) and coma ejections over an extended duration (t > 150 hr)
are required.
- 4.
- Row 5 & 6:
with increase in the organic fraction to
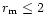 ,
the radiation pressure
blows out grains from the shells older than two rotations and produces
a very steep increase in polarization in the anti-sunward direction and
an abrupt fall in the sunward direction.
The contrast in colour between the coma and the shells disappears
The effect is pronounced for
,
the radiation pressure
blows out grains from the shells older than two rotations and produces
a very steep increase in polarization in the anti-sunward direction and
an abrupt fall in the sunward direction.
The contrast in colour between the coma and the shells disappears
The effect is pronounced for
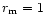 .
.
- 5.
- Row 7: porous grains are known to produce
large polarizations. Hence we considered a collection of highly porous
grains
with distribution 'a' which are assumed to be homogeneous in the
Rayleigh limit. This set produces well constrained
shells which survive several rotation periods.
This is because of
lower
 values which vary slowly with the grain size.
Although the present approach of EMT + Mie theory
is known to have serious limitations for porous grains,
these simulations help to visualize the signature of highly porous homogeneous
grains.
The streaks in the polarization map streaming away in the anti-sun direction represent
the small grains in the population.
values which vary slowly with the grain size.
Although the present approach of EMT + Mie theory
is known to have serious limitations for porous grains,
these simulations help to visualize the signature of highly porous homogeneous
grains.
The streaks in the polarization map streaming away in the anti-sun direction represent
the small grains in the population.
From Fig. 5, it is apparent that larger polarization and bluer colour
on the shells are produced by grains of SiA with
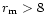 .
However, not more than 3 shells survive the radiation pressure forces while
the observed image after careful evaluation and removal of the
underlying coma
shows up to 8 shells (Chakraborty 2001). Therefore a population
of grains with high polarization but low
.
However, not more than 3 shells survive the radiation pressure forces while
the observed image after careful evaluation and removal of the
underlying coma
shows up to 8 shells (Chakraborty 2001). Therefore a population
of grains with high polarization but low  ,
similar to the over simplified
example of a uniform porous grain in Row 7 in Fig. 5 also appear to be
needed to explain the survival of older shells.
A reliable estimate of the fractional weights of these grain types can
only be made by a quantitative comparison of the polarization maps.
In the absence of availability of such a data set, we make use of the
aperture polarimetry observations.
As the aperture photometry represents combined contribution of coma and shells,
the grains which may explain the polarization
on the shell, when added in the same proportion to the selected
combination representing the coma should explain
the aperture polarimetric data. The best fitting weights for the shells
which fitted polarization vs. phase curves
are given in Table 3. Figure 6 shows the resultant simulated polarization vs. phase
curves.
,
similar to the over simplified
example of a uniform porous grain in Row 7 in Fig. 5 also appear to be
needed to explain the survival of older shells.
A reliable estimate of the fractional weights of these grain types can
only be made by a quantitative comparison of the polarization maps.
In the absence of availability of such a data set, we make use of the
aperture polarimetry observations.
As the aperture photometry represents combined contribution of coma and shells,
the grains which may explain the polarization
on the shell, when added in the same proportion to the selected
combination representing the coma should explain
the aperture polarimetric data. The best fitting weights for the shells
which fitted polarization vs. phase curves
are given in Table 3. Figure 6 shows the resultant simulated polarization vs. phase
curves.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{ms8445f6.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg244.gif) |
Figure 6:
Fitted polarization vs. phase angle curves for comet Hale-Bopp:
computed curves:
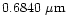 (solid line),
(solid line),
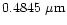 (dotted line),
(dotted line),
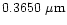 (dashed line),
(dashed line),
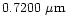 (long
dashed line),
(long
dashed line),
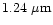 (short dash - dot, thin line),
(short dash - dot, thin line),
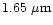 (short dash - dot, thick line) and
(short dash - dot, thick line) and
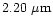 (long dash - short dash).
(long dash - short dash). |
At phase angles larger than 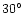 ,
the fits were better if the relative
fraction of Mg poor silicate grains
with distribution b were increased gradually with heliocentric distance.
A possible explanation for this is given in Sect. 6.
,
the fits were better if the relative
fraction of Mg poor silicate grains
with distribution b were increased gradually with heliocentric distance.
A possible explanation for this is given in Sect. 6.
The resultant simulated intensity maps of the shells and polarization maps of
shells and coma using weights in Table 3 are shown in the top, middle and right
panels of Fig. 7.
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{ms8445f7.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg246.gif) |
Figure 7:
Top left: the processed observed image as in Fig. 5.
Top middle and right: simulated intensity maps of the shells and
polarization maps of
shells+coma using weights in Table 3.
The lower panel shows
the intensity, colour and polarization scans
in the sun-ward - anti-sun-ward direction. |
The first
panel is the processed observed image as in Fig. 5.
Separation of the high  (
(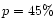 )
grains and low
)
grains and low  grains
(
grains
(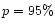 )
components produces the splitting of the shells in the N-W and S-E
region of the simulated image (Table 3).
)
components produces the splitting of the shells in the N-W and S-E
region of the simulated image (Table 3).
The lower panel of Fig. 7 shows
the intensity, colour and polarization scans
in the sunward - anti-sunward direction.
In order to reduce the fluctuations arising due to discretization of
cometary longitudes and latitudes, the scans
have been averaged over 9 pixels (
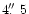 ). The polarization
contrast between the coma and the shells are therefore reduced in these plots.
The maximum and minimum value of polarization in the map however correspond to
). The polarization
contrast between the coma and the shells are therefore reduced in these plots.
The maximum and minimum value of polarization in the map however correspond to
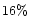 in the bright regions and
in the bright regions and 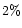 beyond the 4th shell in the sunward
direction.
beyond the 4th shell in the sunward
direction.
The width
and separation of the shells depend
on the pole position,
velocity
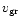 and the acceleration
and the acceleration 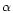 of the grains.
The later two quantities depend on the size distribution and the nature
of the grains.
For the geometry on 10 April, 1997, the uncertainty
in the computed separation of the shells from the source at
of the grains.
The later two quantities depend on the size distribution and the nature
of the grains.
For the geometry on 10 April, 1997, the uncertainty
in the computed separation of the shells from the source at 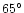 ,
is found to be
,
is found to be
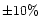 along the projected sunward direction for a change in
along the projected sunward direction for a change in
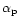 by
by
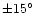 and
and
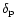 by
by
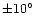 .
The model thus reproduces the shells
within an accuracy of
.
The model thus reproduces the shells
within an accuracy of 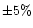 in the shell separation corresponding
to the uncertainty of
in the shell separation corresponding
to the uncertainty of
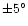 in
the pole position used in the present study following Paper II. The grain
velocities cannot therefore be constrained better than
in
the pole position used in the present study following Paper II. The grain
velocities cannot therefore be constrained better than 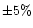 .
For a more rigorous check on the derived pole positions and the grain velocities,
intensity scans across the observed image along the directions
.
For a more rigorous check on the derived pole positions and the grain velocities,
intensity scans across the observed image along the directions
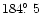 (b),
(b),
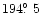 (c),
(c),
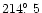 (d),
(d),
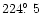 (e, the sunward direction),
(e, the sunward direction),
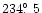 (f),
(f),
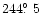 (g) and
(g) and
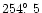 (h),
divided by the scans along the
same directions across the simulated coma of composition in Table 3
are compared with the simulated scans in Fig. 8 (lower panel).
(h),
divided by the scans along the
same directions across the simulated coma of composition in Table 3
are compared with the simulated scans in Fig. 8 (lower panel).
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{ms8445f8.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg265.gif) |
Figure 8:
Top: the processed observed image as in Fig. 5 showing the directions of scans.
Lower panel:
intensity scans across the observed (dashed line) and simulated
(solid line) images along directions
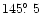 a),
a),
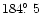 b),
b),
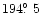 c),
c),
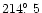 d),
d),
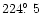 e), e),
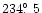 f),
f),
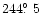 g),
g),
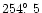 h) and
h) and
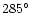 i), divided by the scans along the
same directions across the simulated coma of composition in Table 3.
i), divided by the scans along the
same directions across the simulated coma of composition in Table 3. |
The directions are marked on the observed image in the top panel.
The nucleus rotated by
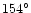 during the interval of time between the
ejections of the two extreme sections of the shells.
The cuts along the directions
during the interval of time between the
ejections of the two extreme sections of the shells.
The cuts along the directions
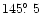 (a) and
(a) and
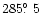 (i) are across the equatorial shells. The location and width
of the shells
match reasonably well over a range of hour angle of the Sun spanning
(i) are across the equatorial shells. The location and width
of the shells
match reasonably well over a range of hour angle of the Sun spanning
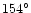 for the high latitude shells as well as the two cuts
across the equatorial shells.
The cuts along the directions 'b', 'c' and 'h' are contaminated by
the equatorial shells.
For all the cuts, at distances larger than
for the high latitude shells as well as the two cuts
across the equatorial shells.
The cuts along the directions 'b', 'c' and 'h' are contaminated by
the equatorial shells.
For all the cuts, at distances larger than
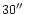 -
-
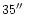 ,
deviations
between the observed and simulated cuts become noticeable. This may be
attributed to low intensity level of the observed image at these distances
as a result of which the errors associated with improper sky subtraction increase rapidly,
as indicated by the large error bars in Figs. 5 and 7.
The simulated image also suffers from limitations due to under-sampling
of the shells of only 8 rotations and coma of 13 rotations.
The deviations may also be due to the simplicity of the model which
does not take into
account the grain evolution processes like evaporation or splitting. These
processes alter
,
deviations
between the observed and simulated cuts become noticeable. This may be
attributed to low intensity level of the observed image at these distances
as a result of which the errors associated with improper sky subtraction increase rapidly,
as indicated by the large error bars in Figs. 5 and 7.
The simulated image also suffers from limitations due to under-sampling
of the shells of only 8 rotations and coma of 13 rotations.
The deviations may also be due to the simplicity of the model which
does not take into
account the grain evolution processes like evaporation or splitting. These
processes alter  of the grains and hence their dynamics.
There is also a gradual increase in the intensity of the first shell
from morning till evening (a-i). This may be due to the assumption
of uniform dust emission from dawn till dusk made in the simulation of
the coma, which is used to normalize the intensity. The simulated "shell+coma''
profile may be unaffected because of similar assumptions for simulating
the shells. The local E-W asymmetry appears to smoothen out in the outer
regions.
In any case, inferring the grain composition by matching the observed separation and width
of the first few shells alone
will be questionable because a variety of factors such as
grain size distribution, spread in porosity and organic content of the grains
determine the average value and spread in
of the grains and hence their dynamics.
There is also a gradual increase in the intensity of the first shell
from morning till evening (a-i). This may be due to the assumption
of uniform dust emission from dawn till dusk made in the simulation of
the coma, which is used to normalize the intensity. The simulated "shell+coma''
profile may be unaffected because of similar assumptions for simulating
the shells. The local E-W asymmetry appears to smoothen out in the outer
regions.
In any case, inferring the grain composition by matching the observed separation and width
of the first few shells alone
will be questionable because a variety of factors such as
grain size distribution, spread in porosity and organic content of the grains
determine the average value and spread in
 of the ensemble. Fortunately, these factors influence
the colour and the phase dependence of
polarization at different wavelengths in different ways (Figs. 3 and 4).
Hence as attempted in the present investigation, the
spatial match must be accompanied by comparisons of (1)
colour and (2) polarization of the observed and
simulated shells (Figs. 3 and 5). The derived range in porosity and organic
fraction must
explain the published phase curves in three colours (Fig. 6). This places
further constraints on the derived values of p and
of the ensemble. Fortunately, these factors influence
the colour and the phase dependence of
polarization at different wavelengths in different ways (Figs. 3 and 4).
Hence as attempted in the present investigation, the
spatial match must be accompanied by comparisons of (1)
colour and (2) polarization of the observed and
simulated shells (Figs. 3 and 5). The derived range in porosity and organic
fraction must
explain the published phase curves in three colours (Fig. 6). This places
further constraints on the derived values of p and 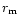 .
However, there are limitations
in the present model which should not be overlooked. As explained in
the following sections, Mie theory does not accurately
predict the polarization vs. phase curves of porous grains
which are not homogeneous. Lack of our understanding
of the nature of the organic component limits the reliability of the
derived compositions. If the composition of
the organic material assumed in Sect. 4.2 is changed by including
the extremely reddish material inferred by Tegler and Romanishin (2000)
in the Kuiper-belt objects, the fitted fraction of Aol will be modified.
This may also change the best fitting size distribution as this parameter
was constrained to explain the colour of the grains. Further,
despite the availability of an extensive and wide range of
data set on this comet, the inclusion of a large parameter space will
hinder in getting a unique solution due to cross talk between the effects
of different parameters.
.
However, there are limitations
in the present model which should not be overlooked. As explained in
the following sections, Mie theory does not accurately
predict the polarization vs. phase curves of porous grains
which are not homogeneous. Lack of our understanding
of the nature of the organic component limits the reliability of the
derived compositions. If the composition of
the organic material assumed in Sect. 4.2 is changed by including
the extremely reddish material inferred by Tegler and Romanishin (2000)
in the Kuiper-belt objects, the fitted fraction of Aol will be modified.
This may also change the best fitting size distribution as this parameter
was constrained to explain the colour of the grains. Further,
despite the availability of an extensive and wide range of
data set on this comet, the inclusion of a large parameter space will
hinder in getting a unique solution due to cross talk between the effects
of different parameters.
For reasons explained in Sect. 4.2,
the present technique cannot be used to identify the mineralogy of the
silicates in the grains although distinction can be made between the low and high Mg content
silicates based on the photometric and polarization colours (Figs. 3 and 4). Such investigations
are best made using IR spectroscopy
(Hayward et al. 2000; Wooden et al. 1999).
However, the derived porosities and organic contents
in the present work can help in constraining the IR continuum, and hence the
two techniques are complementary to one another.


Up: A photometric-dynamic model to
Copyright ESO 2002
![]() region by Hayward et al. (2000) and
Wooden et al. (1999). In the visible and near IR regions,
it is futile to identify the Mg rich
silicates either in glassy or crystalline form in the composite
grains using their
scattered radiation, as presence of
even a small amount of organic content of 1/12 by weight
will be sufficient to significantly
alter the refractive index of the composite grain.
Hence silicates were sub grouped
into three classes depending on the absorption index k:
region by Hayward et al. (2000) and
Wooden et al. (1999). In the visible and near IR regions,
it is futile to identify the Mg rich
silicates either in glassy or crystalline form in the composite
grains using their
scattered radiation, as presence of
even a small amount of organic content of 1/12 by weight
will be sufficient to significantly
alter the refractive index of the composite grain.
Hence silicates were sub grouped
into three classes depending on the absorption index k:
![]() m, 0.4845
m, 0.4845 ![]() m and
0.3650
m and
0.3650 ![]() m corresponding to aperture polarimetry observations by
Ganesh et al. (1998) and Manset & Bastien (1998) were
computed.
For a proper match with these observations over the entire range of
phase angles, combinations of grain types and
proper choice of their size distribution are essential.
Hanner size distribution (Hanner 1985)
m corresponding to aperture polarimetry observations by
Ganesh et al. (1998) and Manset & Bastien (1998) were
computed.
For a proper match with these observations over the entire range of
phase angles, combinations of grain types and
proper choice of their size distribution are essential.
Hanner size distribution (Hanner 1985)
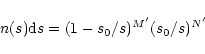
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f2.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg174.gif)
![]() .
In the present work it is attempted to investigate
the relative fraction
of the grain type and their size distributions
separately in the coma and the shells.
.
In the present work it is attempted to investigate
the relative fraction
of the grain type and their size distributions
separately in the coma and the shells.
![]() and
and
![]() for the grain types in Table 2.
The pole positions and latitude of the
sources are adapted from Paper II.
The grain velocities computed using Eq. (2)
with
v0 = 0.63 kms-1 were found to be within
for the grain types in Table 2.
The pole positions and latitude of the
sources are adapted from Paper II.
The grain velocities computed using Eq. (2)
with
v0 = 0.63 kms-1 were found to be within
![]() -
-![]() to the values computed using Eq. (1). The latter was used
in the simulations.
The coma was simulated by considering emission from a grid on the
comet at intervals of
to the values computed using Eq. (1). The latter was used
in the simulations.
The coma was simulated by considering emission from a grid on the
comet at intervals of ![]() in latitude and
in latitude and
![]() in longitude,
where
in longitude,
where ![]() is the latitude of the point on the grid.
The sources are assumed to be active when sunlit.
The trajectories
of the dust grains are computed assuming collimated emissions. In
reality, the emission may be spread over a cone. Further, the velocity
of the grains will have a spread due to deviation from their assumed
sphericity, finite size of the active
regions and possible irregular local terrain. Their cumulative effect
will produce a broadening of the shells. As it is difficult to model each
of these effects, the sky plane position of the grains
were convolved
with a Gaussian-random profile with a sigma of 1
is the latitude of the point on the grid.
The sources are assumed to be active when sunlit.
The trajectories
of the dust grains are computed assuming collimated emissions. In
reality, the emission may be spread over a cone. Further, the velocity
of the grains will have a spread due to deviation from their assumed
sphericity, finite size of the active
regions and possible irregular local terrain. Their cumulative effect
will produce a broadening of the shells. As it is difficult to model each
of these effects, the sky plane position of the grains
were convolved
with a Gaussian-random profile with a sigma of 1
![]() 5.
To include the effect of spreading with time,
the sigma was allowed to increase by 0
5.
To include the effect of spreading with time,
the sigma was allowed to increase by 0
![]() 25 per day.
Due to rotation of the nucleus, grains in the expanding jets are swept
along the azimuth of the comet giving the appearance of a set of shells,
one shell per rotation.
The simulated images contain 8 shells and coma
dust ejected between 0 - 150 hr.
25 per day.
Due to rotation of the nucleus, grains in the expanding jets are swept
along the azimuth of the comet giving the appearance of a set of shells,
one shell per rotation.
The simulated images contain 8 shells and coma
dust ejected between 0 - 150 hr.
![]() ),
),
![]() for distribution 'c',
for distribution 'c',
![]() for 'a' and
for 'a' and
![]() for 'b'. The anti-correlation in colour and polarization
as pointed out by Kolokolova et al. (2001)
is clearly noticeable for 'a' and 'b': the collection
'b' (right) which has larger grains has lower polarization but larger colour
than the distribution 'a' (middle). Contrary to scattering behavior of
sub-micron sized grains,
the absorptive grains in population 'c' are redder compared to that in 'a'which contains additional larger grains. The reddening is found to increase
with the refractive index of the grain either due to increase of organic
fraction or reduction in porosity. It is marginally higher for Aol
compared to the less absorptive SiA. As pointed out by
Kolokolova et al. (2001), a grain may be redder if its
size parameter x is just beyond the scattering peak. The scattering peak
occurs at
for 'b'. The anti-correlation in colour and polarization
as pointed out by Kolokolova et al. (2001)
is clearly noticeable for 'a' and 'b': the collection
'b' (right) which has larger grains has lower polarization but larger colour
than the distribution 'a' (middle). Contrary to scattering behavior of
sub-micron sized grains,
the absorptive grains in population 'c' are redder compared to that in 'a'which contains additional larger grains. The reddening is found to increase
with the refractive index of the grain either due to increase of organic
fraction or reduction in porosity. It is marginally higher for Aol
compared to the less absorptive SiA. As pointed out by
Kolokolova et al. (2001), a grain may be redder if its
size parameter x is just beyond the scattering peak. The scattering peak
occurs at
![]() for absorptive grains with
an effective refractive index of
for absorptive grains with
an effective refractive index of ![]()
![]() corresponding to
corresponding to
![]() and
and
![]() .
For less absorptive grains of pure silicates
of effective refractive index
.
For less absorptive grains of pure silicates
of effective refractive index ![]()
![]() corresponding to
corresponding to
![]() porosity,
the peak occurs
at
porosity,
the peak occurs
at
![]() (Wickramasinghe 1973).
For the average grain size of
(Wickramasinghe 1973).
For the average grain size of
![]() at the broad peak in Fig. 2
for distribution 'c', the size parameters at
at the broad peak in Fig. 2
for distribution 'c', the size parameters at
![]() and
and
![]() are 2.2 and 4.4 respectively. This range in size parameter is beyond the
scattering peak for absorptive grains and before for the pure silicates.
This explains the red colour of the absorptive grains and the blue colour
of the less absorptive ones.
Further, for this distribution
are 2.2 and 4.4 respectively. This range in size parameter is beyond the
scattering peak for absorptive grains and before for the pure silicates.
This explains the red colour of the absorptive grains and the blue colour
of the less absorptive ones.
Further, for this distribution
![]() ,
the reason for this large polarization colour is that
in this domain of
,
the reason for this large polarization colour is that
in this domain of
![]() ,
the grain becomes increasingly forward
scattering with
increase in its size parameter.
Blue light is therefore more forward scattered than the red. With increase in the transmitted
part of blue light
which is parallelly polarized (negative polarization) the resultant
polarization is lower compared to that in red.
On the other hand, for the large grain population 'b',
,
the grain becomes increasingly forward
scattering with
increase in its size parameter.
Blue light is therefore more forward scattered than the red. With increase in the transmitted
part of blue light
which is parallelly polarized (negative polarization) the resultant
polarization is lower compared to that in red.
On the other hand, for the large grain population 'b',
![]() ,
which is opposite to the observed trend for comets. Therefore, the difference
in the grain populations in the coma and shells may in most part be due to difference
in the silicate to organic ratio rather than difference in grain sizes.
,
which is opposite to the observed trend for comets. Therefore, the difference
in the grain populations in the coma and shells may in most part be due to difference
in the silicate to organic ratio rather than difference in grain sizes.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{ms8445f4.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg207.gif)
![\begin{figure}
\par\includegraphics[width=14.5cm,clip]{ms8445f7.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg246.gif)
![]() ). The polarization
contrast between the coma and the shells are therefore reduced in these plots.
The maximum and minimum value of polarization in the map however correspond to
). The polarization
contrast between the coma and the shells are therefore reduced in these plots.
The maximum and minimum value of polarization in the map however correspond to
![]() in the bright regions and
in the bright regions and ![]() beyond the 4th shell in the sunward
direction.
beyond the 4th shell in the sunward
direction.
![]() and the acceleration
and the acceleration ![]() of the grains.
The later two quantities depend on the size distribution and the nature
of the grains.
For the geometry on 10 April, 1997, the uncertainty
in the computed separation of the shells from the source at
of the grains.
The later two quantities depend on the size distribution and the nature
of the grains.
For the geometry on 10 April, 1997, the uncertainty
in the computed separation of the shells from the source at ![]() ,
is found to be
,
is found to be
![]() along the projected sunward direction for a change in
along the projected sunward direction for a change in
![]() by
by
![]() and
and
![]() by
by
![]() .
The model thus reproduces the shells
within an accuracy of
.
The model thus reproduces the shells
within an accuracy of ![]() in the shell separation corresponding
to the uncertainty of
in the shell separation corresponding
to the uncertainty of
![]() in
the pole position used in the present study following Paper II. The grain
velocities cannot therefore be constrained better than
in
the pole position used in the present study following Paper II. The grain
velocities cannot therefore be constrained better than ![]() .
For a more rigorous check on the derived pole positions and the grain velocities,
intensity scans across the observed image along the directions
.
For a more rigorous check on the derived pole positions and the grain velocities,
intensity scans across the observed image along the directions
![]() (b),
(b),
![]() (c),
(c),
![]() (d),
(d),
![]() (e, the sunward direction),
(e, the sunward direction),
![]() (f),
(f),
![]() (g) and
(g) and
![]() (h),
divided by the scans along the
same directions across the simulated coma of composition in Table 3
are compared with the simulated scans in Fig. 8 (lower panel).
(h),
divided by the scans along the
same directions across the simulated coma of composition in Table 3
are compared with the simulated scans in Fig. 8 (lower panel).
![\begin{figure}
\par\includegraphics[width=5.4cm,clip]{ms8445f8.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg265.gif)