The intensity of light
![]() and polarization
and polarization
![]() scattered by the grain towards
the observer are given by (Krishnaswamy & Shah 1987):
scattered by the grain towards
the observer are given by (Krishnaswamy & Shah 1987):
| = | 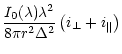 |
(18) | |
| = | (19) |
The position of the grain in the shell projected on the sky plane at a given
time was thus calculated using Eqs. (13) and (14) and the intensity and
polarization of light
scattered by it was computed using the Eqs. (18) and (19).
The colour is calculated following the definition by Jewitt & Meech
(1986) as the normalized reflectivity gradient expressed in ![]() ,
,
![]() between
wavelengths
between
wavelengths ![]() and
and ![]() ,
where dS/d
,
where dS/d![]() is the rate
of change of reflectivity with wavelength and
is the rate
of change of reflectivity with wavelength and
![]() is the mean
reflectivity.
is the mean
reflectivity.
Copyright ESO 2002