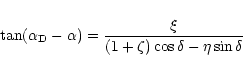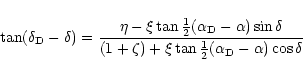Up: A photometric-dynamic model to
Subsections
The computer simulations are based on the basic concepts introduced
by Sekanina (1981, 1991)
and Sekanina & Larson (1984). Except for the outburst
events during 1995, which were sporadic activities, the dust grains are assumed
to be ejected continuously from the sources
radially outwards, from local sunrise to sunset.
The ejected grains are subjected
to the gravitational attraction of the Sun and the Solar radiation pressure
force in the opposite direction. In the present work, since we study the
shells which are close to the nucleus within a distance of 
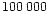 km, it is assumed that
dust grains follow the same Keplerian motion as that of the comet due to solar
gravity. Thus, relative to the
comet, the position of the dust grain can be calculated from its
initial velocity,
the radiation pressure force and the ejection geometry.
km, it is assumed that
dust grains follow the same Keplerian motion as that of the comet due to solar
gravity. Thus, relative to the
comet, the position of the dust grain can be calculated from its
initial velocity,
the radiation pressure force and the ejection geometry.
The velocity
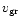 attained by the grains
due to gas drag (Probstein 1969) can be calculated
using the relation by Sekanina (1981):
attained by the grains
due to gas drag (Probstein 1969) can be calculated
using the relation by Sekanina (1981):
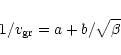 |
(1) |
and also the following equation by Fulle (1987)
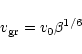 |
(2) |
where  is the ratio of the force due to solar radiation
pressure on the grain to the gravitational force.
Sekanina & Larson (1984) have used Eq. (1) successfully for emission from
discrete sources, and pointed out that it is valid for slightly absorbing
grains with
is the ratio of the force due to solar radiation
pressure on the grain to the gravitational force.
Sekanina & Larson (1984) have used Eq. (1) successfully for emission from
discrete sources, and pointed out that it is valid for slightly absorbing
grains with
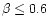 .
The acceleration
.
The acceleration 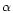 due to solar
radiation pressure depends on the nature of the grain and the heliocentric
distance. Using the definition of
due to solar
radiation pressure depends on the nature of the grain and the heliocentric
distance. Using the definition of  ,
,
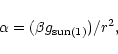 |
(3) |
where
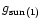 is the acceleration due to solar gravity at one
AU (
is the acceleration due to solar gravity at one
AU (
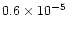 kms-2) and
r the heliocentric distance of the comet.
The value of
kms-2) and
r the heliocentric distance of the comet.
The value of  can be calculated
for a grain of given size and composition
using the relation by Finson & Probstein (1968):
can be calculated
for a grain of given size and composition
using the relation by Finson & Probstein (1968):
where
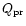 is the scattering efficiency for radiation pressure
of the grain, s its radius and
is the scattering efficiency for radiation pressure
of the grain, s its radius and 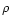 its density.
its density.
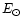 is the total solar radiation per second, c the velocity
of light,
is the total solar radiation per second, c the velocity
of light, 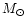 the mass of the Sun and G the universal gravitational
constant.
In the present investigation, the grain size is allowed to vary from
the mass of the Sun and G the universal gravitational
constant.
In the present investigation, the grain size is allowed to vary from
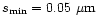 to
to
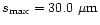 with Hanner (1985)
size distribution law.
Since
the radiation pressure parameter
with Hanner (1985)
size distribution law.
Since
the radiation pressure parameter
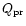 of a
grain material depends both on its size and
the wavelength of radiation,
the value of
of a
grain material depends both on its size and
the wavelength of radiation,
the value of  for a grain of radius s was calculated using the more
precise relation
for a grain of radius s was calculated using the more
precise relation
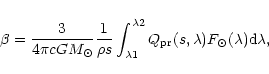 |
(6) |
where,
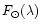 is the mean total solar radiation from the sun per second
per Angstrom at the wavelength
is the mean total solar radiation from the sun per second
per Angstrom at the wavelength 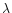 .
The above integration was carried out from
.
The above integration was carried out from
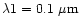 to
to
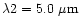 .
.
In the simulation, the path of the dust grain
ejected radially from an active region at a comet-o-centric longitude u, latitude 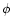 and the nuclear radius R is calculated as a function of time.
Figure 1 shows the ideal case of a spherically symmetric nucleus centered at C.
and the nuclear radius R is calculated as a function of time.
Figure 1 shows the ideal case of a spherically symmetric nucleus centered at C.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{ms8445f1.eps}\end{figure}](/articles/aa/full/2002/04/aa8445/Timg74.gif) |
Figure 1:
A model to compute the sky plane coordinates of the ejected dust grains.
The comet centered at C is assumed to be spherically symmetric. The grain from the
source at G is ejected with velocity
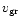 .
The north pole of the comet is
at .
The north pole of the comet is
at 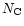 ,
CPE is the direction of Earth's celestial pole, E and S are the
sub-Earth and sub-Sun points respectively. See text for more details. ,
CPE is the direction of Earth's celestial pole, E and S are the
sub-Earth and sub-Sun points respectively. See text for more details. |
The sub-Sun and sub-Earth points are S and E respectively and 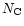 is the North pole of the comet.
The direction of the Earth's north pole is along
is the North pole of the comet.
The direction of the Earth's north pole is along
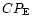 .
The ascending node of the comet's equator on the Earth's equator
is
.
The ascending node of the comet's equator on the Earth's equator
is
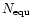 and that on the ecliptic is indicated by
and that on the ecliptic is indicated by
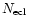 .
Components of
.
Components of 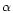 parallel to the plane of the comet's equator and
perpendicular to it
are
parallel to the plane of the comet's equator and
perpendicular to it
are
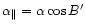 parallel to SF and
parallel to SF and
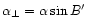 parallel to ST respectively where
parallel to ST respectively where
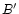 is the comet-o-centric latitude of the Sun.
The longitude of the source and the dust grains are measured from
is the comet-o-centric latitude of the Sun.
The longitude of the source and the dust grains are measured from
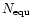 along the direction of rotation of the comet. The longitude of the sub-Earth
point E is
along the direction of rotation of the comet. The longitude of the sub-Earth
point E is 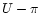 and the angle
and the angle
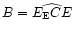 is its latitude.
Dust grains are ejected radially outwards with the velocity
is its latitude.
Dust grains are ejected radially outwards with the velocity
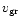 from an
active source
from an
active source
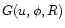 ,
where
,
where
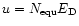 and
and
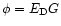 .
Strictly speaking, the grain attains this velocity
after it is dragged by the subliming gas to a few nuclear radii.
However, considering the vast spatial extent of the shell and jet structures
of several rotations which are being modeled, this distance can be ignored.
Relative to the comet, during time t, the dust traverses a
distance
.
Strictly speaking, the grain attains this velocity
after it is dragged by the subliming gas to a few nuclear radii.
However, considering the vast spatial extent of the shell and jet structures
of several rotations which are being modeled, this distance can be ignored.
Relative to the comet, during time t, the dust traverses a
distance
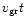 in the radial direction and
a distance
in the radial direction and
a distance
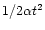 along the Sun - comet direction due to
solar radiation pressure.
along the Sun - comet direction due to
solar radiation pressure.
The position (
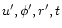 )
of the grain at time t reckoned after ejection is given by:
)
of the grain at time t reckoned after ejection is given by:
where
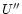 ,
the longitude of the sub-Sun point is given by
,
the longitude of the sub-Sun point is given by
The expressions in Eq. (7) are valid provided the direction and magnitude
of 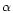 is constant. For the observations during February-May 1997, since we model only up
to a maximum of 8 shells,
a constant value for
is constant. For the observations during February-May 1997, since we model only up
to a maximum of 8 shells,
a constant value for 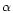 during the period of 8 rotations
may be a valid assumption for comet Hale-Bopp with a period of
11.34 hr (Jorda et al. 1997; Licandro et al. 1998). For
the 1995-96 images, slow apparent
motion of the comet again justifies such an assumption.
during the period of 8 rotations
may be a valid assumption for comet Hale-Bopp with a period of
11.34 hr (Jorda et al. 1997; Licandro et al. 1998). For
the 1995-96 images, slow apparent
motion of the comet again justifies such an assumption.
The angles
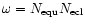 ,
,
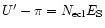 can be calculated from the following relations:
can be calculated from the following relations:
where i is the inclination of the comet's equator to the ecliptic.
The angles
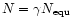 and J, the inclination of the comet's equator to the Earth's
equator are related to the right ascension and declination of the comet's pole:
and J, the inclination of the comet's equator to the Earth's
equator are related to the right ascension and declination of the comet's pole:
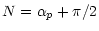 |
|
|
|
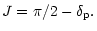 |
|
|
(9) |
The angles U,
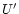 ,
B,
,
B,
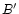 and the position angle Pof the north pole of the comet projected on the sky plane were
calculated using the equations used for calculating the planet-o-centric
positions of the satellite with respect to the planets
(Rhode & Sinclair 1992):
and the position angle Pof the north pole of the comet projected on the sky plane were
calculated using the equations used for calculating the planet-o-centric
positions of the satellite with respect to the planets
(Rhode & Sinclair 1992):
where 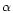 ,
,
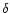 ,
l and b are the geocentric right ascension,
declination, heliocentric ecliptic longitude and latitude of the comet
respectively. The angle
,
l and b are the geocentric right ascension,
declination, heliocentric ecliptic longitude and latitude of the comet
respectively. The angle
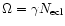 can be calculated using the following relations:
can be calculated using the following relations:
The angles U, P and B are not directly needed for calculating the trajectory of
the dust grain. These are nevertheless useful to visualize the defect of
solar illumination on the comet, the orientation and
aspect angle of the dust jet and shell patterns.
The comet-o-centric coordinates
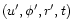 referred to the comet's equator were
calculated using Eq. (7).
These were transformed to the comet-o-centric Earth's equatorial coordinates
referred to the comet's equator were
calculated using Eq. (7).
These were transformed to the comet-o-centric Earth's equatorial coordinates
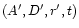 of the grain using the following
equations:
of the grain using the following
equations:
The comet-o-centric equatorial coordinate of the source at
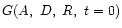 is shown in Fig. 1.
is shown in Fig. 1.
The projected location of the grain on the sky plane with respect to the
comet center is obtained by computing its differential Earth's equatorial
co-ordinates using the following equations (Gurnette & Woolley 1960):
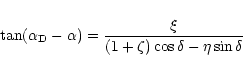 |
(13) |
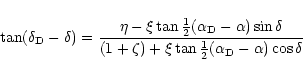 |
(14) |
where
where
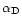 and
and
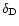 are the geocentric right ascension and declination
of the grain and
are the geocentric right ascension and declination
of the grain and 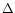 its geocentric distance.
These rigorous expressions in Eqs. (13)-(17) are actually used for
calculating the differential coordinates of satellites with respect to the
primary without any assumptions regarding their latitudes. These are therefore
applicable in the present case of the comet-dust geometry.
its geocentric distance.
These rigorous expressions in Eqs. (13)-(17) are actually used for
calculating the differential coordinates of satellites with respect to the
primary without any assumptions regarding their latitudes. These are therefore
applicable in the present case of the comet-dust geometry.


Up: A photometric-dynamic model to
Copyright ESO 2002
![]()
![]() km, it is assumed that
dust grains follow the same Keplerian motion as that of the comet due to solar
gravity. Thus, relative to the
comet, the position of the dust grain can be calculated from its
initial velocity,
the radiation pressure force and the ejection geometry.
km, it is assumed that
dust grains follow the same Keplerian motion as that of the comet due to solar
gravity. Thus, relative to the
comet, the position of the dust grain can be calculated from its
initial velocity,
the radiation pressure force and the ejection geometry.
![]() attained by the grains
due to gas drag (Probstein 1969) can be calculated
using the relation by Sekanina (1981):
attained by the grains
due to gas drag (Probstein 1969) can be calculated
using the relation by Sekanina (1981):
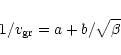
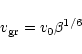
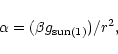
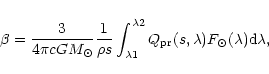
![]() and the nuclear radius R is calculated as a function of time.
Figure 1 shows the ideal case of a spherically symmetric nucleus centered at C.
and the nuclear radius R is calculated as a function of time.
Figure 1 shows the ideal case of a spherically symmetric nucleus centered at C.
![]() )
of the grain at time t reckoned after ejection is given by:
)
of the grain at time t reckoned after ejection is given by:
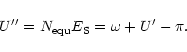
![]() ,
,
![]() can be calculated from the following relations:
can be calculated from the following relations:
![]() referred to the comet's equator were
calculated using Eq. (7).
These were transformed to the comet-o-centric Earth's equatorial coordinates
referred to the comet's equator were
calculated using Eq. (7).
These were transformed to the comet-o-centric Earth's equatorial coordinates
![]() of the grain using the following
equations:
of the grain using the following
equations: