

Up: Gravitational instability of finite
Subsections
3 Isothermal gaseous spheres in general relativity
3.1 The equations governing equilibrium
We now address the structure and the stability of isothermal gas spheres in the context of general relativity. The Einstein field equations of general relativity are expressed as
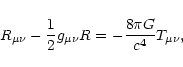 |
(97) |
where
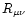 is the Ricci tensor,
is the Ricci tensor,
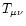 the energy-momentum tensor and
the energy-momentum tensor and
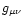 the metric tensor defined by
the metric tensor defined by
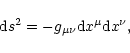 |
(98) |
where ds is the invariant interval between two neighbouring space-time events.
In the following, we shall restrict ourselves to spherically symmetric systems with motions, if any, only in the radial directions. Under these assumptions, the metric can be written in the form
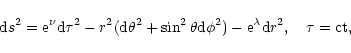 |
(99) |
where 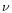 and
and 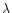 are functions of r and
are functions of r and 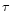 only. The energy-momentum tensor is assumed to be that for a perfect fluid
only. The energy-momentum tensor is assumed to be that for a perfect fluid
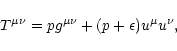 |
(100) |
where
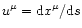 is the fluid four-velocity, p is the isotropic
pressure and
is the fluid four-velocity, p is the isotropic
pressure and 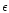 is the energy density including the rest mass.
is the energy density including the rest mass.
The equations of general relativity governing the hydrostatic equilibrium of a spherical distribution of matter are well known. They are given by (see, e.g., Weinberg 1972)
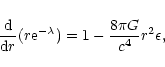 |
(101) |
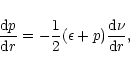 |
(102) |
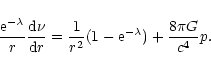 |
(103) |
These equations can be deduced from the Einstein Eq. (97). However, Eq. (102) can be obtained more directly from the local law of energy-momentum conservation,
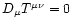 ,
which is also contained in the Einstein equations.
,
which is also contained in the Einstein equations.
Equations (101)-(103) can be combined to give
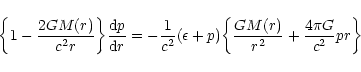 |
(104) |
and
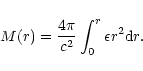 |
(105) |
These equations are known as the Oppenheimer-Volkoff equations. They extend the classical condition of hydrostatic equilibrium for a star to the context of general relativity. Using Eqs. (101) and (103), we find that the metric functions
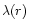 and
and 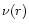 satisfy the relations
satisfy the relations
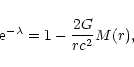 |
(106) |
and
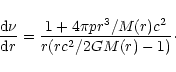 |
(107) |
In the empty space outside the star,
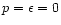 .
Therefore, if M=M(R) denotes the total mass-energy of the star, Eqs. (106), (107) become for r>R
.
Therefore, if M=M(R) denotes the total mass-energy of the star, Eqs. (106), (107) become for r>R
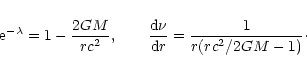 |
(108) |
The second equation is readily integrated in
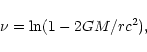 |
(109) |
where we have taken the constant of integration to be zero by convention.
Substituting the foregoing expressions for 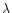 and
and 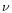 in Eq. (99), we obtain the well-known Schwarzschild's form of the metric outside a star
in Eq. (99), we obtain the well-known Schwarzschild's form of the metric outside a star
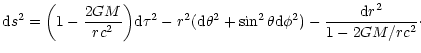 |
|
|
(110) |
This metric is singular at
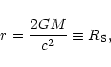 |
(111) |
where 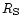 is the Schwazschild radius appropriate to the mass M. This does not mean that spacetime is singular at that radius but only that this particular metric is. Indeed, the singularity can be removed by a judicious change of coordinate system (see, e.g., Weinberg 1972). When
is the Schwazschild radius appropriate to the mass M. This does not mean that spacetime is singular at that radius but only that this particular metric is. Indeed, the singularity can be removed by a judicious change of coordinate system (see, e.g., Weinberg 1972). When
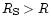 ,
the star is a black hole and no particle or even light can leave the region
,
the star is a black hole and no particle or even light can leave the region
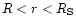 .
However, in our case the discussion does not arise because
.
However, in our case the discussion does not arise because
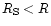 .
Indeed, for a gaseous sphere in hydrostatic equilibrium, it can be shown that the radius of the configuration is necessarily restricted by the inequality (Buchdahl 1959)
.
Indeed, for a gaseous sphere in hydrostatic equilibrium, it can be shown that the radius of the configuration is necessarily restricted by the inequality (Buchdahl 1959)
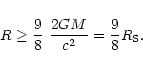 |
(112) |
Therefore, the points exterior to the star always satisfy
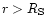 .
.
3.2 The equation of state
To close the system of Eqs. (104), (105), we need to
specify an equation of state relating the pressure p to the energy
density 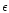 .
Quite generally, the first law of thermodynamics
can be expressed as
.
Quite generally, the first law of thermodynamics
can be expressed as
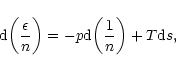 |
(113) |
or, equivalently,
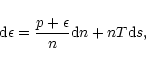 |
(114) |
where n is the baryon number density and s the entropy per baryon in rest frame. It must be completed by two equations of state p=p(n,s) and T=T(n,s). Then, Eq. (114) can be integrated to give
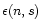 (see, e.g., Misner et al. 1973).
(see, e.g., Misner et al. 1973).
We shall assume in the following that the term Tds in Eq. (114) can be neglected. This simplification arises in two different situations. In the case of neutron stars or white dwarfs, the thermal energy kT is much smaller than the Fermi energy, so the neutrons or the electrons are completely degenerate (
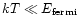 ). On the other hand, in supermassive stars, temperature and entropy are important but convection keeps the star stired up and produces a uniform entropy distribution (
). On the other hand, in supermassive stars, temperature and entropy are important but convection keeps the star stired up and produces a uniform entropy distribution (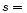 const.). In these two important situations, the first law of thermodynamics reduces to
const.). In these two important situations, the first law of thermodynamics reduces to
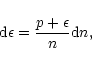 |
(115) |
and we just require one equation of state p=p(n). We shall consider an equation of state of the form
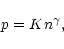 |
(116) |
where K and 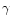 are constant. It is easy to check that the general solution of Eq. (115) with Eq. (116) is
are constant. It is easy to check that the general solution of Eq. (115) with Eq. (116) is
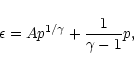 |
(117) |
where A is a constant. Systems obeying the pressure-energy density relation (117) with 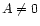 have been considered by Tooper (1965). Since the relation between
have been considered by Tooper (1965). Since the relation between 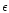 and p is essentially a power-law, these systems generalize the polytropes of Newtonian theory. We shall here consider the limiting situation A=0. In that case, Eq. (117) reduces to the so-called "gamma law'' equation of state
and p is essentially a power-law, these systems generalize the polytropes of Newtonian theory. We shall here consider the limiting situation A=0. In that case, Eq. (117) reduces to the so-called "gamma law'' equation of state
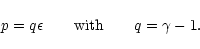 |
(118) |
Since the relation between p and 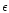 is linear, this equation of state extends the theory of isothermal spheres to the context of general relativity. As noted by Chandrasekhar (1972), for this equation of state, the Oppenheimer-Volkoff equations become mathematically similar to those describing a classical isothermal gas (the so-called Emden equations).
is linear, this equation of state extends the theory of isothermal spheres to the context of general relativity. As noted by Chandrasekhar (1972), for this equation of state, the Oppenheimer-Volkoff equations become mathematically similar to those describing a classical isothermal gas (the so-called Emden equations).
An equation of state of the form (118) has been introduced in different situations:
(i) This equation of state prevails in the highly energetic core of neutron stars where the matter is ultra-relativistic and completely degenerate (Oppenheimer & Volkoff 1939; Misner & Zapolsky 1964; Meltzer & Thorne 1966). If the system is modelled as a pure collection of noninteracting fermions, standard theory leads to (Chandraskhar 1942)
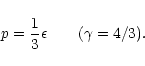 |
(119) |
In that case, the constant K which appears in Eq. (116) is explicitly given by
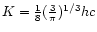 ,
where h is the Planck constant. Other versions of the equation of state have attempted to take into account nucleon-nucleon interactions or a spectrum of baryon species. Equations of the form (118) but with numerical coefficient other than 1/3 have sometimes been suggested. For example, Ambartsumyan & Saakyan (1961) have used an equation with q=1/13 (
,
where h is the Planck constant. Other versions of the equation of state have attempted to take into account nucleon-nucleon interactions or a spectrum of baryon species. Equations of the form (118) but with numerical coefficient other than 1/3 have sometimes been suggested. For example, Ambartsumyan & Saakyan (1961) have used an equation with q=1/13 (
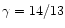 )
and Tsuruta & Cameron (1966) with q=1. The equation of state
)
and Tsuruta & Cameron (1966) with q=1. The equation of state
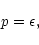 |
(120) |
was also introduced by Zel'dovich (1962) for a gas of baryons interacting through a vector meson field. This represents an extremely high pressure since the sound velocity,
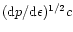 ,
is equal to the velocity of light for this value of q. This is clearly an upper bound. In the following, we shall consider a general equation of state of the form (118) with q in the range
,
is equal to the velocity of light for this value of q. This is clearly an upper bound. In the following, we shall consider a general equation of state of the form (118) with q in the range
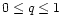 .
.
(ii) Bisnovatyi-Kogan & Zel'dovich (1969) and Bisnovatyi-Kogan & Thorne (1970) have considered the general relativistic equilibrium configuration of a gas whose temperature T is constant everywhere. In that case, the equation of state is given by (see Sect. 2)
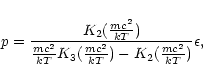 |
(121) |
which is again of the form (118). In particular,
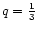 when
when
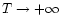 .
However, as Bisnovatyi-Kogan & Thorne emphasize, the equation of state (121) can only describe a "local'' thermodynamical equilibrium. Indeed, "global'' thermodynamical equilibrium in general relativity requires that the redshifted temperature e
.
However, as Bisnovatyi-Kogan & Thorne emphasize, the equation of state (121) can only describe a "local'' thermodynamical equilibrium. Indeed, "global'' thermodynamical equilibrium in general relativity requires that the redshifted temperature e
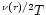 be uniform throughout the medium (Tolman 1934). Thus, the spheres described by Eq. (121) are not "isothermal'' in the general-relativistic sense; heat will slowly diffuse inward in them, upsetting the condition
be uniform throughout the medium (Tolman 1934). Thus, the spheres described by Eq. (121) are not "isothermal'' in the general-relativistic sense; heat will slowly diffuse inward in them, upsetting the condition 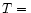 const. and trying to establish
const. and trying to establish
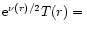 const. instead. However, since the hydrostatic Eqs. (104), (105) with the equation of state (118) are mathematically similar to the classical Emden equation for isothermal gas spheres, we shall call the equation of state (118) "isothermal'', following the terminology of Chandrasekhar (1972), although this is only correct in a local sense.
const. instead. However, since the hydrostatic Eqs. (104), (105) with the equation of state (118) are mathematically similar to the classical Emden equation for isothermal gas spheres, we shall call the equation of state (118) "isothermal'', following the terminology of Chandrasekhar (1972), although this is only correct in a local sense.
(iii) The equation of state (118) was also proposed by Saslaw et al. (1996) in a cosmological context to model the ultimate state of an Einstein-de Sitter universe that undergoes a phase transition caused by gravitational clustering. This phase transition can lead to the growth of a centrally concentrated distribution of matter so that the universe would pass from a statistically homogeneous state to a state of rotational symmetry around one point only. The resulting configuration neither expands nor contracts, so the global solution is stationary. According to Saslaw et al. (1996), this "isothermal universe'' would represent the ultimate astrophysical prediction.
(iv) Note finally that the equation of state
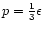 prevails in a medium where the pressure is entirely due to radiation (Chandrasekhar 1942).
prevails in a medium where the pressure is entirely due to radiation (Chandrasekhar 1942).
3.3 The general relativistic Emden equation
Considering the equation of state (118), we shall introduce the dimensionless variables 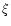 ,
,
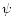 and
and 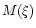 by the relations
by the relations
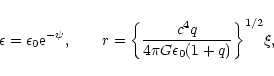 |
(122) |
and
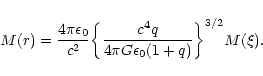 |
(123) |
In terms of the variables 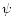 and
and 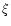 ,
Eqs. (104) and (105) can be reduced to the following dimensionless forms (Chandrasekhar 1972)
,
Eqs. (104) and (105) can be reduced to the following dimensionless forms (Chandrasekhar 1972)
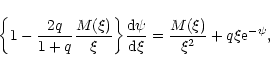 |
(124) |
and
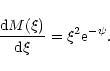 |
(125) |
In addition, the metric functions determined by Eqs. (106) and (102) can be expressed as
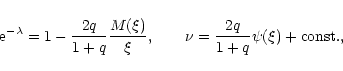 |
(126) |
where the constant is determined by the matching with the outer Schwarzschild solution (109) at r=R.
The Newtonian limit corresponds to
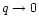 .
In that limit, Eqs. (124), (125) reduce to
.
In that limit, Eqs. (124), (125) reduce to
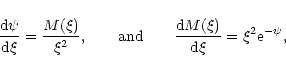 |
(127) |
and they combine to give Emden's equation
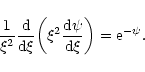 |
(128) |
Therefore, Eqs. (124), (125) represent the general relativistic equivalent of the Emden equation. Like in the Newtonian case, they admit a singular solution of the form (Chandrasekhar 1972)
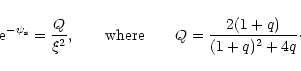 |
(129) |
The metric associated with the singular isothermal sphere is given explicitly by
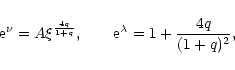 |
(130) |
where A is an unimportant constant. Considering now the regular solutions of Eqs. (124), (125), we can always suppose that
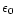 represents the energy density at the center of the configuration. Then, Eqs. (124), (125) must be solved with the boundary conditions
represents the energy density at the center of the configuration. Then, Eqs. (124), (125) must be solved with the boundary conditions
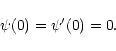 |
(131) |
The corresponding solution must be computed numerically. However, it is possible to determine its asymptotic behaviors explicitly. For
 ,
,
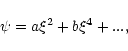 |
(132) |
with
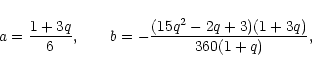 |
(133) |
and for
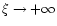 (Chandrasekhar 1972)
(Chandrasekhar 1972)
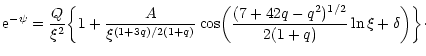 |
|
|
(134) |
The curve (134) intersects the singular solution (129) infinitely often at points that asymptotically increase geometrically in the ratio 1:
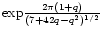 (see Fig. 8). Since the energy density
(see Fig. 8). Since the energy density 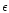 falls off as
falls off as 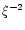 at large distances, the total mass-energy M is infinite. In practice, this "infinite mass problem'' does not arise because the isothermal equation of state (118) only holds in a finite region of space (e.g., the inner regions of a neutron star). For simplicity, we shall remedy this difficulty by assuming that our system is confined within a box of radius R, like in Sect. 2. This is clearly an idealization but it provides a well-posed model which captures the essential features of the system (see below) and which can be be studied in great detail without any further approximation.
at large distances, the total mass-energy M is infinite. In practice, this "infinite mass problem'' does not arise because the isothermal equation of state (118) only holds in a finite region of space (e.g., the inner regions of a neutron star). For simplicity, we shall remedy this difficulty by assuming that our system is confined within a box of radius R, like in Sect. 2. This is clearly an idealization but it provides a well-posed model which captures the essential features of the system (see below) and which can be be studied in great detail without any further approximation.
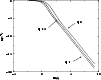 |
Figure 8:
Density profiles of the general relativistic Emden equation for different values of q. The profiles behaves like 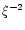 at large distances.
at large distances. |
If the system is enclosed within a box, the solution of Eqs. (124), (125) must be terminated at a radius  given by
given by
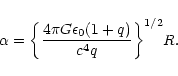 |
(135) |
It should be noted that  is a measure of the central energy density
is a measure of the central energy density
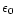 (for a given box radius R). Instead of
(for a given box radius R). Instead of  ,
we might prefer to consider the density contrast
,
we might prefer to consider the density contrast
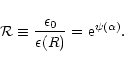 |
(136) |
The density contrast is a monotonous function of  varying from
varying from
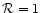 (homogeneous system,
(homogeneous system, 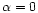 )
to
)
to
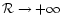 (singular sphere,
(singular sphere,
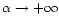 ). It is sometimes of interest to express the results in terms of the redshift (see, e.g., Weinberg 1972)
). It is sometimes of interest to express the results in terms of the redshift (see, e.g., Weinberg 1972)
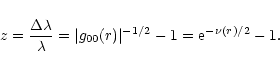 |
(137) |
Using Eq. (126) with the boundary condition (109) at r=R, the redshift of a spectral line emitted from an isothermal sphere is given by
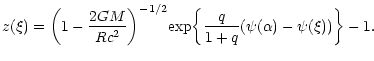 |
|
|
(138) |
3.4 The Milne variables
As in the Newtonian theory, it will be convenient in the following to introduce the Milne variables
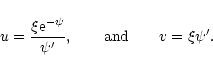 |
(139) |
In terms of these variables, the system of Eqs. (124), (125) can be reduced to a single first order differential equation (Chandrasekhar 1972)
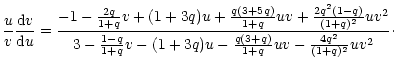 |
|
|
(140) |
For
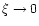 ,
one has
,
one has
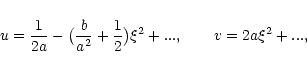 |
(141) |
and for
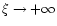
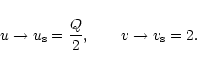 |
(142) |
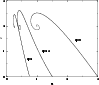 |
Figure 9:
The (u,v) plane for isothermal gaseous spheres in general relativity and for different values of q. The value q=0 corresponds to the Newtonian limit. |
The solution curve in the (u,v) plane is parametrized by 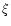 .
Starting from the point
.
Starting from the point
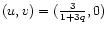 for
for 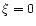 with a slope
with a slope
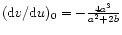 ,
the solution curve spirals indefinitely around the point
,
the solution curve spirals indefinitely around the point
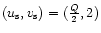 ,
corresponding to the singular sphere, as
,
corresponding to the singular sphere, as
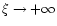 .
All isothermal spheres must necessary lie on this curve (see Fig. 9). For bounded isothermal spheres,
.
All isothermal spheres must necessary lie on this curve (see Fig. 9). For bounded isothermal spheres, 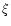 must be terminated at the box radius
must be terminated at the box radius  .
Clearly, the spiral behavior of the (u,v) curve can be ascribed to the oscillating behavior of the solution (134) as
.
Clearly, the spiral behavior of the (u,v) curve can be ascribed to the oscillating behavior of the solution (134) as
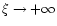 .
An explicit parametric equation for the spiral (valid for
.
An explicit parametric equation for the spiral (valid for
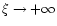 )
can be obtained by substituting the asymptotic expansion (134) in the Milne variables (139) like in the Newtonian case (see Chavanis 2001).
)
can be obtained by substituting the asymptotic expansion (134) in the Milne variables (139) like in the Newtonian case (see Chavanis 2001).
3.5 Oscillatory behavior of the mass-density profile
According to Eq. (123), the relation between the total mass M of the configuration and the central energy density
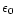 (through the parameter
(through the parameter  )
is given by
)
is given by
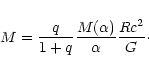 |
(143) |
Solving for 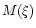 is Eq. (124), we get
is Eq. (124), we get
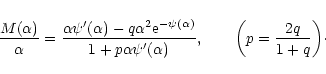 |
(144) |
The relation (143) with Eq. (144) can be expressed very simply in terms of the values of the Milne variables u and v at the normalized box radius  .
Writing
.
Writing
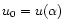 and
and
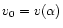 and using Eq. (139), we obtain
and using Eq. (139), we obtain
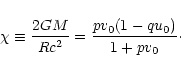 |
(145) |
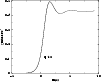 |
Figure 10:
Total mass-energy 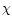 versus central energy density
versus central energy density  for q=1/3.
for q=1/3. |
The curve
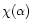 starts from
starts from 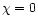 for
for 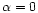 and oscillates around its asymptotic value
and oscillates around its asymptotic value
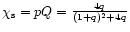 (corresponding to the singular sphere) as
(corresponding to the singular sphere) as
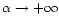 (see Fig. 10). This relation between the total mass and the central density is very similar to the corresponding one for neutron star models (Oppenheimer & Volkoff 1939; Misner & Zapolsky 1964) and dense stellar clusters at statistical equilibrium (Bisnovatyi et al. 1998). In particular, there exists mass peaks in the diagram. In fact, this oscillatory behavior should not cause surprise since the same phenomenon exists for a classical isothermal gas (see in particular Fig. 7 of Chavanis 2001 which can be interpreted as a mass-density relation for a fixed temperature and radius).
(see Fig. 10). This relation between the total mass and the central density is very similar to the corresponding one for neutron star models (Oppenheimer & Volkoff 1939; Misner & Zapolsky 1964) and dense stellar clusters at statistical equilibrium (Bisnovatyi et al. 1998). In particular, there exists mass peaks in the diagram. In fact, this oscillatory behavior should not cause surprise since the same phenomenon exists for a classical isothermal gas (see in particular Fig. 7 of Chavanis 2001 which can be interpreted as a mass-density relation for a fixed temperature and radius).
From Eqs. (143), (144) and (125), one has
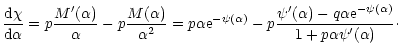 |
|
|
(146) |
In terms of the Milne variables, it can be rewritten
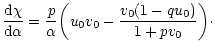 |
|
|
(147) |
Therefore, the extrema of the curve
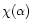 ,
determined by the condition
,
determined by the condition
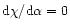 ,
satisfy
,
satisfy
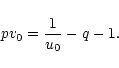 |
(148) |
This equation defines a hyperbole in the (u,v) plane. For
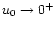 ,
,
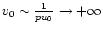 and for
and for
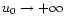 ,
,
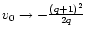 .
The intersections between this curve and the spiral (see Fig. 11) determine the values of
.
The intersections between this curve and the spiral (see Fig. 11) determine the values of  for which
for which 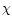 is an extremum. Since the curve (148) passes through the center of the spiral
is an extremum. Since the curve (148) passes through the center of the spiral
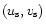 ,
there is an infinity of intersections, resulting in an infinity of oscillations in Fig. 10.
,
there is an infinity of intersections, resulting in an infinity of oscillations in Fig. 10.
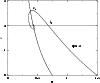 |
Figure 11:
Graphical construction to determine the critical density
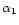 for q=1/3.
for q=1/3. |
The first value
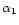 corresponds to the global maximum of
corresponds to the global maximum of 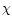 .
Therefore, finite isothermal spheres in general relativity exist only provided that
.
Therefore, finite isothermal spheres in general relativity exist only provided that
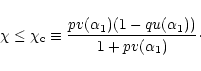 |
(149) |
This implies in particular the existence of a limiting mass (for a given radius R) such that
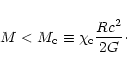 |
(150) |
This result is of course related to the limiting mass of neutron stars discovered by Oppenheimer & Volkoff (1939). In their study, the value of the radius R is determined by a proper modelling of the envelope, instead of an artificial box. However, our results indicate that the essential properties of neutron stars: oscillatory behavior of the mass-density profile, limiting mass and spiral behavior of the mass-radius diagram (see Sect. 3.6) are due primarily to their isothermal core and not to their envelope. Similar observations have been made by Yabushita (1974) who considered the case of an isothermal gaseous sphere surrounded by a medium exerting on it a constant pressure.
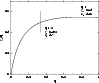 |
Figure 12:
Critical parameter
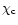 as a function of q. The classical limit
as a function of q. The classical limit
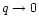 is discussed in Sect. 4.4.
is discussed in Sect. 4.4. |
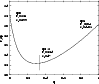 |
Figure 13:
Critical density contrast
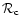 as a function of q.
as a function of q. |
The critical parameter
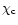 ,
the critical density contrast
,
the critical density contrast
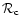 and the critical redshifts
and the critical redshifts 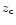 emitted from the center and from the boundary of the isothermal configuration are ploted as a function of q in Figs. 12-14. The corresponding values of
emitted from the center and from the boundary of the isothermal configuration are ploted as a function of q in Figs. 12-14. The corresponding values of
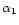 are indicated in Fig. 16 (full line). For the Newtonian case (q=0), we recover the classical values
are indicated in Fig. 16 (full line). For the Newtonian case (q=0), we recover the classical values
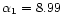 and
and
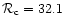 obtained in the canonical ensemble. When q is increased, the critical density
obtained in the canonical ensemble. When q is increased, the critical density
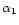 is lowered so that instability occurs sooner than in the Newtonian case. It should be noted, however, that the critical density contrast
is lowered so that instability occurs sooner than in the Newtonian case. It should be noted, however, that the critical density contrast
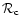 is not a monotonous function of q. This is due to the deformation of the spiral in the (u,v) plane when we vary the relativistic parameter q. We find that the value of q for which
is not a monotonous function of q. This is due to the deformation of the spiral in the (u,v) plane when we vary the relativistic parameter q. We find that the value of q for which
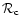 is minimum is close to 1/3, the typical value corresponding to neutron stars. However, the variation of the critical density contrast with q is not very important (
is minimum is close to 1/3, the typical value corresponding to neutron stars. However, the variation of the critical density contrast with q is not very important (
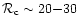 in the whole range of parameters) so that the critical central redshift
in the whole range of parameters) so that the critical central redshift
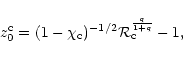 |
(151) |
obtained from Eqs. (138), (136), (145), increases monotonically with q.
 |
Figure 14:
Critical redshifts 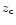 emitted from the center and from the boundary of an isothermal configuration as a function of q.
emitted from the center and from the boundary of an isothermal configuration as a function of q. |
3.6 The mass-radius diagram
It is well-known that, for high central densities, the mass-radius diagram for neutron stars presents a spiral behavior. We show in this section that we can reproduce this behavior within our simple "box'' model. To that purpose, we shall consider configurations with different masses and radii but with the same density
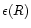 at the boundary of the domain. According to Eqs. (135) and (136), we can express the radius R as a function of the parameter
at the boundary of the domain. According to Eqs. (135) and (136), we can express the radius R as a function of the parameter  by the relation
by the relation
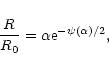 |
(152) |
where we have introduced a typical radius
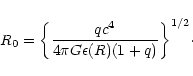 |
(153) |
On the other hand, using Eq. (145), the dimensionless mass appropriate to the present context is given by
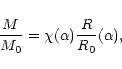 |
(154) |
where
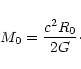 |
(155) |
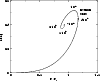 |
Figure 15:
The mass-radius diagram for an isothermal gas with a fixed energy density at the boundary (
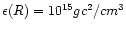 ). We have indicated the value of the central density ). We have indicated the value of the central density
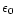 at the turning points.
at the turning points. |
Equations (152), (154) determine the mass-radius relation for an isothermal gas with a fixed energy density at its boundary. The M-R curve, represented in Fig. 15, is parametrized by the central density  .
For comparison with real objects (e.g., neutron stars) we note that the assumption of an isothermal core is valid only for sufficiently large central densities, typically from the point encircled. From that point, our model reproduces qualitatively the spiral behavior of the mass-radius diagram for neutron stars. Using the asymptotic expansion (134) of the function
.
For comparison with real objects (e.g., neutron stars) we note that the assumption of an isothermal core is valid only for sufficiently large central densities, typically from the point encircled. From that point, our model reproduces qualitatively the spiral behavior of the mass-radius diagram for neutron stars. Using the asymptotic expansion (134) of the function 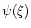 ,
it is possible to determine an explicit equation for the spiral (valid for high densities) in the form
,
it is possible to determine an explicit equation for the spiral (valid for high densities) in the form
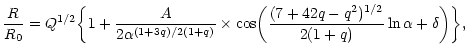 |
|
|
(156) |
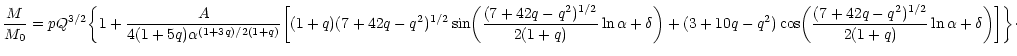 |
|
|
(157) |
In particular, the terminal point of the spiral, corresponding to the singular solution (129), is given by
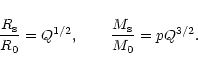 |
(158) |
The previous results are valid for any value of the parameter q. We
shall now specialize on the case of neutron stars for which
q=1/3. For estimating
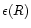 ,
we shall adopt the typical
value given by Misner & Zapolsky (1964)
,
we shall adopt the typical
value given by Misner & Zapolsky (1964)
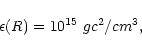 |
(159) |
which corresponds in an ideal neutron gas to a Fermi energy of 130 MeV.
This is the typical value of the energy density in the regime where the kinetic energy of the neutrons is of the same order as their rest mass. This regime corresponds to the transition between the isothermal core and the envelope and it is therefore relevant to adopt this value at r=R. For this density,
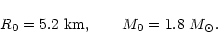 |
(160) |
From the diagram of Fig. 15, we find that the maximum mass and the corresponding radius have the values
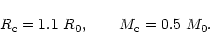 |
(161) |
The value of the maximum mass in our model
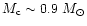 is close to the more exact value
is close to the more exact value 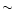 0.7
0.7
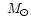 found by Oppenheimer & Volkoff (1939) by introducing a more general equation of state also valid in the envelope. The value of the corresponding radius
found by Oppenheimer & Volkoff (1939) by introducing a more general equation of state also valid in the envelope. The value of the corresponding radius
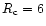 km is slightly smaller than the value
km is slightly smaller than the value 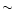 9.6 km usually reported (see, e.g., Weinberg 1972) and the difference in attributed in part to the presence of the envelope which surrounds the isothermal region of size
9.6 km usually reported (see, e.g., Weinberg 1972) and the difference in attributed in part to the presence of the envelope which surrounds the isothermal region of size 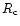 .
According to Eq. (138), the fractional redshift of a spectral line emitted from the edge of the isothermal region (for the configuration of maximum mass) is
.
According to Eq. (138), the fractional redshift of a spectral line emitted from the edge of the isothermal region (for the configuration of maximum mass) is
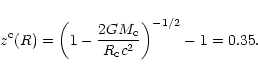 |
(162) |
and the corresponding central redshift
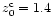 .
Finally, we find that the central density at the mass peak is
.
Finally, we find that the central density at the mass peak is
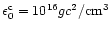 is good agreement with the reference model of Meltzer & Thorne (1966) giving a comparable value. Other central densitites are indicated in Fig. 15. Our curve matches relatively well (qualitatively and semi-quantitatively) the diagram of Meltzer & Thorne (1966) for central densities
is good agreement with the reference model of Meltzer & Thorne (1966) giving a comparable value. Other central densitites are indicated in Fig. 15. Our curve matches relatively well (qualitatively and semi-quantitatively) the diagram of Meltzer & Thorne (1966) for central densities
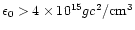 .
.


Up: Gravitational instability of finite
Copyright ESO 2002
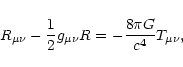
![]() .
Quite generally, the first law of thermodynamics
can be expressed as
.
Quite generally, the first law of thermodynamics
can be expressed as
![]() ). On the other hand, in supermassive stars, temperature and entropy are important but convection keeps the star stired up and produces a uniform entropy distribution (
). On the other hand, in supermassive stars, temperature and entropy are important but convection keeps the star stired up and produces a uniform entropy distribution (![]() const.). In these two important situations, the first law of thermodynamics reduces to
const.). In these two important situations, the first law of thermodynamics reduces to
![]() prevails in a medium where the pressure is entirely due to radiation (Chandrasekhar 1942).
prevails in a medium where the pressure is entirely due to radiation (Chandrasekhar 1942).
![]() ,
,
![]() and
and ![]() by the relations
by the relations
![]() .
In that limit, Eqs. (124), (125) reduce to
.
In that limit, Eqs. (124), (125) reduce to

![]() given by
given by

![]() .
Starting from the point
.
Starting from the point
![]() for
for ![]() with a slope
with a slope
![]() ,
the solution curve spirals indefinitely around the point
,
the solution curve spirals indefinitely around the point
![]() ,
corresponding to the singular sphere, as
,
corresponding to the singular sphere, as
![]() .
All isothermal spheres must necessary lie on this curve (see Fig. 9). For bounded isothermal spheres,
.
All isothermal spheres must necessary lie on this curve (see Fig. 9). For bounded isothermal spheres, ![]() must be terminated at the box radius
must be terminated at the box radius ![]() .
Clearly, the spiral behavior of the (u,v) curve can be ascribed to the oscillating behavior of the solution (134) as
.
Clearly, the spiral behavior of the (u,v) curve can be ascribed to the oscillating behavior of the solution (134) as
![]() .
An explicit parametric equation for the spiral (valid for
.
An explicit parametric equation for the spiral (valid for
![]() )
can be obtained by substituting the asymptotic expansion (134) in the Milne variables (139) like in the Newtonian case (see Chavanis 2001).
)
can be obtained by substituting the asymptotic expansion (134) in the Milne variables (139) like in the Newtonian case (see Chavanis 2001).
![]() (through the parameter
(through the parameter ![]() )
is given by
)
is given by
![]() starts from
starts from ![]() for
for ![]() and oscillates around its asymptotic value
and oscillates around its asymptotic value
![]() (corresponding to the singular sphere) as
(corresponding to the singular sphere) as
![]() (see Fig. 10). This relation between the total mass and the central density is very similar to the corresponding one for neutron star models (Oppenheimer & Volkoff 1939; Misner & Zapolsky 1964) and dense stellar clusters at statistical equilibrium (Bisnovatyi et al. 1998). In particular, there exists mass peaks in the diagram. In fact, this oscillatory behavior should not cause surprise since the same phenomenon exists for a classical isothermal gas (see in particular Fig. 7 of Chavanis 2001 which can be interpreted as a mass-density relation for a fixed temperature and radius).
(see Fig. 10). This relation between the total mass and the central density is very similar to the corresponding one for neutron star models (Oppenheimer & Volkoff 1939; Misner & Zapolsky 1964) and dense stellar clusters at statistical equilibrium (Bisnovatyi et al. 1998). In particular, there exists mass peaks in the diagram. In fact, this oscillatory behavior should not cause surprise since the same phenomenon exists for a classical isothermal gas (see in particular Fig. 7 of Chavanis 2001 which can be interpreted as a mass-density relation for a fixed temperature and radius).
![]() corresponds to the global maximum of
corresponds to the global maximum of ![]() .
Therefore, finite isothermal spheres in general relativity exist only provided that
.
Therefore, finite isothermal spheres in general relativity exist only provided that

![]() ,
the critical density contrast
,
the critical density contrast
![]() and the critical redshifts
and the critical redshifts ![]() emitted from the center and from the boundary of the isothermal configuration are ploted as a function of q in Figs. 12-14. The corresponding values of
emitted from the center and from the boundary of the isothermal configuration are ploted as a function of q in Figs. 12-14. The corresponding values of
![]() are indicated in Fig. 16 (full line). For the Newtonian case (q=0), we recover the classical values
are indicated in Fig. 16 (full line). For the Newtonian case (q=0), we recover the classical values
![]() and
and
![]() obtained in the canonical ensemble. When q is increased, the critical density
obtained in the canonical ensemble. When q is increased, the critical density
![]() is lowered so that instability occurs sooner than in the Newtonian case. It should be noted, however, that the critical density contrast
is lowered so that instability occurs sooner than in the Newtonian case. It should be noted, however, that the critical density contrast
![]() is not a monotonous function of q. This is due to the deformation of the spiral in the (u,v) plane when we vary the relativistic parameter q. We find that the value of q for which
is not a monotonous function of q. This is due to the deformation of the spiral in the (u,v) plane when we vary the relativistic parameter q. We find that the value of q for which
![]() is minimum is close to 1/3, the typical value corresponding to neutron stars. However, the variation of the critical density contrast with q is not very important (
is minimum is close to 1/3, the typical value corresponding to neutron stars. However, the variation of the critical density contrast with q is not very important (
![]() in the whole range of parameters) so that the critical central redshift
in the whole range of parameters) so that the critical central redshift

![]() at the boundary of the domain. According to Eqs. (135) and (136), we can express the radius R as a function of the parameter
at the boundary of the domain. According to Eqs. (135) and (136), we can express the radius R as a function of the parameter ![]() by the relation
by the relation

![]() .
For comparison with real objects (e.g., neutron stars) we note that the assumption of an isothermal core is valid only for sufficiently large central densities, typically from the point encircled. From that point, our model reproduces qualitatively the spiral behavior of the mass-radius diagram for neutron stars. Using the asymptotic expansion (134) of the function
.
For comparison with real objects (e.g., neutron stars) we note that the assumption of an isothermal core is valid only for sufficiently large central densities, typically from the point encircled. From that point, our model reproduces qualitatively the spiral behavior of the mass-radius diagram for neutron stars. Using the asymptotic expansion (134) of the function ![]() ,
it is possible to determine an explicit equation for the spiral (valid for high densities) in the form
,
it is possible to determine an explicit equation for the spiral (valid for high densities) in the form