

Up: Gravitational instability of finite
Subsections
2 Antonov instability for a relativistic gas sphere
2.1 The relativistic gas
We consider a system of N particles, each of mass m, in gravitational interaction. We allow the speed of the particles to be close to the velocity of light so that special relativity must be taken into account. However, in this first approach, we shall treat the gravitational field within the framework of Newtonian mechanics. This procedure is permissible if the typical size of the system is much larger than the Schwarzschild radius (see, e.g., Chandrasekhar 1942). Let
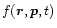 denote the distribution function of the system, i.e.
denote the distribution function of the system, i.e.
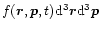 gives the average mass of particles whose positions and momenta are in the cell
gives the average mass of particles whose positions and momenta are in the cell
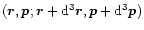 at time t. The integral of f over the momenta determines the spatial density
at time t. The integral of f over the momenta determines the spatial density
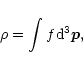 |
(1) |
and the total mass is expressed as
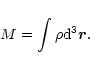 |
(2) |
In a meanfield approximation, the total energy is given by
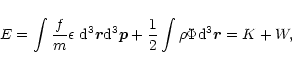 |
(3) |
where K and W are the kinetic and potential energy respectively. According to the theory of special relativity, the energy of a particule reads
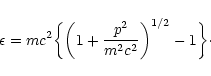 |
(4) |
This expression does not include the rest mass, so it reduces to the usual kinetic energy
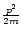 in the Newtonian limit. All the effects of gravity are incorporated in the potential energy which contains the gravitational potential
in the Newtonian limit. All the effects of gravity are incorporated in the potential energy which contains the gravitational potential 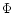 related to the density by the Newton-Poisson equation
related to the density by the Newton-Poisson equation
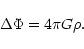 |
(5) |
We now ask which configuration maximizes the Boltzmann entropy
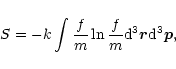 |
(6) |
subject to the conservation of mass M and energy E. To that purpose, we proceed in two steps. In this section, we maximize S[f] at fixed E, M and
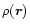 .
This provides an optimal distribution function expressed in terms of
.
This provides an optimal distribution function expressed in terms of 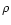 .
Then, in Sect. 2.2, we maximize
.
Then, in Sect. 2.2, we maximize
![$S_{\max}[\rho]$](/articles/aa/full/2002/02/aa1854/img43.gif) at fixed M and E. This optimization problem is not trivial and will be further discussed in Sects. 2.4-2.6.
at fixed M and E. This optimization problem is not trivial and will be further discussed in Sects. 2.4-2.6.
Since the gravitational potential can be deduced from the density by solving the Poisson Eq. (5), maximizing S at fixed E, M and
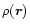 is equivalent to maximizing S at fixed
is equivalent to maximizing S at fixed
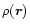 and K. Writing the variational principle in the form
and K. Writing the variational principle in the form
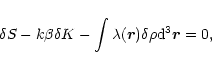 |
(7) |
we obtain the optimal distribution function
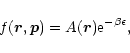 |
(8) |
which is a global entropy maximum with the previous constraints. Equation (8) is the relativistic Maxwell-Boltzmann distribution with an inverse temperature
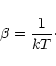 |
(9) |
The Lagrange multipliers
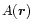 and
and 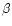 must be related to the constraints
must be related to the constraints
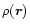 and K. As discussed in detail by Chandrasekhar (1942), these relations can be expressed in terms of the modified Bessel functions
and K. As discussed in detail by Chandrasekhar (1942), these relations can be expressed in terms of the modified Bessel functions
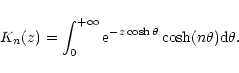 |
(10) |
Using Eqs. (1) (8) (4) and introducing the Juttner transformation
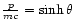 in the integral, the density can be written
in the integral, the density can be written
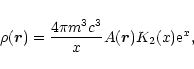 |
(11) |
where we have introduced the dimensionless parameter
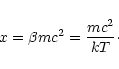 |
(12) |
This parameter quantifies the importance of relativistic effects. The classical limit corresponds to
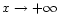 (
(
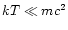 )
and the ultra-relativistic limit to
)
and the ultra-relativistic limit to
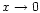 (
(
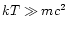 ).
The distribution function (8) can now be expressed in terms of the density as
).
The distribution function (8) can now be expressed in terms of the density as
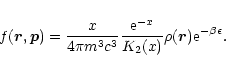 |
(13) |
In the classical limit
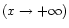 we recover the standard formula
we recover the standard formula
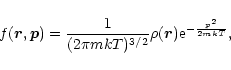 |
(14) |
and in the ultra-relativistic limit (
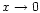 ), we get
), we get
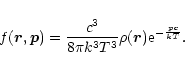 |
(15) |
Similarly, after some elementary transformations, the kinetic energy can be expressed in terms of the normalized inverse temperature x by
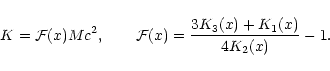 |
(16) |
Using the recursion formula
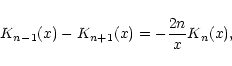 |
(17) |
the function
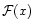 can be written in the equivalent form
can be written in the equivalent form
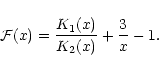 |
(18) |
It has the asymptotic behaviors
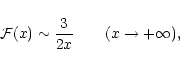 |
(19) |
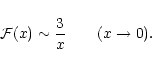 |
(20) |
When substituted in Eq. (16), we recover the usual expressions of the kinetic energy
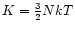 in the classical limit and K=3NkT in the ultra-relativistic limit.
in the classical limit and K=3NkT in the ultra-relativistic limit.
We can now express the entropy in terms of the density 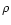 and the inverse temperature x. Substituting the optimal distribution function (13) in Eq. (6), we get, up to an additional constant
and the inverse temperature x. Substituting the optimal distribution function (13) in Eq. (6), we get, up to an additional constant
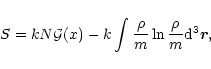 |
(21) |
where
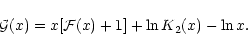 |
(22) |
The function
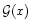 has the asymptotic behaviors
has the asymptotic behaviors
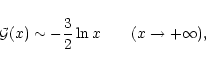 |
(23) |
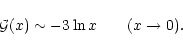 |
(24) |
The thermal contribution to the entropy in the classical limit is
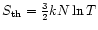 and in the ultra-relativistic limit
and in the ultra-relativistic limit
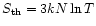 .
.
There exists a general relation between the derivatives of 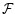 and
and 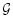 that we shall need in the following. Differentiating Eq. (22) with respect to x and using the identity
that we shall need in the following. Differentiating Eq. (22) with respect to x and using the identity
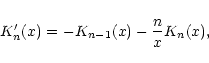 |
(25) |
for n=2, we find that
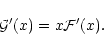 |
(26) |
2.2 First and second order variations of entropy
In the preceding section, we have expressed the entropy and the kinetic energy in terms of the density
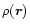 and the temperature T (through the variable x). We now wish to maximize the entropy
and the temperature T (through the variable x). We now wish to maximize the entropy ![$S[\rho]$](/articles/aa/full/2002/02/aa1854/img79.gif) at fixed E and M. For convenience, we shall introduce a new variable
at fixed E and M. For convenience, we shall introduce a new variable
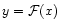 .
In terms of this variable, the total energy and the entropy can be written
.
In terms of this variable, the total energy and the entropy can be written
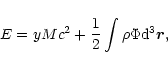 |
(27) |
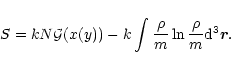 |
(28) |
We can now determine the variations of S around a given density profile
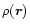 .
To second order in the expansion, we get
.
To second order in the expansion, we get
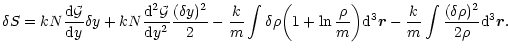 |
|
|
(29) |
Using the identity (26), we find that
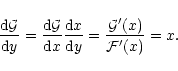 |
(30) |
Differentiating one more time with respect to y, we obtain
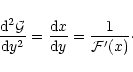 |
(31) |
Substituting the above results in Eq. (29), we get
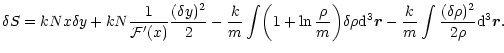 |
|
|
(32) |
We now need to express the variation 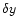 in terms of
in terms of
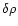 .
From the conservation of energy, we have the exact identity
.
From the conservation of energy, we have the exact identity
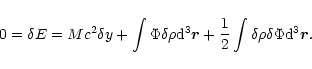 |
(33) |
Substituting the foregoing expression for 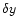 from Eq. (33) in Eq. (32), we obtain
from Eq. (33) in Eq. (32), we obtain
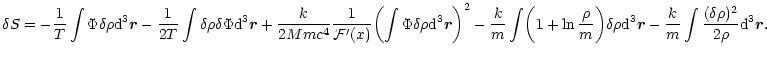 |
|
|
(34) |
Introducing a Lagrange multiplier  to satisfy the conservation of mass, the condition that S is an extremum is written (to first order)
to satisfy the conservation of mass, the condition that S is an extremum is written (to first order)
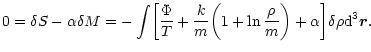 |
|
|
(35) |
This condition must be satisfied for any variations
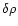 .
This yields the Boltzmann distribution
.
This yields the Boltzmann distribution
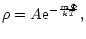 |
|
|
(36) |
like for a classical gas. The condition that the critical point (36) is an entropy maximum requires that
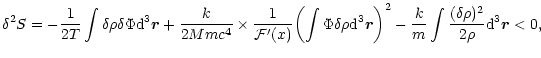 |
|
|
(37) |
for any variation
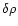 that conserves mass to first order.
that conserves mass to first order.
2.3 The Virial theorem for a relativistic gas
In this section, we derive the form of the Virial theorem appropriate to an isothermal gas described in the framework of special relativity. Quite generally, the potential energy of a self-gravitating system can be expressed in the form (Binney & Tremaine 1987)
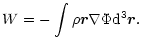 |
|
|
(38) |
If the system is in hydrostatic equilibrium, then
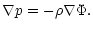 |
|
|
(39) |
Substituting this identity in Eq. (38) and integrating by parts, we get
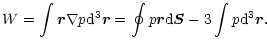 |
|
|
(40) |
If the pressure 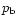 on the boundary of the system is uniform, we can write
on the boundary of the system is uniform, we can write
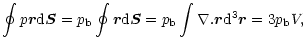 |
|
|
(41) |
where V is the total volume of the system. Therefore, for any system in hydrostatic equilibrium, one has
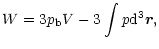 |
|
|
(42) |
which can be considered as the general form of the Virial theorem for self-gravitating systems.
Now, the pressure of an ideal gas can be expressed as (Chandrasekhar 1942)
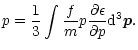 |
|
|
(43) |
For a relativistic gas described by the distribution function (8), we get
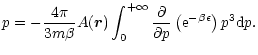 |
|
|
(44) |
Integrating by parts, we obtain
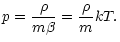 |
|
|
(45) |
Therefore, the equation of state for a (non quantum) relativistic gas is the same as for a classical gas. Written in the form
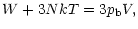 |
|
|
(46) |
the Virial theorem (42) also has the same form as for an isothermal classical gas. However, the Virial theorem is usually expressed in terms of the kinetic energy instead of the temperature. Therefore, the appropriate form of the relativistic Virial theorem reads
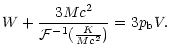 |
|
|
(47) |
In the classical limit (
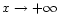 ), it reduces to the well-known formula
), it reduces to the well-known formula
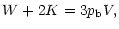 |
|
|
(48) |
and in the ultra-relativistic limit (
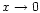 ), we get
), we get
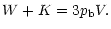 |
|
|
(49) |
It should be emphasized that Eq. (47) is only valid for a relativistic gas in thermal equilibrium.
2.4 The equilibrium phase diagram
Since the equation of state for a relativistic gas is the same as for a classical gas, the equilibrium configurations of such systems correspond to the isothermal gas spheres extensively described in the monograph of Chandrasekhar (1942). Only the onset of the gravitational instability will be modified by relativistic effects.
For non-rotating systems, the equilibrium states are expected to be spherically symmetric. In that case, the Poisson Eq. (5) together with the Boltzmann distribution (36) yield the second order differential equation
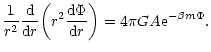 |
|
|
(50) |
This equation can also be deduced from the condition of hydrostatic equilibrium (39) when the pressure is related to the density according to the equation of state (45). It is well-known that the density profile of such isothermal configuations behaves like
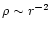 at large distances so that their total mass is infinite. Following Antonov (1962), we shall avoid this infinite mass problem by confining artificially the system within a spherical box of radius R. It is only under this simplifying assumption that a rigorous thermodynamics of self-gravitating systems can be carried out (see, e.g., Padmanabhan 1990; Chavanis et al. 2001). This procedure is justified physically by the realization that a distribution of matter never extends to infinity so R represents an upper cut-off at which other processes intervene to limitate the spatial extent of the system. Of course, different cut-offs are possible but fixing the volume is consistent with the traditional viewpoint of statistical mechanics and it is sufficient to capture the essential physics of the problem (see the different comparisons of truncated models performed by Katz 1980).
at large distances so that their total mass is infinite. Following Antonov (1962), we shall avoid this infinite mass problem by confining artificially the system within a spherical box of radius R. It is only under this simplifying assumption that a rigorous thermodynamics of self-gravitating systems can be carried out (see, e.g., Padmanabhan 1990; Chavanis et al. 2001). This procedure is justified physically by the realization that a distribution of matter never extends to infinity so R represents an upper cut-off at which other processes intervene to limitate the spatial extent of the system. Of course, different cut-offs are possible but fixing the volume is consistent with the traditional viewpoint of statistical mechanics and it is sufficient to capture the essential physics of the problem (see the different comparisons of truncated models performed by Katz 1980).
We now wish to determine the equilibrium phase diagram of a relativistic isothermal gas. To that purpose, we introduce the function
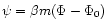 where
where 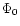 is the gravitational potential at r=0. Then, the density field (36) can be written
is the gravitational potential at r=0. Then, the density field (36) can be written
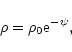 |
(51) |
where 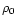 is the central density. Introducing the notation
is the central density. Introducing the notation
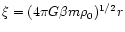 ,
the Boltzmann-Poisson Eq. (50) reduces to the standard Emden form
,
the Boltzmann-Poisson Eq. (50) reduces to the standard Emden form
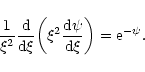 |
(52) |
Equation (52) has a simple analytic solution, the singular sphere
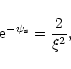 |
(53) |
whose central density is infinite. The regular solution of Eq. (52) satisfying the boundary conditions
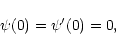 |
(54) |
at the center of the sphere must be computed numerically. In the case of bounded isothermal systems, we must stop the integration at the normalized box radius
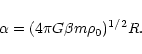 |
(55) |
We shall now relate the parameter  to the
temperature and the energy. According to the Poisson Eq. (5),
we have
to the
temperature and the energy. According to the Poisson Eq. (5),
we have
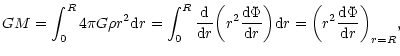 |
|
|
(56) |
which is just a particular case of the Gauss theorem.
Introducing the dimensionless variables defined previously, we get
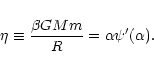 |
(57) |
The relation between  and the normalized temperature
and the normalized temperature 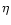 is not affected by special relativity.
is not affected by special relativity.
For the total energy, using the Virial theorem (46) and the expression (16) for the kinetic term, we have
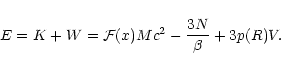 |
(58) |
Now, the pressure at the boundary of the domain can be written
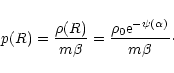 |
(59) |
Expressing the central density in terms of  ,
using Eq. (55), we have equivalently
,
using Eq. (55), we have equivalently
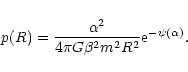 |
(60) |
The total energy therefore reads
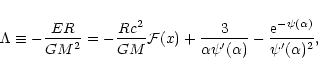 |
(61) |
where we have used Eq. (57) to eliminate the temperature in the last two terms.
It will be convenient in the following to introduce the parameter
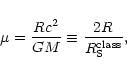 |
(62) |
which is twice the ratio between the system radius R and the "classical'' Schwarzschild radius
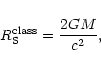 |
(63) |
constructed with the total mass M of the system. Clearly, our
semi-relativistic treatment, which ignores general relativity, is only
valid for 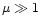 .
However, in our rather formal analysis, we shall
treat
.
However, in our rather formal analysis, we shall
treat 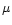 as a free parameter varying in the range
as a free parameter varying in the range
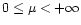 .
The relativistic parameters
.
The relativistic parameters 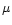 and x are
related to each other by
and x are
related to each other by
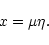 |
(64) |
Therefore, in accordance with Eqs. (61) and (64), the relation between the parameter  and the normalized energy
and the normalized energy 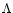 takes
the form
takes
the form
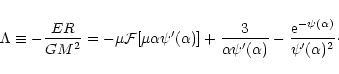 |
(65) |
In the classical limit (
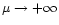 ), we recover the result of Lynden-Bell & Wood (1968)
), we recover the result of Lynden-Bell & Wood (1968)
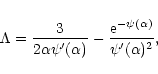 |
(66) |
and in the formal limit
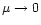 ,
we get
,
we get
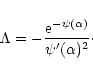 |
(67) |
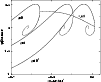 |
Figure 1:
Equilibrium phase diagram for isothermal gas spheres described in the framework of special relativity. Relativistic effects shift the onset of instability to larger energies. |
In Fig. 1, we have represented the equilibrium phase
diagram 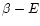 for different values of the relativistic parameter
for different values of the relativistic parameter 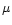 .
We see that the effect of relativity is to shift the spiral to
the left. Therefore, the "gravothermal catastrophe'' (corresponding to
the absence of equilibrium below a critical energy) occurs sooner
than in the Newtonian case. The critical energy is ploted as a
function of the relativistic parameter
.
We see that the effect of relativity is to shift the spiral to
the left. Therefore, the "gravothermal catastrophe'' (corresponding to
the absence of equilibrium below a critical energy) occurs sooner
than in the Newtonian case. The critical energy is ploted as a
function of the relativistic parameter 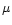 in
Fig. 2. For
in
Fig. 2. For
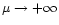 ,
we recover the
classical result of Antonov
,
we recover the
classical result of Antonov
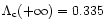 and, in the
formal limit
and, in the
formal limit
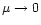 ,
we get
,
we get
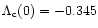 .
Clearly, the spiral is not destroyed by
relativistic effects. Only is its shape slightly modified: the
relativistic spirals are more "stretched'' than the classical
one. Note that the maximum value of
.
Clearly, the spiral is not destroyed by
relativistic effects. Only is its shape slightly modified: the
relativistic spirals are more "stretched'' than the classical
one. Note that the maximum value of 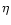 is independant on
is independant on 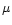 and
is equal to its classical value
and
is equal to its classical value
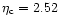 .
On the other hand,
substituting the expression (53) for the singular sphere in
Eqs. (57) and (65), we find that the center of the spiral is
determined by the equations
.
On the other hand,
substituting the expression (53) for the singular sphere in
Eqs. (57) and (65), we find that the center of the spiral is
determined by the equations
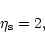 |
(68) |
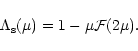 |
(69) |
In the limit
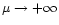 ,
,
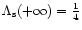 and in the limit
and in the limit
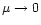 ,
,
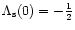 .
.
The spiral is parametrized by the normalized box radius  that goes from 0 (ordinary gas) to
that goes from 0 (ordinary gas) to 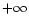 (singular sphere) when
we spiral inwards. If one prefers, we can use a parametrization in
terms of the density contrast
(singular sphere) when
we spiral inwards. If one prefers, we can use a parametrization in
terms of the density contrast
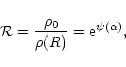 |
(70) |
that goes from 1 to 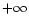 .
In Fig. 3, we plot
the critical density contrast (corresponding to
.
In Fig. 3, we plot
the critical density contrast (corresponding to
 )
as a
function of the relativistic parameter
)
as a
function of the relativistic parameter 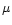 .
For
.
For
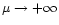 ,
we recover the classical value
,
we recover the classical value
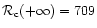 (and
(and
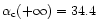 ). For
). For 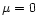 ,
we get
,
we get
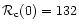 (and
(and
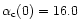 ). It is found that
instability occurs for smaller density contrasts when relativity is accounted for.
). It is found that
instability occurs for smaller density contrasts when relativity is accounted for.
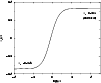 |
Figure 2:
Critical energy
 as a function of the relativistic parameter
as a function of the relativistic parameter 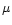 . . |
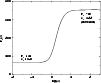 |
Figure 3:
Critical density contrast
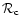 as a function of the relativistic parameter
as a function of the relativistic parameter 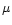 . .
|
2.5 The Milne variables
It will be convenient in the following to introduce the Milne variables (u,v) defined by (Chandrasekhar 1942)
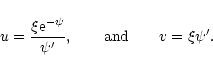 |
(71) |
Taking the logarithmic derivative of u and v with respect to 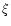 and using Eq. (52), we get
and using Eq. (52), we get
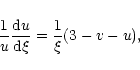 |
(72) |
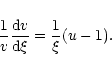 |
(73) |
Taking the ratio of these equations, we find that the variables u and v are related to each other by a first order differential equation
 |
(74) |
The solution curve in the (u,v) plane is well-known and is represented in Fig. 4. Its striking oscillating behavior has been described by a number of authors (see in particular Chandrasekhar 1942). We refer to Padmanabhan (1989) and Chavanis (2001) for the description of its main characteristics in connexion with the present work.
It turns out that the normalized temperature and the normalized energy can be expressed very simply in terms of the values of u and v at the normalized box radius  .
Indeed, writing
.
Indeed, writing
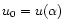 and
and
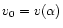 and using Eqs. (57), (65), we get
and using Eqs. (57), (65), we get
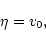 |
(75) |
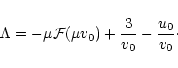 |
(76) |
The intersections between the curves defined by
Eqs. (75), (76) and the spiral in the (u,v) plane
determine the values of  corresponding to a given temperature
or energy. Considering Eq. (75), we find that there is no
intersection for
corresponding to a given temperature
or energy. Considering Eq. (75), we find that there is no
intersection for
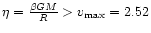 .
Therefore,
below a critical temperature
.
Therefore,
below a critical temperature
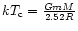 ,
an isothermal
sphere is expected to
collapse. This classical result is not altered by special
relativity. Considering now the microcanonical ensemble, we first note
that Eq. (76) can be rewritten
,
an isothermal
sphere is expected to
collapse. This classical result is not altered by special
relativity. Considering now the microcanonical ensemble, we first note
that Eq. (76) can be rewritten
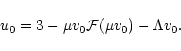 |
(77) |
In the classical limit (
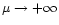 )
it reduces to the straight
line found by Padmanabhan (1989)
)
it reduces to the straight
line found by Padmanabhan (1989)
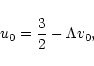 |
(78) |
and in the limit
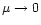 ,
we find another straight line
,
we find another straight line
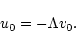 |
(79) |
The curve (77) is ploted in Fig. 4 for a fixed
value of 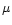 and for different values of
and for different values of 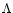 .
For
.
For
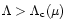 there is no intersection, for
there is no intersection, for
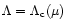 the curve (77) is tangent to the
spiral and for
the curve (77) is tangent to the
spiral and for
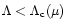 there are one or several
intersections. We recover therefore by this graphical construction the
existence of a critical energy below which no hydrostatic equilibrium
can exist for isothermal spheres. In Fig. 5, we plot the
same diagram as Fig. 4 but for different values of
there are one or several
intersections. We recover therefore by this graphical construction the
existence of a critical energy below which no hydrostatic equilibrium
can exist for isothermal spheres. In Fig. 5, we plot the
same diagram as Fig. 4 but for different values of 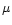 and, in each case, for the critical energy
and, in each case, for the critical energy
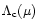 .
The intersection with the spiral determines the value of
.
The intersection with the spiral determines the value of  at the critical point. This
figure confirms that instability occurs sooner (i.e., for smaller values of
at the critical point. This
figure confirms that instability occurs sooner (i.e., for smaller values of  or smaller density contrasts) when relativistic effects are
taken into account.
or smaller density contrasts) when relativistic effects are
taken into account.
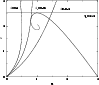 |
Figure 4:
The (u,v) plane. All isothermal spheres must necessarily lie on the spiral. There exists solutions in the canonical ensemble only for 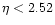 .
In the microcanonical ensemble, the critical energy depends on the relativistic parameter .
In the microcanonical ensemble, the critical energy depends on the relativistic parameter 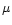 .
For the value .
For the value 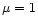 adopted in the figure, there exists solutions only for
adopted in the figure, there exists solutions only for
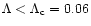 . . |
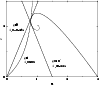 |
Figure 5:
Same as Fig. 4 but for different values of 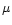 and, in each case, for the critical parameter
and, in each case, for the critical parameter
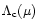 above which there is no equilibrium solution.
above which there is no equilibrium solution. |
2.6 The condition of thermodynamical stability
We now address the question of thermodynamical stability. Let us recall that the isothermal spheres lying on the spirals of Fig. 1 are critical points of entropy but they are not necessarily entropy maxima. To determine whether they are local entropy maxima or saddle points, we must examine the sign of the second variations of entropy given by Eq. (37). In fact, this condition of stability has the same form as in the classical case provided that we make the substitution
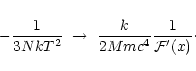 |
(80) |
Therefore, the analysis of Padmanabhan (1989) for the classical Antonov instability can be extended straightforwardly. Introducing the mass perturbation
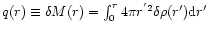 within the sphere of radius r such that
within the sphere of radius r such that
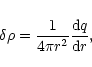 |
(81) |
the second variations of entropy can be put in a quadratic form
 |
(82) |
with
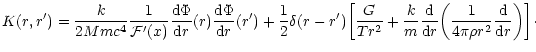 |
|
|
(83) |
Clearly, the conservation of mass imposes the boundary conditions
q(0)=q(R)=0. The problem of stability can therefore be reduced to the study of the eigenvalue equation
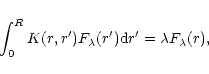 |
(84) |
with the boundary conditions
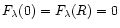 .
If all
the eigenvalues are negative, then
.
If all
the eigenvalues are negative, then
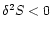 and the critical point
is a local entropy maximum. If one eigenvalue is positive, the
critical point is an unstable saddle point. The point of marginal
stability is determined by the condition that the
largest eigenvalue is equal to zero (
and the critical point
is a local entropy maximum. If one eigenvalue is positive, the
critical point is an unstable saddle point. The point of marginal
stability is determined by the condition that the
largest eigenvalue is equal to zero (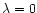 ). We thus have to
solve the differential equation
). We thus have to
solve the differential equation
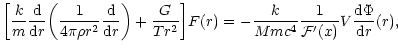 |
|
|
(85) |
with
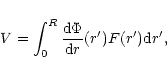 |
(86) |
and
F(0)=F(R)=0. Introducing the dimensionless variables defined in Sect. 2.4, it can be rewritten
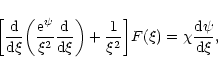 |
(87) |
with
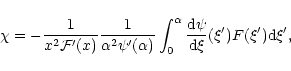 |
(88) |
and
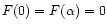 .
As shown by Padmanabhan (1989), the solutions of the differential equation (87) can be expressed in terms of the solutions of the Emden Eq. (52) as
.
As shown by Padmanabhan (1989), the solutions of the differential equation (87) can be expressed in terms of the solutions of the Emden Eq. (52) as
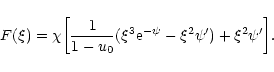 |
(89) |
We can check that this function satisfies the boundary conditions
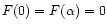 .
The point of marginal stability is obtained by substituting the solution (89) in Eq. (88). The integrations can be carried out and the solutions expressed in terms of the Milne variables u0 and v0 (see Padmanabhan 1989 for more details). In our semi-relativistic treatment, we obtain
.
The point of marginal stability is obtained by substituting the solution (89) in Eq. (88). The integrations can be carried out and the solutions expressed in terms of the Milne variables u0 and v0 (see Padmanabhan 1989 for more details). In our semi-relativistic treatment, we obtain
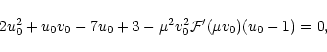 |
(90) |
where we have used Eqs. (64) and (75) to simplify the last term.
In the classical limit
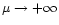 we recover the result of Padmanabhan (1989)
we recover the result of Padmanabhan (1989)
|
4u02+2u0v0-11u0+3=0,
|
(91) |
and in the formal limit
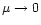 ,
we find
,
we find
The intersections between the curve (90) and the spiral in the (u,v) plane determine the values of  for which a new mode of stability is lost (i.e., a new eigenvalue
for which a new mode of stability is lost (i.e., a new eigenvalue 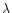 becomes positive). Since the curve (90) passes through the singular sphere
becomes positive). Since the curve (90) passes through the singular sphere
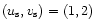 at the center of the spiral, there is an infinity of intersections. The first intersection (for which
at the center of the spiral, there is an infinity of intersections. The first intersection (for which  is minimum) corresponds to the point of marginal stability denoted
is minimum) corresponds to the point of marginal stability denoted
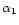 .
We can show that the points determined by Eq. (90) are precisely those for which
.
We can show that the points determined by Eq. (90) are precisely those for which 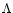 is extremum in agreement with the turning point analysis of Katz (1978). Indeed, differentiating the expression (76) for
is extremum in agreement with the turning point analysis of Katz (1978). Indeed, differentiating the expression (76) for 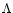 with respect to
with respect to  ,
we get
,
we get
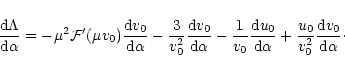 |
(93) |
Using Eqs. (72), (73), we obtain
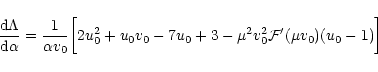 |
(94) |
and we check that the condition
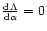 is equivalent to Eq. (90).
is equivalent to Eq. (90).
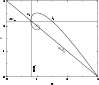 |
Figure 6:
Graphical construction to determine the nodes of the perturbation profile
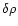 at the point of marginal stability. The construction is done explicitly for
at the point of marginal stability. The construction is done explicitly for 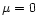 (formally), for which
(formally), for which
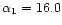 and
u0=0.817. There is only one zero satisfying
and
u0=0.817. There is only one zero satisfying
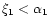 so that the perturbation profile does not present a "core-halo'' structure. This property is maintained until
so that the perturbation profile does not present a "core-halo'' structure. This property is maintained until 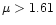 . .
|
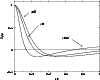 |
Figure 7:
Density perturbation profile at the point of marginal stability as a function of the relativistic parameter. |
It is also easy to determine the form of the perturbation that triggers the instability at the critical point
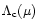 .
According to Eq. (81), the eigenfunction associated with the eigenvalue
.
According to Eq. (81), the eigenfunction associated with the eigenvalue 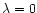 can be written
can be written
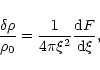 |
(95) |
where 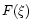 is given by Eq. (89). Simplifying the derivative with the aid of Eq. (52), we can express the perturbation profile in terms of the Milne variables (71) as
is given by Eq. (89). Simplifying the derivative with the aid of Eq. (52), we can express the perturbation profile in terms of the Milne variables (71) as
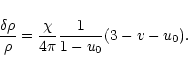 |
(96) |
The qualitative behavior of the perturbation profile can be studied without numerical integration by a graphical construction (see Padmanabhan 1989). The density perturbation
 becomes zero at the point(s)
becomes zero at the point(s)  such that
such that
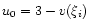 .
In Fig. 6, we first draw the line u=3-v. This line passes through the singular sphere
.
In Fig. 6, we first draw the line u=3-v. This line passes through the singular sphere
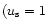 ,
,
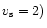 and also cuts the spiral at the points of vertical tangent (see Eq. (72)). In particular, the first intersection corresponds to
and also cuts the spiral at the points of vertical tangent (see Eq. (72)). In particular, the first intersection corresponds to
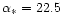 and
(u*,v*)=(0.793,2.208). Then, we draw the line
and
(u*,v*)=(0.793,2.208). Then, we draw the line
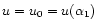 .
The intersection between these two lines determines
.
The intersection between these two lines determines
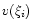 .
The intersection between
.
The intersection between
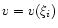 and the spiral determines the zeros of
and the spiral determines the zeros of
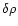 .
For
.
For
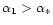 ,
there are two intersections satisfying
,
there are two intersections satisfying
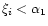 so that the perturbation profile presents a "core-halo'' structure. This is the case in particular in the classical limit
so that the perturbation profile presents a "core-halo'' structure. This is the case in particular in the classical limit
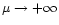 for which
for which
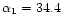 (see Padmanabhan 1989). By contrast, for
(see Padmanabhan 1989). By contrast, for
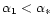 ,
there is only one intersection satisfying
,
there is only one intersection satisfying
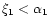 so that the perturbation profile does not present a "core-halo'' structure. This is the case in particular in the (formal) limit
so that the perturbation profile does not present a "core-halo'' structure. This is the case in particular in the (formal) limit 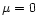 for which
for which
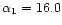 .
The "core-halo'' structure disappears for
.
The "core-halo'' structure disappears for
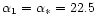 corresponding to a relativistic parameter
corresponding to a relativistic parameter
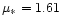 .
Since our study is valid for
.
Since our study is valid for 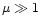 ,
we deduce that the density perturbation profile always presents a "core-halo'' structure in the cases of physical interest. However, relativistic effects have the tendency to reduce the extent of the halo (see Fig. 7).
,
we deduce that the density perturbation profile always presents a "core-halo'' structure in the cases of physical interest. However, relativistic effects have the tendency to reduce the extent of the halo (see Fig. 7).
The previous results are valid in the microcanonical ensemble in which the energy is fixed. In the canonical ensemble, we must consider maxima of the free energy
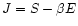 at fixed temperature. In that case, the condition of stability is given by Eq. (85) with V=0. Since the relativistic function
at fixed temperature. In that case, the condition of stability is given by Eq. (85) with V=0. Since the relativistic function
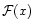 does not appear anymore in the equations, we conclude that special relativity does not change the classical results in the canonical ensemble. In particular, the perturbation profile does not present a "core-halo'' structure at the critical point
does not appear anymore in the equations, we conclude that special relativity does not change the classical results in the canonical ensemble. In particular, the perturbation profile does not present a "core-halo'' structure at the critical point
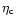 (Chavanis 2001).
(Chavanis 2001).


Up: Gravitational instability of finite
Copyright ESO 2002
![]() denote the distribution function of the system, i.e.
denote the distribution function of the system, i.e.
![]() gives the average mass of particles whose positions and momenta are in the cell
gives the average mass of particles whose positions and momenta are in the cell
![]() at time t. The integral of f over the momenta determines the spatial density
at time t. The integral of f over the momenta determines the spatial density
![]() is equivalent to maximizing S at fixed
is equivalent to maximizing S at fixed
![]() and K. Writing the variational principle in the form
and K. Writing the variational principle in the form
![]() and the inverse temperature x. Substituting the optimal distribution function (13) in Eq. (6), we get, up to an additional constant
and the inverse temperature x. Substituting the optimal distribution function (13) in Eq. (6), we get, up to an additional constant
![]() and
and ![]() that we shall need in the following. Differentiating Eq. (22) with respect to x and using the identity
that we shall need in the following. Differentiating Eq. (22) with respect to x and using the identity
![]() and the temperature T (through the variable x). We now wish to maximize the entropy
and the temperature T (through the variable x). We now wish to maximize the entropy ![]() at fixed E and M. For convenience, we shall introduce a new variable
at fixed E and M. For convenience, we shall introduce a new variable
![]() .
In terms of this variable, the total energy and the entropy can be written
.
In terms of this variable, the total energy and the entropy can be written
![]() where
where ![]() is the gravitational potential at r=0. Then, the density field (36) can be written
is the gravitational potential at r=0. Then, the density field (36) can be written

![]() for different values of the relativistic parameter
for different values of the relativistic parameter ![]() .
We see that the effect of relativity is to shift the spiral to
the left. Therefore, the "gravothermal catastrophe'' (corresponding to
the absence of equilibrium below a critical energy) occurs sooner
than in the Newtonian case. The critical energy is ploted as a
function of the relativistic parameter
.
We see that the effect of relativity is to shift the spiral to
the left. Therefore, the "gravothermal catastrophe'' (corresponding to
the absence of equilibrium below a critical energy) occurs sooner
than in the Newtonian case. The critical energy is ploted as a
function of the relativistic parameter ![]() in
Fig. 2. For
in
Fig. 2. For
![]() ,
we recover the
classical result of Antonov
,
we recover the
classical result of Antonov
![]() and, in the
formal limit
and, in the
formal limit
![]() ,
we get
,
we get
![]() .
Clearly, the spiral is not destroyed by
relativistic effects. Only is its shape slightly modified: the
relativistic spirals are more "stretched'' than the classical
one. Note that the maximum value of
.
Clearly, the spiral is not destroyed by
relativistic effects. Only is its shape slightly modified: the
relativistic spirals are more "stretched'' than the classical
one. Note that the maximum value of ![]() is independant on
is independant on ![]() and
is equal to its classical value
and
is equal to its classical value
![]() .
On the other hand,
substituting the expression (53) for the singular sphere in
Eqs. (57) and (65), we find that the center of the spiral is
determined by the equations
.
On the other hand,
substituting the expression (53) for the singular sphere in
Eqs. (57) and (65), we find that the center of the spiral is
determined by the equations
![]() that goes from 0 (ordinary gas) to
that goes from 0 (ordinary gas) to ![]() (singular sphere) when
we spiral inwards. If one prefers, we can use a parametrization in
terms of the density contrast
(singular sphere) when
we spiral inwards. If one prefers, we can use a parametrization in
terms of the density contrast
![]() .
Indeed, writing
.
Indeed, writing
![]() and
and
![]() and using Eqs. (57), (65), we get
and using Eqs. (57), (65), we get

![]() we recover the result of Padmanabhan (1989)
we recover the result of Padmanabhan (1989)

![]() .
According to Eq. (81), the eigenfunction associated with the eigenvalue
.
According to Eq. (81), the eigenfunction associated with the eigenvalue ![]() can be written
can be written
![]() at fixed temperature. In that case, the condition of stability is given by Eq. (85) with V=0. Since the relativistic function
at fixed temperature. In that case, the condition of stability is given by Eq. (85) with V=0. Since the relativistic function
![]() does not appear anymore in the equations, we conclude that special relativity does not change the classical results in the canonical ensemble. In particular, the perturbation profile does not present a "core-halo'' structure at the critical point
does not appear anymore in the equations, we conclude that special relativity does not change the classical results in the canonical ensemble. In particular, the perturbation profile does not present a "core-halo'' structure at the critical point
![]() (Chavanis 2001).
(Chavanis 2001).