4 Rotational velocities data

4.1 Results

In all, projected rotational velocities were derived for 525 B8 to F2-type stars. Among them, 286 have no rotational velocities either in the compilation of Uesugi & Fukuda (1982) or in Abt & Morrell (1995).

The results of the determinations are presented in Table 4 which contains the following data: Col. 1 gives the HD number, Col. 2 gives the HIP number, Col. 3 displays the spectral type as given in the HIPPARCOS catalogue (ESA 1997), Cols. 4, 5, 6 give respectively the derived value of , the associated standard deviation and the corresponding number of measured lines (uncertain are indicated by a colon), Col. 7 presents possible remarks about the spectra: SB2 ("SB'') and shell ("SH'') natures are indicated for stars detailed in the subsections which follow, as well as the reason why is uncertain - "NO'' for no selected lines, "SS'' for variation from spectrum to spectrum and "LL'' for variation from line to line, as detailed in the Appendix A.

Grenier et al. (1999) studied the same stars with the same spectra and derived radial velocities using cross-correlation techniques. On the basis of the shape of the cross-correlation function (CCF) they find that less than half of the sample has a symmetric and Gaussian CCF and they classify stars with distorted CCF as, among other things, "certain'' "probable'' or "suspected'' doubles.

Uncertainties in are induced by peculiarities in the spectra due for example to binarity or to the presence of a shell. The results for these objects are detailed below. These objects were either known as binaries or newly detected by Grenier et al. (1999).

4.1.1 Binary systems

Spectra of double-lined spectroscopic binary systems (SB2) display lines of both components of the system. They are, by nature, more affected by blends and require much more attention than single stars in order to disentangle both spectra.

Moreover, the difference in radial velocity $\Delta V_{\rm r}$ has to be large enough for the spectrum to show well separated lines. Considering a Gaussian line profile, 98% of the distribution is contained between $\pm 2.326\,\sigma$ ($\sigma$ being the standard deviation of the Gaussian) which is nearly equal to $\pm$FWHM. It follows that a double line resulting from the contribution of the components of a binary system should be spaced of $\vert\Delta\lambda_{\rm A}-\Delta\lambda_{\rm B}\vert \gtrsim 2\,{FWHM}$ (where $\Delta\lambda_{\rm A}$ and $\Delta\lambda_{\rm B}$ are the respective Doppler shifts) to overlap as little as possible and be measurable in terms of determination. Taking the calibration relation from SCBWP as a rule of thumb ( ${FWHM}{\scriptstyle [{\rm\AA}]} \approx 0.025\,\ensuremath{v\sin i} {\scriptstyle [\ensuremath{{\rm km}\,{\rm s}^{-1}} ]}$), the difference of radial velocity in an SB2 system should be higher than:

$$\Delta V_{\rm r} \gtrsim {2\,c\,0.025\over \lambda}\,\ensuremath{v\sin i}\approx 3.4\,\ensuremath{v\sin i} ,$$ (10)

where c is the velocity of light and $\lambda$ the wavelength of the line ($\sim$4350Å). This threshold is a rough estimate of whether is measurable in the case of SB2. On the other hand, the respective cores of the double line cease to be distinct when relative Doppler shift is lower than the FWHM, considering Gaussian profiles, i.e. $\Delta V_{\rm r}\lesssim 1.1\,\ensuremath{v\sin i}$. Below this value, lines of both components merge.

Table 5 displays the results for the stars in our sample which exhibit an SB2 nature. We focus only on stars in which the spectral lines of both component are separated. Spectral lines are identified by comparing the SB2 spectrum with a single star spectrum. Projected rotational velocities are given for each component when measurable, as well as the difference in radial velocity $\Delta V_{\rm r}$ computed from the velocities given by Grenier et al. (1999).

 

 

Table 5: Results of the measurements for individual spectra of SB2 systems. When available, the measurements are given for each component (A for the bluest and B for the reddest). The difference of radial velocity is also given, derived from Grenier et al. Dash (-) indicates a non-determined value: no double-peak CCF for $\Delta V_{\rm r}$ measurement, and $1.1\,\ensuremath{v\sin i}\lesssim\Delta V_{\rm r}\lesssim 3.4\,\ensuremath{v\sin i}$ for individual measurement. When SB2 signature is not detectable a single of merged lines is measured. Last column refers to the corresponding figures.

HD	HIP	Spect. type			$\Delta V_{\rm r}$	Fig.
			( )		( )
			A	B
10167	7649	F0V	17	14	80	12a
			11	13	62	12b
18622	13847	A4III+...	71:	74:	154	13a
			-	-	109	13b
			83		-	13c
27346	19704	A9IV	35	35	135	14a
			36:		-	14b
87330	49319	B9III/IV	11	9	67	15a
			10	10	45	15b
90972	51376	B9/B9.5V	23:	29:	54	15c

• HD 10167 has given no indication of a possible duplicity up to now in the literature and is used as a photometric standard star (Cousins 1974);
• HD 18622 ($\theta^1$ Eri) is a binary system for which HIPPARCOS measured the angular separation $\rho=8\hbox{$.\!\!^{\prime\prime}$ }31\,{\scriptstyle\pm \,0.003}$ and the difference of magnitude $\Delta Hp=1.09\,{\scriptstyle\pm\,0.01}$ of the visual system, while our data concern the SB2 nature of the primary;
• HD 27346 is suspected to be an astrometric binary on the basis of HIPPARCOS observations;
• HD 87330 was detected as a variable star by HIPPARCOS and its variability is possibly due to duplicity;
• HD 90972 ($\delta$ Ant) is a visual double system (Pallavicini et al. 1992) whose primary is an SB2 for which the of both components are given in Table 5. Grenier et al. do not identify $\delta$ Ant as an SB2 system but point to it as a certain double star on the basis of the CCF. It is worth noticing that their CCF is equivalent to a convolution with observed and synthetic spectra and the resulting profile is smoothed by both.

The magnesium doublet is perfectly suited to distinguish a spectral duplicity, so that spectral domain around 4481 Å is displayed for SB2 systems is Figs. 12-15. However, the intrinsic width of the doublet increases its blend due to multiplicity whereas fainter lines can be clearly separated, and Mg II line is not used to derive for SB2 systems.

Less obvious SB2 lie in our sample, but individually analyzing line profiles one-by-one is not an appropriate method for detecting them. Results about binarity for these spectra are however indicated in Grenier et al.

4.1.2 Metallic shell stars

The specific "shell'' feature in stars with a circumstellar envelope is characterized by double emission and central absorption in hydrogen lines. This characteristic is likely a perspective effect, as suggested by (Slettebak 1979), and shell-type lines occur at high inclination i when line of sight intersects with the disk-like envelope. For our purpose, determination, critical effect is due to metallic shell stars, where shell-type absorption not only occurs in Balmer series but also in metallic lines. Our candidate lines exhibit a broad profile, indicating rapid rotation of the central star, a high inclination of the line of sight, and a superimposed sharp absorption profile originating in the circumstellar envelope (Fig. 16). Metallic shell-type lines arise when perspective effect is more marked than for hydrogen shell stars (Briot 1986). Measurement of requires a line profile from the central star photosphere only, and not polluted by absorption caused by the circumstellar envelope which does not reflect the rotation motion.

Figure 12: The part of the spectrum of HD 10167, centered around Mg II 4481 (4460-4500Å) is displayed for the two observed spectra of the star. Both panels present the binarity. Relative radial velocities are high enough compared to rotational broadening to allow to measure for both components. Observation b) occurs nearly two years after observation a).

Figure 13: HD 18622 has been observed at three different times: a) HJD 2447790, b) 2448525 and c) 2448584. For each spectrum the region around Mg II 4481Å is displayed. Relative radial velocities vary from about indiscernible components in panel c) to nearly 150 in a). Relatively high rotational broadening makes the measurement of difficult because of the ratio $\Delta V_{\rm r}\over\ensuremath{v\sin i}$, and derived rotational velocities are uncertain.

Figure 14: HD 27346 spectra have been collected at two different orbital phases separated in time by 981 days. Mg II line shows clearly the two components in panel a), whereas they are merged in b).

Figure 15: a) and b) Observations of HD 87330 around Mg II, separated by almost three years. Low rotational broadening allows the measurement of using weak metallic lines, whereas Mg II line of both components overlap, due to the intrinsic width of the doublet. c) Spectrum of the late B star HD 90972, with few metallic lines. The low difference of radial velocities makes the measurement of uncertain.

Figure 16: Part of the spectrum of HD 225200 showing the rotationally broadened line Mg II 4481 (filled circle) and metallic lines exhibiting the signature of the shell as sharp core and extended wings (open triangle).

Derived for the metallic shell stars present in our sample are listed in Table 6. These stars are already known as shell stars. HD 15004 (71 Cet) and HD 225200 are further detailed by Gerbaldi et al. In our spectral range, magnesium multiplet Mg II 4481 is the only measurable line.

 

 

Table 6: Results of the measurements for individual spectra of metallic shell stars.

HD	HIP	Spectral type
			( )
15004	11261	A0III	249
24863	18275	A4V	249
38090	26865	A2/A3V	204
88195	49812	A1V	236
99022	55581	A4:p	236
			236
			249
225200	345	A1V	345

   
4.2 Comparison with existing data

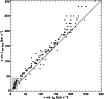Figure 17: Comparison between values from this work and from Abt & Morrell (1995, AM) for the 160 common stars. The solid line stands for the one-to-one relation. The grey box encompasses the points of low , for which the relation has a much higher local slope and produces an overestimation of the global slope.

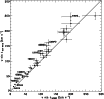Figure 18: Comparison between data from this work and from Slettebak et al. The solid line stands for the one-to-one relation. The 35 standard stars are plotted with error bar on both axes (see text). The stars that deviate most from the one-to-one relation have their HD number indicated and are summarized in Table 7.

The most homogeneous large data set of rotational velocities for A-type stars which has been provided up to now is that of AM (1995), who measured for about 1700 A-type stars in the northern hemisphere. The intersection with our southern sample includes 160 stars. The comparison of the (Fig. 17) shows that our determination is higher on average than the velocities derived by Abt & Morrell (AM). The linear relation given by GaussFit is:

$$\ensuremath{v\sin i} _{\rm this\;work} = 1.15\,{\scriptstyle... ...\,\ensuremath{v\sin i} _{\rm AM}+2.1\,{\scriptstyle\pm\, 0.8}.$$ (11)

Abt & Morrell based their measurements on the scale established by SCBWP, who built a new calibration FWHM- , replacing the old system and leading to values 5% smaller on average for A-F stars.

There are 35 stars in common between our sample and the standard stars of SCBWP. It is worth emphasizing that among these 35 stars, only one third has a Gaussian CCF in the study of Grenier et al. Moreover there is an SB2 system (HD 18622) and almost one half of this group is composed of suspected or probable multiple stars, on the basis of their CCF.

Figure 18 displays the derived in this paper versus the from SCBWP for the 35 standard stars in common. The solid line represents the one-to-one relation. A clear trend is observed: from SCBWP are on average 10 to 12% lower. A linear least squares fit carried out with GaussFit on these values makes the systematic effect explicit:

$$\ensuremath{v\sin i} _{\rm this\;work} = 1.04\,{\scriptstyle... ...ensuremath{v\sin i} _{\rm SCBWP}+6.1\,{\scriptstyle\pm \,1.0}.$$ (12)

The relation is computed taking into account the error bars of both sources. The error bars on the values of SCBWP are assigned according to the accuracy given in their paper (10% for $\ensuremath{v\sin i} <200\,\ensuremath{{\rm km}\,{\rm s}^{-1}}$ and 15% for $\ensuremath{v\sin i}\geq 200\,\ensuremath{{\rm km}\,{\rm s}^{-1}}$). Our error bars are derived from the formal error found in Sect. 3.5 (Eq. (9)).

The difference between the two relations, Eq. (11) and Eq. (12), concerns mainly the low region. When low from Abt & Morrell <25  , are not taken into account (grey box in Fig. 17), the relation given by GaussFit between from Abt & Morrell and this work becomes:

$$\ensuremath{v\sin i} _{\rm this\;work} = 1.08\,{\scriptstyle... ...\,\ensuremath{v\sin i} _{\rm AM}+5.3\,{\scriptstyle\pm \,1.8},$$ (13)

which is almost identical to the relation with SCBWP data (Eq. (12)).

 

 

Table 7: Highlight of the discrepancy between values from SCBWP and ours (standard deviation of our measurement is indicated; dash "-'' stands for only one measurement). Comparison with data from the literature for the twelve stars that exhibit the largest differences. are classified in three subgroups according to the way they are derived: by-product of a spectrum synthesis, frequency analysis of the lines profiles or infered from a FWHM- relation independent from SCBWP's one. Flags from HIPPARCOS catalogue are indicated: variability flag H52 (C: constant, D: duplicity-induced variability, M: possibly micro-variable, U: unsolved variable, -: no certain classification) and double annex flag H59 (O: orbital solution, G: acceleration terms, -: no entry in the Double and Multiple Systems Annex). The shape of the CCF found by Grenier et al. is also given (0: symmetric and Gaussian peak, 1: SB2, 2: certain double, near spectral types, 3: certain double, A-B type with faint F-G component, 4: probable double, 5: suspected double, 6: probable multiple system, 7: certain shell star, 8: suspected shell star, 9: wide and irregular peak, 10: wide peak of B star (few lines)).

Name	HD	Sp. type	( )						HIPPARCOS		CFF
$\nu$ Pup	47670	B8III	200	246	${\scriptstyle\pm \,7}$	-	-	-	U	-	5
$\alpha$ CMa	48915	A0m...	10	16	${\scriptstyle\pm \,1}$	$16\,{\scriptstyle\pm\, 1}^{(1)}\;16^{(2)}$	$17^{(4)}\;16.9^{(5)}$	-	-	-	0
						16.2(3)	$19^{(6)}\;15.3\,{\scriptstyle\pm\, 0.3}^{(7)}$
QW Pup	55892	F0IV	40	51	${\scriptstyle\pm\, 8}$	-	-	50(8)	M	-	4
a Vel	75063	A1III	20	30	${\scriptstyle\pm\, 2}$	-	-	-	-	-	0
$\alpha$ Vol	78045	Am	25	34	${\scriptstyle\pm\, 2}$	45(9)	-	-	C	-	0
$\theta$ Leo	97633	A2V	15	23	${\scriptstyle\pm \,1}$	$21^{(2)}\;22.1^{(3)}$	-	23(10)	-	-	0
A Cen	100673	B9V	125	160	-	-	-	-	C	-	10
$\lambda$ Mus	102249	A7III	50	60	${\scriptstyle\pm\, 2}$	-	-	60(11)	C	O	0
$\psi$ Cen	125473	A0IV	100	124	${\scriptstyle\pm\, 2}$	132(9)	-	-	-	-	5
$\epsilon$ Aqr	198001	A1V	85	102	-	$108.1^{(3)}\;95^{(12)}$	-	-	-	-	0
$\omega^2$ Aqr	222661	B9V	120	150	-	-	-	-	C	-	4

(1) Kurucz et al. (1977).	(5) Deeming (1977).	(9) Holweger et al. (1999).
(2) Lemke (1989).	(6) Ramella et al. (1989).	(10) Fekel (1998).
(3) Hill (1995).	(7) Dravins et al. (1990).	(11) Noci et al. (1984).
(4) Smith (1976).	(8) Balachandran (1990).	(12) Dunkin et al. (1997).

For slow rotational velocities, the discrepancy far exceeds the estimate of observational errors. Figure 18 also shows the stars which deviate the most from the one-to-one relation. These twelve stars, for which the error box around the point does not intersect with the one-to-one relation, are listed in Table 7 with different rotational velocity determinations gathered from the literature. Their large differences together with comparison to other data allow us to settle on which source carries the systematic effect. Without exception, all data gathered from the literature and listed in Table 7 are systematically higher than the corresponding SCBWP's and for the majority of the listed stars, data from the literature are consistent with our determinations. These stars are further detailed in the Appendix B.