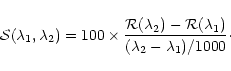Up: BVRI Photometry of 27 Telescope
Subsections
5 Results
Table 3:
Absolute magnitude and colors for all objects, obtained from the photometric measurements presented in Table 2. For objects measured during both runs, we present one value per run, in order to highlight any instrinsic change.
| Object |
(1) |
(2) |
M(1,1)
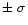 |
RN [km] |
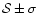 |
B-V
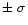 |
V-R
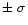 |
R-I
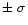 |
| |
|
|
|
|
|
|
|
|
| 1993 SB |
Plut |
2b |
8.07  0.08
0.08 |
65.5  2.4
2.4 |
13.31  3.78
3.78 |
0.76  0.10
0.10 |
0.48  0.07
0.07 |
0.53  0.08
0.08 |
| 1994 TB |
Plut |
1b |
7.32  0.05
0.05 |
92.5  2.5
2.5 |
44.89  3.26
3.26 |
1.10  0.07
0.07 |
0.78  0.06
0.06 |
0.72  0.08
0.08 |
| |
|
2b |
7.59  0.09
0.09 |
81.8  3.6
3.6 |
28.12  4.73
4.73 |
1.04  0.12
0.12 |
0.60  0.08
0.08 |
0.70  0.12
0.12 |
| 1995 SM55 |
QB1 |
1b |
4.39  0.02
0.02 |
356.9  4.4
4.4 |
0.27  1.92
1.92 |
0.65  0.02
0.02 |
0.38  0.03
0.03 |
0.29  0.04
0.04 |
| |
|
2a |
4.32  0.06
0.06 |
368.0  10.2
10.2 |
-1.14  3.58
3.58 |
0.63  0.06
0.06 |
0.33  0.06
0.06 |
0.35  0.09
0.09 |
| 1995 TL8 |
Scat |
2b |
4.58  0.06
0.06 |
325.8  9.0
9.0 |
33.94  3.05
3.05 |
1.04  0.07
0.07 |
0.69  0.05
0.05 |
0.64  0.08
0.08 |
| 1996 RQ20 |
QB1 |
1a |
6.89  0.10
0.10 |
112.4  5.7
5.7 |
23.16  4.97
4.97 |
0.95  0.14
0.14 |
0.61  0.09
0.09 |
0.55  0.12
0.12 |
| 1997 QH4 |
QB1 |
2b |
7.19  0.13
0.13 |
98.2  6.4
6.4 |
20.81  6.34
6.34 |
1.10  0.17
0.17 |
0.52  0.11
0.11 |
0.66  0.16
0.16 |
| 1997 QJ4 |
Plut |
1b |
7.29  0.12
0.12 |
93.6  5.3
5.3 |
6.89  5.63
5.63 |
-- |
0.45  0.12
0.12 |
0.40  0.10
0.10 |
| 1998 BU48 |
Scat |
2a |
7.03  0.06
0.06 |
105.5  3.0
3.0 |
26.98  3.10
3.10 |
1.10  0.07
0.07 |
0.65  0.05
0.05 |
0.57  0.08
0.08 |
| 1998 SG35 |
Cent |
1b |
10.83  0.02
0.02 |
18.4  0.2
0.2 |
12.11  1.67
1.67 |
0.69  0.02
0.02 |
0.46  0.03
0.03 |
0.52  0.04
0.04 |
| 1998 SM165 |
QB1 |
2a |
5.91  0.05
0.05 |
176.6  4.7
4.7 |
29.72  2.94
2.94 |
0.94  0.07
0.07 |
0.64  0.05
0.05 |
0.65  0.07
0.07 |
| 1998 SN165 |
QB1 |
1b |
5.44  0.09
0.09 |
220.0  9.9
9.9 |
7.83  4.78
4.78 |
0.56  0.12
0.12 |
0.50  0.09
0.09 |
0.34  0.11
0.11 |
| 1998 TF35 |
Cent |
2a |
8.51  0.07
0.07 |
53.4  1.8
1.8 |
36.67  3.79
3.79 |
1.13  0.08
0.08 |
0.68  0.07
0.07 |
0.72  0.09
0.09 |
| 1998 UR43 |
Plut |
2a |
7.94  0.08
0.08 |
69.4  2.7
2.7 |
5.73  4.66
4.66 |
0.78  0.10
0.10 |
0.49  0.08
0.08 |
0.27  0.12
0.12 |
| 1998 WH24 |
QB1 |
2b |
4.43  0.06
0.06 |
350.0  10.5
10.5 |
22.61  3.29
3.29 |
1.01  0.08
0.08 |
0.58  0.05
0.05 |
0.59  0.08
0.08 |
| 1998 WV31 |
Plut |
2b |
7.64  0.07
0.07 |
79.7  2.7
2.7 |
10.20  4.28
4.28 |
0.83  0.09
0.09 |
0.51  0.07
0.07 |
0.36  0.11
0.11 |
| 1998 WX31 |
QB1 |
2a |
6.22  0.07
0.07 |
153.1  5.6
5.6 |
26.20  4.61
4.61 |
-- |
0.60  0.08
0.08 |
0.64  0.11
0.11 |
| 1999 CC158 |
Scat |
2a |
5.43  0.07
0.07 |
220.7  8.0
8.0 |
20.29  3.66
3.66 |
0.96  0.10
0.10 |
0.57  0.06
0.06 |
0.55  0.09
0.09 |
| 1999 CD158 |
QB1 |
2b |
4.90  0.07
0.07 |
281.4  9.1
9.1 |
13.43  3.73
3.73 |
0.87  0.08
0.08 |
0.48  0.06
0.06 |
0.54  0.09
0.09 |
| 1999 CF119 |
Scat |
2b |
7.03  0.08
0.08 |
105.6  4.0
4.0 |
13.45  4.60
4.60 |
-- |
0.56  0.08
0.08 |
0.39  0.11
0.11 |
| 1999 DE9 |
Scat |
2b |
4.88  0.06
0.06 |
284.4  8.0
8.0 |
20.77  3.37
3.37 |
0.86  0.07
0.07 |
0.58  0.06
0.06 |
0.56  0.08
0.08 |
| 1999 OX3 |
Scat |
1a |
6.97  0.22
0.22 |
108.8  11.5
11.5 |
-- |
-- |
-- |
0.47  0.11
0.11 |
| 1999 RZ253 |
QB1 |
1b |
5.43  0.06
0.06 |
284.4  7.8
7.8 |
29.96  3.00
3.00 |
-- |
0.65  0.06
0.06 |
0.65  0.06
0.06 |
| 1999 TC36 |
Plut |
1b |
4.83  0.03
0.03 |
290.5  4.3
4.3 |
31.69  1.70
1.70 |
1.03  0.04
0.04 |
0.68  0.03
0.03 |
0.63  0.03
0.03 |
| |
|
2b |
4.88  0.05
0.05 |
285.0  6.6
6.6 |
33.51  2.64
2.64 |
1.03  0.06
0.06 |
0.70  0.04
0.04 |
0.61  0.07
0.07 |
| 1999 TD10 |
Scat |
1b |
8.71  0.02
0.02 |
48.8  0.5
0.5 |
12.83  1.50
1.50 |
-- |
0.51  0.03
0.03 |
0.47  0.03
0.03 |
| 1999 UG5 |
Cent |
2a |
10.09  0.04
0.04 |
25.8  0.6
0.6 |
28.82  2.58
2.58 |
0.97  0.05
0.05 |
0.65  0.04
0.04 |
0.60  0.07
0.07 |
| 2000 OK67 |
QB1 |
2a |
6.14  0.06
0.06 |
159.3  4.9
4.9 |
-- |
-- |
0.52  0.07
0.07 |
-- |
| |
|
2b |
-- |
159.3  4.9
4.9 |
-- |
0.73  0.11
0.11 |
-- |
-- |
| |
|
(*) |
6.14  0.06
0.06 |
159.3  4.9
4.9 |
15.97  7.06
7.06 |
0.73  0.11
0.11 |
0.52  0.07
0.07 |
-- |
| 2000 QC243 |
QB1 |
2a |
7.95  0.05
0.05 |
69.2  1.7
1.7 |
6.96  2.72
2.72 |
0.72  0.06
0.06 |
0.45  0.04
0.04 |
0.40  0.07
0.07 |
(1) class: QB1 = Cubewano, Plut = Plutino, Scat = Scaterred Disk Object, Cent = Centaur. (2) run (UT date): 1a = 2000 Sep. 04, 1b = 2000 Sep. 05, 2a = 2000 Nov. 29, 2b = 2000 Nov. 30 (*) = compilation of Run 2a & 2b. M11 is the absolute R magnitude. RN is an estimation of the radius of the object (in km) given by Eq. (2). 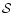 is the spectral gradient in (%/100 nm) as defined in the text.
is the spectral gradient in (%/100 nm) as defined in the text.
|
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Delsanti1904f1.eps}\hspace...
...hspace*{4mm}
\includegraphics[width=7.5cm,clip]{Delsanti1904f6.eps}
\end{figure}](/articles/aa/full/2001/46/aa1904/Timg6.gif) |
Figure 1:
Color-color
diagrams for the 27 objects. The meaning of the different symbols is
given in the middle right panel. The reddening line (which is the
locus of objects displaying a linear reflectivity spectrum) has a
range of gradients 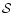 from -10 to 70%/100 nm; a tick mark
is placed at every 10 units.
from -10 to 70%/100 nm; a tick mark
is placed at every 10 units. |
The resulting color indexes computed from the classical photometry
measurements are shown in Table 3. For objects that
have been measured at different epochs, we present one value per epoch
in order to monitor any intrinsic brightness variation between the two
runs. For objects which have repeated R measurements during the same
night of observation, the colors are obtained from the average R.
The absolute magnitude M(1,1) has been computed for each epoch. It is
defined as:
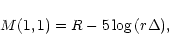 |
(1) |
where R is the R magnitude, r and 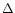 are respectively the
helio- and geocentric distances [AU] at the time of the
observations. We do not take into account the phase correction
are respectively the
helio- and geocentric distances [AU] at the time of the
observations. We do not take into account the phase correction
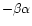 , where
, where 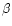 is the phase coefficient (cf. Meech & Jewitt 1987 and Delahodde et al. 2001 for values of phase
coefficient; a typical value is
is the phase coefficient (cf. Meech & Jewitt 1987 and Delahodde et al. 2001 for values of phase
coefficient; a typical value is 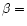 0.04 mag/
0.04 mag/
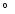 ), and
), and 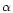 is the phase angle. Indeed, M(1,1) is used in this paper only for a
rough estimation of the radius of the object, whose error is dominated
by the albedo uncertainty.
is the phase angle. Indeed, M(1,1) is used in this paper only for a
rough estimation of the radius of the object, whose error is dominated
by the albedo uncertainty.
As for color indexes, for objects with
several epochs available, we present one value of the M(1,1)obtained per epoch. In this way, we can improve our interpretation of
any brightening or change between two epochs.
Assuming a canonical surface albedo of p=0.04 (corresponding to
that of cometary nuclei, Keller 1990), we can estimate the radius
RN[km] of each object. This value of the albedo is in agreement with
thermal IR measurements obtained for TNOs by Thomas et al. (2000).
RN[km] is computed with the following formula (Russell 1916):
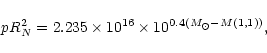 |
(2) |
where 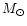 is the R magnitude of the Sun, M(1,1) is the
absolute R magnitude from Eq. (1) and p is the albedo.
The values obtained are also presented in Table 3.
is the R magnitude of the Sun, M(1,1) is the
absolute R magnitude from Eq. (1) and p is the albedo.
The values obtained are also presented in Table 3.
It is interesting to note that this radius, evaluated assuming an
albedo p=0.04, can be in error by a factor of 2 or more because of
the uncertainty of this albedo. This is especially true for bluish
objects, whose albedo could be fairly high (in the case of a
fresh ice surface, i.e. 0.1 for Chiron, Hartmann et al. 1981), or very low
(in the order of 0.02 in case of highly irradiated objects; Thompson et al. 1987). Therefore, this estimation of the radius has to be taken with precaution.
5.4 Spectral gradient
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Delsanti1904f10.eps}\hspace*{4mm}
\includegraphics[width=8.8cm,clip]{Delsanti1904f11.eps}
\end{figure}](/articles/aa/full/2001/46/aa1904/Timg19.gif) |
Figure 2:
Reflectivity spectra. The
reflectivity is normalized to 1 for the V filter; the "spectra'' have
been arbitrarily shifted for clarity. For each object, the dotted
line is the linear regression over the V, R, I range (excluding B), corresponding to
the gradient 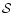 reported in this paper.
reported in this paper. |
The color indexes can also be converted into relative spectral
reflectivities
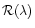 ,
computed at the central wavelength
of the broadband filters used (Jewitt & Meech 1986). We normalized these
reflectivities at the central wavelength of the V filter, leading to
the following equation:
,
computed at the central wavelength
of the broadband filters used (Jewitt & Meech 1986). We normalized these
reflectivities at the central wavelength of the V filter, leading to
the following equation:
![\begin{displaymath}
%
{\cal R}(\lambda) = 10^{-0.4[ (m(\lambda)-m(V)) - (m(\lambda)-m(V))_\odot]},
\end{displaymath}](/articles/aa/full/2001/46/aa1904/img21.gif) |
(3) |
where m and 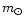 are the magnitude of the object and of the Sun
at the appropriate wavelength. In other words, the color indices are
equivalent to very low resolution spectra. These spectra are presented
in Fig. 2. To characterize a reflectivity spectrum, we
can consider the reddening,
are the magnitude of the object and of the Sun
at the appropriate wavelength. In other words, the color indices are
equivalent to very low resolution spectra. These spectra are presented
in Fig. 2. To characterize a reflectivity spectrum, we
can consider the reddening, 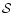 (also called the slope
parameter or spectral index, cf. Hainaut & Delsanti 2001), defined as percent
of reddening per 100 nm as:
(also called the slope
parameter or spectral index, cf. Hainaut & Delsanti 2001), defined as percent
of reddening per 100 nm as:
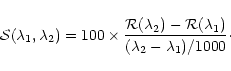 |
(4) |
As most objects have a linear reflectivity spectrum over the V, R, and
I bands, we can compute the mean reddening, 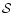 ,
by linear
regression. All the values are presented in
Table 3.
,
by linear
regression. All the values are presented in
Table 3.
On each color-color plot we have represented a line which characterizes the locus of objects with a
linear reflectivity spectrum, with reddening (i.e. spectral slope) ranging from -10 < 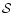 < 70
< 70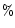 /100 nm, to guide the eye.
/100 nm, to guide the eye.


Up: BVRI Photometry of 27 Telescope
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{Delsanti1904f1.eps}\hspace...
...hspace*{4mm}
\includegraphics[width=7.5cm,clip]{Delsanti1904f6.eps}
\end{figure}](/articles/aa/full/2001/46/aa1904/Timg6.gif)
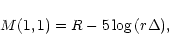
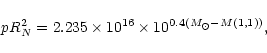
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Delsanti1904f10.eps}\hspace*{4mm}
\includegraphics[width=8.8cm,clip]{Delsanti1904f11.eps}
\end{figure}](/articles/aa/full/2001/46/aa1904/Timg19.gif)
![\begin{displaymath}
%
{\cal R}(\lambda) = 10^{-0.4[ (m(\lambda)-m(V)) - (m(\lambda)-m(V))_\odot]},
\end{displaymath}](/articles/aa/full/2001/46/aa1904/img21.gif)