| Parameter | Value |
| SFR | Extended burst,
|
| 1+x | 2.00 |
|
|
120 |
| Age (Myr) | 3.0 |
| Z | 0.004 |
|
|
|
In this section, we will compare the kinetic luminosity of NGC 2363 to the heating rate implied by the observed temperature fluctuations. To estimate the kinetic luminosity produced by the stellar winds in NGC 2363, we considered a synthetic stellar population with the parameters resumed in Table 1. The only difference with respect to the model by Luridiana et al. (1999) is the adoption of Z=0.004 instead of Z=0.005, to avoid interpolation between spectra, and to allow a more direct comparison with the models by Binette & Luridiana (2000). This choice has little influence on the temperature-fluctuation problem, since we estimate that adopting Z=0.005 would increase the kinetic luminosity by less than 50% (Leitherer et al. 1992), which is not sufficient to change, as we will see, the results of this work.
| Parameter | Value |
| SFR | Extended burst,
|
| 1+x | 2.00 |
|
|
120 |
| Age (Myr) | 3.0 |
| Z | 0.004 |
|
|
|
Three different estimates of the kinetic luminosity
![]() and the total integrated wind energy for this source are listed
in Table 2.
One of them was obtained with the first release of Starburst99 (see Leitherer et al. 1999)
run with a theoretical wind treatment,
which is the default set by the code and the one preferred by the
authors of Starburst99.
The other two were obtained
with an updated version of the synthesis code of Cerviño & Mas-Hesse (1994) (hereafter CMHK, see Cerviño et al. 2001a for details),
with the wind treatment illustrated in Cerviño et al. (2001a).
The reasons for considering two different synthesis codes with two different mass-loss laws
reside in the importance of showing the effects of
different assumptions on the wind treatment
(a possibility granted by the Starburst99 code,
which can be set to any of four different laws),
together with the importance of estimating the expected statistical dispersion
in the energy-related quantitities (a possibility granted by the CMHK code,
either analytically or by means of Monte Carlo simulations).
Stated otherwise, it is not our intention to compare the two codes, but rather the two wind treatments:
had we chosen the same one as Cerviño et al. (2001a) in the Starburst99 settings, we would have found the same result as
with the CMHK code.
and the total integrated wind energy for this source are listed
in Table 2.
One of them was obtained with the first release of Starburst99 (see Leitherer et al. 1999)
run with a theoretical wind treatment,
which is the default set by the code and the one preferred by the
authors of Starburst99.
The other two were obtained
with an updated version of the synthesis code of Cerviño & Mas-Hesse (1994) (hereafter CMHK, see Cerviño et al. 2001a for details),
with the wind treatment illustrated in Cerviño et al. (2001a).
The reasons for considering two different synthesis codes with two different mass-loss laws
reside in the importance of showing the effects of
different assumptions on the wind treatment
(a possibility granted by the Starburst99 code,
which can be set to any of four different laws),
together with the importance of estimating the expected statistical dispersion
in the energy-related quantitities (a possibility granted by the CMHK code,
either analytically or by means of Monte Carlo simulations).
Stated otherwise, it is not our intention to compare the two codes, but rather the two wind treatments:
had we chosen the same one as Cerviño et al. (2001a) in the Starburst99 settings, we would have found the same result as
with the CMHK code.
The two estimates of
![]() obtained with the CMHK code
have been obtained with an analytical and a Monte Carlo representation of the IMF respectively,
and they both take into account the effect of statistical fluctuations in the IMF.
When statistical effects in the IMF are taken into account, the
population properties are no more univocally determined, being instead
distributed along a probability distribution curve.
The characteristic parameters of the curve can be determined analytically
or by means of Monte Carlo simulations (see Cerviño et al. 2001b).
The second line of Table 2 lists the
analytical estimate of the average wind luminosity and the total integrated wind energy
obtained with the CMHK code,
as well as the corresponding 90% confidence intervals
(i.e., the 5th and the 95th percentile).
The third line quotes the same quantitites obtained by means of
Monte Carlo simulations,
again with the uncertainties corresponding to the 90% confidence interval.
These two estimates of
obtained with the CMHK code
have been obtained with an analytical and a Monte Carlo representation of the IMF respectively,
and they both take into account the effect of statistical fluctuations in the IMF.
When statistical effects in the IMF are taken into account, the
population properties are no more univocally determined, being instead
distributed along a probability distribution curve.
The characteristic parameters of the curve can be determined analytically
or by means of Monte Carlo simulations (see Cerviño et al. 2001b).
The second line of Table 2 lists the
analytical estimate of the average wind luminosity and the total integrated wind energy
obtained with the CMHK code,
as well as the corresponding 90% confidence intervals
(i.e., the 5th and the 95th percentile).
The third line quotes the same quantitites obtained by means of
Monte Carlo simulations,
again with the uncertainties corresponding to the 90% confidence interval.
These two estimates of
![]() are in excellent agreement,
showing the consistency of the two statistical approaches of the CMHK code.
In all the cases, the extended burst scenario has been represented as the sum of
individual instantaneous bursts of different ages and roughly equal masses.
In the case of the Monte Carlo method, different simulations, taken
from an ensemble of 5000 runs of 102 stars each, have been summed up
until the mass of each individual cluster was reached.
The total number of independent Monte Carlo simulations
of the extended burst obtained through this procedure was 64.
are in excellent agreement,
showing the consistency of the two statistical approaches of the CMHK code.
In all the cases, the extended burst scenario has been represented as the sum of
individual instantaneous bursts of different ages and roughly equal masses.
In the case of the Monte Carlo method, different simulations, taken
from an ensemble of 5000 runs of 102 stars each, have been summed up
until the mass of each individual cluster was reached.
The total number of independent Monte Carlo simulations
of the extended burst obtained through this procedure was 64.
The average estimates obtained with CMHK give roughly 70% higher luminosity than the Starburst99 value; this is mainly due to the difference between the wind treatment adopted in the two codes, and is not directly related to differences in the spectra, which are, for the scopes of the present work, largely negligible. The integrated energy value obtained with Starburst99 is higher than the CMHK one, a somewhat surprising trend given the corresponding luminosity values. These figures depend on the winds evolution with time: the wind treatment adopted in the Starburst99 calculation gives less energetic winds than the one implemented in the CMHK code at earlier ages, while for ages greater than about 2.5 Myr the relationship is inverted.
| Synthesis code | IMF filling |
|
|
| (1039 erg s-1) | (1052 erg) | ||
| Starburst99 | Analytical | 0.68 | 5.0 |
| CMHK | Analytical | 1.14-0.23+0.27 | 4.34-0.61+0.68 |
| CMHK | Monte Carlo | 1.16-0.20+0.37 | 4.32-0.66+0.88 |
It is now possible to compute the
![]() values
associated with the kinetic energy input,
according to the general expression:
values
associated with the kinetic energy input,
according to the general expression:
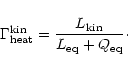 |
(6) |
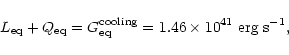 |
(7) |
The
![]() values obtained are listed in
Table 3, together with the inferred
values obtained are listed in
Table 3, together with the inferred
![]() obtained from the hot-spot model of NGC 2363
(cf. Fig. 1);
we will refer to these
obtained from the hot-spot model of NGC 2363
(cf. Fig. 1);
we will refer to these
![]() values with the symbol
values with the symbol
![]() to emphasize that they are inferred under the assumption
that the temperature fluctuations are driven by
the stellar-wind kinetic energy.
All the
to emphasize that they are inferred under the assumption
that the temperature fluctuations are driven by
the stellar-wind kinetic energy.
All the
![]() values obtained are extremely small,
well below the
values obtained are extremely small,
well below the
![]() inferred from observations.
However, there are still a few issues to consider before
drawing any conclusion from the comparison between
the
inferred from observations.
However, there are still a few issues to consider before
drawing any conclusion from the comparison between
the
![]() values of Table 3
and the
values of Table 3
and the
![]() value of NGC 2363 inferred in Sect. 3.1.
value of NGC 2363 inferred in Sect. 3.1.
| Synthesis code | IMF filling |
|
|
| Starburst99 | Analytical | 0.0047 | 0.60 |
| CMHK | Analytical | 0.0076-0.0015+0.0021 | 0.96-0.19+0.30 |
| CMHK | Monte Carlo | 0.0076-0.0011+0.0028 | 0.96-0.14+0.40 |
Copyright ESO 2001