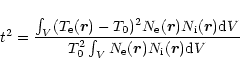 |
(1) |
To quantify the energy injection rate needed to fuel temperature fluctuations in a nebula, we follow the model proposed by Binette & Luridiana (2000) and Binette et al. (2001). The first of these two papers contains a detailed description of the method, while we refer to the second for an alternative representation of the results. The model depicts temperature fluctuations as a collection of hot spots, arising above a uniform equilibrium temperature floor, and fed by an unknown heating agent. This representation allows one to compute the average thermal properties of the nebula in the temperature-fluctuation regime, but without having to compute real localized fluctuations, as described below.
The amplitude of temperature fluctuations in a nebula
is measured by the parameter t2, defined as follows (Peimbert 1967):
On the observational side, González-Delgado et al. (1994) find for knot A in NGC 2363 the value
![]() by comparing the Paschen temperature,
by comparing the Paschen temperature, ![]() (Pa),
to the [ O III] temperature, obtained from the
(Pa),
to the [ O III] temperature, obtained from the
![]() ratio.
Even if in this case the formal error on
ratio.
Even if in this case the formal error on
![]() is quite large
(we calculated
is quite large
(we calculated
![]() ,
mainly due to the large error on
,
mainly due to the large error on ![]() (Pa)),
the differences between the model predictions and the observations
seem to imply that an extra-heating mechanism,
other than photoionization, is at work in most objects,
producing an additional
(Pa)),
the differences between the model predictions and the observations
seem to imply that an extra-heating mechanism,
other than photoionization, is at work in most objects,
producing an additional
![]() such that
such that
![]() .
In the case of NGC 2363, we find
.
In the case of NGC 2363, we find
![]() .
Note that such value still leaves the door open to the possibility, small but not negligible,
that
.
Note that such value still leaves the door open to the possibility, small but not negligible,
that
![]() ;
however, we assume this not to be the case.
In this respect, it is interesting to note that
;
however, we assume this not to be the case.
In this respect, it is interesting to note that
![]() in knot B of the same region (González-Delgado et al. 1994).
Given the presumed age and metallicity of this region (Luridiana et al. 1999),
and assuming the same filling factor as in knot A,
we can roughly estimate
in knot B of the same region (González-Delgado et al. 1994).
Given the presumed age and metallicity of this region (Luridiana et al. 1999),
and assuming the same filling factor as in knot A,
we can roughly estimate
![]() (see, e.g., Pérez 1997),
yielding
(see, e.g., Pérez 1997),
yielding
![]() ,
with an associated error of about
,
with an associated error of about
![]() .
.
More generally, even though the errors might be compatible with
![]() in individual cases of ionized regions with
in individual cases of ionized regions with
![]() ,
this is certainly not the case when large samples are considered.
As an example, galactic H II regions and planetary nebulae collectively show higher
values, typically around 0.04 (e.g., Peimbert et al. 1995; Peimbert 1995, and references
therein).
,
this is certainly not the case when large samples are considered.
As an example, galactic H II regions and planetary nebulae collectively show higher
values, typically around 0.04 (e.g., Peimbert et al. 1995; Peimbert 1995, and references
therein).
The presence of temperature fluctuations inside NGC 2363 bears
important cosmological consequences,
as it affects the determination of the chemical abundances,
lowering the extrapolated primordial helium abundance ![]() (e.g., Peimbert et al. 2001a, and references therein).
In our case,
(e.g., Peimbert et al. 2001a, and references therein).
In our case,
![]() implies a downward change in the helium abundance
of NGC 2363 of order 2%,
the exact figure depending on which He lines the abundance determination is based on
(see also González-Delgado et al. 1994).
It is important to note, however, that temperature fluctuations are not the only factor
affecting a proper chemical abundance determination,
other being, e.g, the ionization structure and the collisional
excitation of the hydrogen lines (Stasinska & Izotov 2001; Peimbert et al. 2001b).
implies a downward change in the helium abundance
of NGC 2363 of order 2%,
the exact figure depending on which He lines the abundance determination is based on
(see also González-Delgado et al. 1994).
It is important to note, however, that temperature fluctuations are not the only factor
affecting a proper chemical abundance determination,
other being, e.g, the ionization structure and the collisional
excitation of the hydrogen lines (Stasinska & Izotov 2001; Peimbert et al. 2001b).
The overall energy balance in a nebula
is described by the following equation:
In the hot-spot model, a particular temperature profile of a hypothetic nebula
is postulated, consisting of a collection of randomly-generated hot spots
arising above the
![]() floor.
Following the definitions of Eqs. (1) and (2),
the
floor.
Following the definitions of Eqs. (1) and (2),
the
![]() and
and ![]() values can be computed,
giving
values can be computed,
giving
![]() and
and
![]() .
The recombination rates of this hypothetic model depend on the assumed
temperature structure, being in general different from those
of the reference
.
The recombination rates of this hypothetic model depend on the assumed
temperature structure, being in general different from those
of the reference
![]() model.
It is possible to account for such variation by introducing
a new "global'' temperature,
model.
It is possible to account for such variation by introducing
a new "global'' temperature,
![]() ,
such that
the intensity of a recombination line is given by:
,
such that
the intensity of a recombination line is given by:
Analogously, the intensity of a collisionally excited line
in the temperature-fluctuation regime can be calculated
by means of a "global'' collisional temperature
![]() ,
such that the collisional excitation and de-excitation rates
are proportional to
,
such that the collisional excitation and de-excitation rates
are proportional to
![]() and
and
![]() respectively, with the
respectively, with the ![]() and
and
![]() values appropriate for each considered line.
values appropriate for each considered line.
Through the definition of these corrected temperatures,
the new line emissivities can be computed in a straightforward way.
In the hot-spot model, the relationship between
![]() and
the derived temperatures is put in analytical form and generalized,
so that the effects of fluctuations on the output quantities
can be easily computed.
For each postulated
and
the derived temperatures is put in analytical form and generalized,
so that the effects of fluctuations on the output quantities
can be easily computed.
For each postulated
![]() value, a plain photoionization model
is calculated, in which the line emissivities are corrected for
the temperature-fluctuation effects,
and the global energy balance is consequently modified.
This energetic change can be expressed
by means of the quantity
value, a plain photoionization model
is calculated, in which the line emissivities are corrected for
the temperature-fluctuation effects,
and the global energy balance is consequently modified.
This energetic change can be expressed
by means of the quantity
![]() ,
defined as follows:
,
defined as follows:
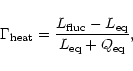 |
(5) |
The relationship between
![]() and
and
![]() depends on the properties of both the ionizing source
and the gaseous nebula.
In Fig. 1 we show the dependence of
depends on the properties of both the ionizing source
and the gaseous nebula.
In Fig. 1 we show the dependence of
![]() on
on
![]() for the Luridiana et al. (1999) model of NGC 2363, which we computed
using a modified version of the photoionization-shock code MAPPINGS IC
(Ferruit et al. 1997).
As a general rule,
a tailored model should be computed for each considered case,
and the calibrations obtained for simpler models
should only be used as rough guidelines when estimating
the energy implications of temperature fluctuations in a given object.
We can illustrate this point comparing our calibration
to the one by Binette & Luridiana (2000) at a representative temperature.
We first introduce an equivalent effective temperature for the cluster,
defined, according to the method by Mas-Hesse & Kunth (1991),
as the temperature of an early-type star with the same
Q(He0)/Q(H0) ratio as the synthetic stellar energy distribution (SED).
Using the calibration by Panagia (1973), we found
an equivalent effective temperature
for the Luridiana et al. (1999) model of NGC 2363, which we computed
using a modified version of the photoionization-shock code MAPPINGS IC
(Ferruit et al. 1997).
As a general rule,
a tailored model should be computed for each considered case,
and the calibrations obtained for simpler models
should only be used as rough guidelines when estimating
the energy implications of temperature fluctuations in a given object.
We can illustrate this point comparing our calibration
to the one by Binette & Luridiana (2000) at a representative temperature.
We first introduce an equivalent effective temperature for the cluster,
defined, according to the method by Mas-Hesse & Kunth (1991),
as the temperature of an early-type star with the same
Q(He0)/Q(H0) ratio as the synthetic stellar energy distribution (SED).
Using the calibration by Panagia (1973), we found
an equivalent effective temperature
![]() .
In Fig. 1 we reproduce
the calibration computed by Binette & Luridiana (2000) for the case
of a constant-density, Z=0.004 nebula ionized by an unblanketed LTE
atmosphere of
.
In Fig. 1 we reproduce
the calibration computed by Binette & Luridiana (2000) for the case
of a constant-density, Z=0.004 nebula ionized by an unblanketed LTE
atmosphere of ![]() K (Hummer & Mihalas 1970).
Although the two curves show the same qualitative behavior,
they rapidly diverge for increasing
K (Hummer & Mihalas 1970).
Although the two curves show the same qualitative behavior,
they rapidly diverge for increasing
![]() values.
values.
![\begin{figure}
\par\includegraphics[width=8.8cm]{H3168f1.ps}\end{figure}](/articles/aa/full/2001/45/aah3168/Timg49.gif) |
Figure 1:
|
Copyright ESO 2001