

Up: Dynamics of the solar
5 Error analysis
For reasons of space we have only displayed results from the May 12
TRACE sequences so far.
The October 14 sequences produce comparable timeslices, Fourier
amplitude maps and Fourier spectra, with as major difference
that the extreme quietness of the solar field makes the C IV construct yet more unreliable and dominated by noise.
Nevertheless, the October 14 sequences provide a different sample
that we use here to judge the reliability of the May 12 results, in
particular the high-frequency parts of the Fourier spectra which
are most sensitive to the nonsimultaneities and the cadence and
timing irregularities of the TRACE image acquisition, which differ
between the two dates.
![\begin{figure}
\par\includegraphics[width=70mm,clip]{jmkf26.eps} %
\par
\end{figure}](/articles/aa/full/2001/45/aah2945/Timg104.gif) |
Figure 26:
Comparison of the spatially averaged
Fourier spectra from May 12 1998
and from October 14 1998.
The solid curves are the same as in
Fig. 18
except that the power spectra are normalised to the
zero-frequency value (square of the mean intensity).
The October 14 spectra are dashed and have a lower Nykvist
frequency (23 mHz).
|
Figure 26 compares Fourier spectra
between the two dates in the format of Fig. 18
(but without scatter clouds and rms curves to avoid overcrowding).
The power spectra are again plotted logarithmically but are now made
comparable by zero-frequency normalisation as in
Eq. (4).
The October 14 power spectra have a higher noise level at high
frequency.
The acoustic peaks are about the same for the two dates.
The phase-difference averages differ much between the two dates from
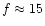 mHz onwards, even in the well-sampled internetwork
(upper panels).
The averaged coherences disagree appreciably at even lower
frequency.
mHz onwards, even in the well-sampled internetwork
(upper panels).
The averaged coherences disagree appreciably at even lower
frequency.
The TRACE fields sample a sizable fraction of the solar disk.
The October 14 field was even quieter than the May 12 field but
there is no reason to assume that the internetwork was
intrinsically different between the two dates in these large
spatial averages.
Thus, we may expect the solar behaviour to have been similar at the
two dates (except for the C IV construct), especially in the
internetwork.
The fact that the mean phase difference and coherence spectra differ
so much above
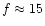 mHz implies that measurement errors
and measurement differences are important and upset our
anticipation of diagnosing high-frequency oscillation properties
exploiting the TRACE virtues of seeing-less and statistically-rich
sampling.
Various tests were therefore made to elucidate these errors.
The principal question is to what frequency the phase-difference
spectra are reliable.
mHz implies that measurement errors
and measurement differences are important and upset our
anticipation of diagnosing high-frequency oscillation properties
exploiting the TRACE virtues of seeing-less and statistically-rich
sampling.
Various tests were therefore made to elucidate these errors.
The principal question is to what frequency the phase-difference
spectra are reliable.
![\begin{figure}
\par\includegraphics[width=80mm,clip]{jmkf27.eps} %
\end{figure}](/articles/aa/full/2001/45/aah2945/Timg106.gif) |
Figure 27:
Phase-difference closure. The curves show
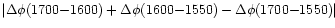 where
each
where
each
 is the vector-averaged mean phase
difference (solid curves
in Figs. 18-19).
Solid: internetwork. Dashed: network.
Upper panel: May 12 data.
Lower panel: October 14 data.
is the vector-averaged mean phase
difference (solid curves
in Figs. 18-19).
Solid: internetwork. Dashed: network.
Upper panel: May 12 data.
Lower panel: October 14 data.
|
![\begin{figure}
\par\includegraphics[width=8cm,clip]{jmkf28.eps} %\end{figure}](/articles/aa/full/2001/45/aah2945/Timg107.gif) |
Figure 28:
Phase-difference tests using 2500 pairs of artificial
solar-like signals with random phase per
frequency in the first signal.
The top panel results when the second signal is identical
to the first one apart from a phase delay of 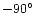 per frequency and both are sampled simultaneously
with the actual TRACE 1600 Å timing sequence.
The solid curve in the middle panel results when the two signals are
identical (without phase delay) but are sampled
TRACE-like with the 1600 and 1700 Å timing sequences,
which have an average offset of 5s. The dotted curve shows
the phase difference for a constant offset of 5s between
signals.
The dotted curve in the bottom panel
shows the combination (two signals
per frequency and both are sampled simultaneously
with the actual TRACE 1600 Å timing sequence.
The solid curve in the middle panel results when the two signals are
identical (without phase delay) but are sampled
TRACE-like with the 1600 and 1700 Å timing sequences,
which have an average offset of 5s. The dotted curve shows
the phase difference for a constant offset of 5s between
signals.
The dotted curve in the bottom panel
shows the combination (two signals 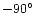 out of phase sampled TRACE-like).
The solid curve includes correction for constant 5s offset
and emulates our phase difference evaluations from the actual data.
The curve in the top panel is overlaid for comparison.
out of phase sampled TRACE-like).
The solid curve includes correction for constant 5s offset
and emulates our phase difference evaluations from the actual data.
The curve in the top panel is overlaid for comparison.
|
A direct reliability test of the phase differences in Figs. 18, 19 is available in the form
of phase-difference closure.
If each passband samples a well-defined oscillation phase per
frequency, the
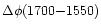 differences should
equal the summed
differences should
equal the summed
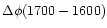 and
and
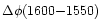 values.
Figure 27 shows that the direct and summed
evaluations depart between f=10 and f=15 mHz, and for the
network at somehat lower frequencies.
This is the same frequency region in which the phase-difference
spectra in Fig. 26 depart from each
other, indicating that the averaged phase-difference spectra in
Figs. 18, 19 indeed become
unreliable in this frequency band.
values.
Figure 27 shows that the direct and summed
evaluations depart between f=10 and f=15 mHz, and for the
network at somehat lower frequencies.
This is the same frequency region in which the phase-difference
spectra in Fig. 26 depart from each
other, indicating that the averaged phase-difference spectra in
Figs. 18, 19 indeed become
unreliable in this frequency band.
In standard practice, the 10% start and end segments of the
brightness sequence per pixel were multiplied by a
10% cosine bell taper to the mean value in order to suppress window edge
effects.
The original mean was restored as zero-frequency amplitude after the
transform.
Tests changing or even deleting the edge taper produced more
high-frequency noise as expected from edge discontinuities
(Brault & White 1971), but no significant change in
phase-difference behaviour.
TRACE has no high-frequency filter to suppress noise above the Nykvist
frequency.
The power curves in Fig. 18 still decrease slightly
close to the Nykvist frequency, so that some aliasing seems indeed
to occur.
However, the Nykvist frequency is quite high in the May 12 data.
The power spectra are appreciably higher around f=15 mHz so that
the phase-difference spectra should be dominated by non-aliased
signal around this frequency.
However, at higher frequencies the sampling itself becomes
inadequate for phase measurements below the Nykvist frequency.
These imply a three-parameter sinusoidal fit (amplitude, offset, and
phase) to each signal per frequency and pixel, so that the
uncertainties increase rapidly when the signal is sampled less then
3 times per period, i.e. above
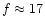 mHz for the May 12
data.
mHz for the May 12
data.
The worst phase-difference error source is the non-simultaneity of the
imaging in the different passbands.
In principle, the temporal offset between the samples in two
sequences introduces phase difference at each frequency that equals
the offset divided by the period, a linear increase with frequency
that was corrected using the equidistant time scale defined for
each dataset.
(The correction also makes
 depart from
depart from 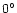 or
or
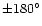 at the Nykvist frequency.) However, the actual timing
irregularities and exposure durations cause uncertainties that also
increase with frequency and become quite large at the
high-frequency end - as demonstrated below.
at the Nykvist frequency.) However, the actual timing
irregularities and exposure durations cause uncertainties that also
increase with frequency and become quite large at the
high-frequency end - as demonstrated below.
Figure 28 illustrates the effects of the major
sampling errors on phase-difference measurements by using an
artificially generated signal that possesses a solar-like power
spectrum.
Statistical variation was introduced by generating 2500 realizations
in each of which the phase was chosen randomly at each frequency.
The top panel illustrates errors due to discrete sampling and
sampling irregularities alone.
It uses the actual mid-exposure timing sequence of the May 12
1600Å data to measure phase differences between the 2500
artificial signals and 2500 copies that are phase-shifted over
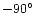 at each frequency.
The curve shows the result from vector-averaged phase-difference
determination as done above.
The deviations from
at each frequency.
The curve shows the result from vector-averaged phase-difference
determination as done above.
The deviations from
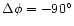 illustrate the errors
caused by the non-equidistant exposure timing.
They are reasonably small out to high frequencies.
illustrate the errors
caused by the non-equidistant exposure timing.
They are reasonably small out to high frequencies.
The middle panel of Fig. 28 shows a similar test
using 2500 pairs of identical (not phase-shifted) signals sampled
with the actual 1600 and 1700 Å timing sequences.
The noise increases considerably compared with the top panel.
The bottom panel results from a 2500-pair test combining the two error
sources.
It indicates that the irregular sampling of different signals at
unequal times introduces large errors that cause appreciable
 distortion for frequencies above f=10 mHz and large
distortion for frequencies above f=10 mHz and large
 scatter above f=20 mHz.
The phase closure test in Fig. 27 indicates a
somewhat larger extent of reliability, out to f=15 mHz for errors
below
scatter above f=20 mHz.
The phase closure test in Fig. 27 indicates a
somewhat larger extent of reliability, out to f=15 mHz for errors
below 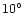 ,
in the internetwork which provided more samples than
the 2500 used in these tests.
The internetwork
,
in the internetwork which provided more samples than
the 2500 used in these tests.
The internetwork
 curves in
Fig. 26 also show equality up to
f=15 mHz.
curves in
Fig. 26 also show equality up to
f=15 mHz.
The conclusion is that, even though the TRACE data do not suffer from
seeing, the sequential nature of TRACE's filter-wheel switching
between passbands combined with the sampling irregularity
is the major contributor of phase-difference noise and limits the
reliability of the
 spectra in Figs. 18, 19 to frequencies below
spectra in Figs. 18, 19 to frequencies below
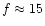 mHz.
mHz.


Up: Dynamics of the solar
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=70mm,clip]{jmkf26.eps} %
\par
\end{figure}](/articles/aa/full/2001/45/aah2945/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=80mm,clip]{jmkf27.eps} %
\end{figure}](/articles/aa/full/2001/45/aah2945/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{jmkf28.eps} %\end{figure}](/articles/aa/full/2001/45/aah2945/Timg107.gif)