

Up: Dynamics of the solar
3 Fourier analysis
We briefly review our evaluations of Fourier quantities from the TRACE
data.
The analysis is standard following Edmonds & Webb (1972),
Paper I, and
Lites et al. (1998), but there are various display choices
that require discussion.
We write the temporal Fourier transform
of a time sequence
f1 (x,y,t)
for solar location (x,y) as
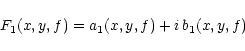 |
(1) |
where a1 and b1 are real numbers, t represents time and ftemporal frequency. The subscript 1 indicates a particular
TRACE sequence.
The cross-correlation spectrum between two simultaneous
sequences 1 and 2 per location (x,y) is
| F12(x,y,f) |
= |
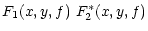 |
|
| |
= |
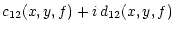 |
(2) |
where the asterisk indicates the complex conjugate and
c12 and d12 are real numbers.
Standard choices for the display of power spectra are
to plot the modulation energy
|
PE(x,y,f) = a(x,y,f)2+b(x,y,f)2,
|
(3) |
the fractional modulation
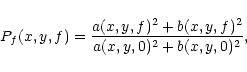 |
(4) |
or to use Leahy normalisation
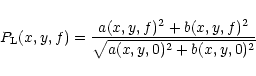 |
(5) |
(Leahy et al. Leahy et al. 1983,
cf. van der Klis 1989,
Appendix of
Doyle et al. 1999). The latter serves to estimate the significance of periodic signals but
is not used here.
This choice in normalisation does not affect the relative shape of an
individual power spectrum but becomes important when comparing or
averaging different signals.
For example, if some wave process dissipates the same amount of
energy at the wave frequency both in network and internetwork
locations, using (3) without normalisation is
appropriate.
Fractional power normalisation (4) would
underestimate the network dissipation in that case because network
is consistently brighter, but it becomes the right measure when
both network and internetwork are affected by the same
multiplicative modulation process.
We illustrate such differences below.
The phase-difference spectrum is
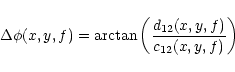 |
(6) |
where positive values of
 imply that
signal 1 is retarded with respect to signal 2.
Different strategies exist to display and average phase differences
imply that
signal 1 is retarded with respect to signal 2.
Different strategies exist to display and average phase differences
 .
The simplest one is to simply display all samples per
temporal frequency in an unweighted scatter diagram
(e.g., Gouttebroze et al. 1999), neglecting the amplitudes of the contributing Fourier components,
or to display the scatter point density as brightness
(e.g., Kneer & von Uexküll 1993). Another extreme is to display only spatial averages per frequency
through averaging
over a spatial wavenumber kh segment or an annulus in the (kx,ky)spatial transform plane
(e.g., Deubner et al. 1992).
We prefer, as in older work, to visualise also the scatter itself in order
to permit appreciation of its distribution.
Lites & Chipman (1979) applied weighting per (x,y,f) sample by the cross-power amplitude
.
The simplest one is to simply display all samples per
temporal frequency in an unweighted scatter diagram
(e.g., Gouttebroze et al. 1999), neglecting the amplitudes of the contributing Fourier components,
or to display the scatter point density as brightness
(e.g., Kneer & von Uexküll 1993). Another extreme is to display only spatial averages per frequency
through averaging
over a spatial wavenumber kh segment or an annulus in the (kx,ky)spatial transform plane
(e.g., Deubner et al. 1992).
We prefer, as in older work, to visualise also the scatter itself in order
to permit appreciation of its distribution.
Lites & Chipman (1979) applied weighting per (x,y,f) sample by the cross-power amplitude
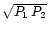 (with
P1 = a12+b12 and
P2 = a22+b22)
to produce binned greyscale
(with
P1 = a12+b12 and
P2 = a22+b22)
to produce binned greyscale
 displays with normalisation
per temporal frequency bin.
In Paper I
only the samples with the highest mean Fourier amplitude
displays with normalisation
per temporal frequency bin.
In Paper I
only the samples with the highest mean Fourier amplitude
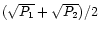 were plotted as scatter diagrams.
were plotted as scatter diagrams.
In this paper we show binned greyscale scatter plots with
cross-power amplitude sample weighting following
Lites & Chipman (1979).
We overlay spatially-averaged phase difference curves following
Lites et al. (1998), given per sampled frequency by
![$\displaystyle [\Delta\phi]_{xy}(f)$](/articles/aa/full/2001/45/aah2945/img44.gif) |
= |
![$\displaystyle \arctan
\left(
\frac{[d_{12}(x,y,f)]_{xy}}{ [c_{12}(x,y,f)]_{xy}}
\right)$](/articles/aa/full/2001/45/aah2945/img45.gif) |
(7) |
where the square brackets express averaging over locations (x,y).
This procedure equals vector addition of the individual
cross-correlation samples with each vector length set by the
product of the two Fourier amplitudes so that the cross-power
amplitudes again act as weights in setting the slope of the summed
vector.
The procedure avoids wraparound errors that occur in straightforward
averaging from the 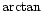 evaluation, for example when a value
just above
evaluation, for example when a value
just above 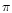 is transformed into one just above
is transformed into one just above 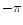 and then
averages erroneously with one just below
and then
averages erroneously with one just below 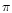 to
to
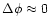 instead of
instead of
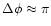 .
.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{jmkf5.eps}
\end{figure}](/articles/aa/full/2001/45/aah2945/Timg51.gif) |
Figure 5:
Partial cutouts from the May 12 1700Å
sequence illustrating
temporal variations at 30s cadence.
The numbers specify elapsed time from 15:26:32 UT in seconds.
Axes: X and Y in arcsec from disk center.
The greyscale is logarithmic.
The first panel is a central cutout of the top panel in
Fig. 2.
The white markers along the sides of this panel specify the
horizontal cut location used in
Figs. 6-7. The white
box marks the yet smaller subfield which is duplicated in the
third column using a sign-reversed logarithmic greyscale to
display the slowly-varying internetwork background pattern.
Taking the inverse emphasizes the internetwork features by
darkening the network and makes the brightness minima of the
three-minute oscillation appear as brightest features. These
reversed extrema appear to travel fast along the strands of a
more persistent background mesh which we attribute to
gravity-wave interference. Similar behaviour is seen, in
counterphase, for the bright internetwork grains on non-inverted but
rapidly displayed movies such as the ones on
URL
http://www.astro.uu.nl/~rutten/trace1 from which this
figure is derived. The grain-to-mesh superposition is also
visualized in Fig. 11.
|
There is also a choice for the
evaluation of the degree of coherence between two
signals.
It requires some sort of local temporal or spatial averaging,
because without any smoothing the coherence between two sinusoidal
Fourier components at given (x,y,f) is unity regardless of the
corresponding Fourier amplitudes and phase difference.
The Würzburg practice of annular kh averaging has the advantage
that adjacent frequencies are treated independently, but the
disadvantage that the modulations are assumed isotropic.
Note that in this case the mean coherence goes to zero for pure
noise.
In contrast, Lites and coworkers treat each spatial pixel as
an independent sample of solar behaviour but average over a frequency
interval
(Paper I![[*]](/icons/foot_motif.gif) ,
Lites et al. 1998),
a tactic necessarily followed also in the one-dimensional phase
modelling of
Skartlien et al. (1994).
For pure noise this procedure yields positive coherence
,
Lites et al. 1998),
a tactic necessarily followed also in the one-dimensional phase
modelling of
Skartlien et al. (1994).
For pure noise this procedure yields positive coherence
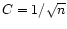 when averaging a sufficiently large
sample, with n the number of frequency resolution elements
per averaging interval.
We use the latter method, selecting boxcar frequency
smoothing that is represented by
angle brackets in writing the coherence as
when averaging a sufficiently large
sample, with n the number of frequency resolution elements
per averaging interval.
We use the latter method, selecting boxcar frequency
smoothing that is represented by
angle brackets in writing the coherence as
The spatially averaged coherence per frequency is then:
![\begin{displaymath}[C^2]_{xy}(f)
= \frac{[<c_{12}>^2]_{xy}+[<d_{12}>^2]_{xy}}
{[<a_1^2+b_1^2>\,<a_2^2+b_2^2>]_{xy}}\cdot
\end{displaymath}](/articles/aa/full/2001/45/aah2945/img56.gif) |
(10) |
We determined and Fourier-transformed the temporal brightness
variation per pixel using equidistant time sampling with
closest-neighbour image selection as discussed above, 10% cosine bell windowing, and replacing the zero-frequency
transform values by the original mean brightness.
We applied frequency smoothing for the coherence evaluations with
n=5 so that pure noise has C = 0.45.
The phase differences between different TRACE passbands were
corrected for the temporal shifts between their respective sampling
scales.
The shifts result from the sequential TRACE image taking and produce
artificial phase shifts that increase linearly with frequency when
measured as phase-difference angle.
Other effects from the sequential sampling are discussed in
Sect. 6.
The resulting Fourier power spectra, phase-difference spectra and
coherence spectra per solar location were spatially averaged over
the network and internetwork pixel categories, respectively.
We do not show results for the intermediate pixel category when
these are indeed intermediate between network and internetwork.


Up: Dynamics of the solar
Copyright ESO 2001
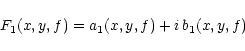
![\begin{figure}
\par\includegraphics[width=12cm,clip]{jmkf5.eps}
\end{figure}](/articles/aa/full/2001/45/aah2945/Timg51.gif)