

Up: Pick-up ions upstream and
We now want to derive the postshock PUI spectrum starting from the
upstream spectrum at the shock given in Eq. (12). In the following we
shall give expressions for spectra of those PUIs which upon arrival at
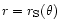 directly pass over the local shock transition and
consequently exclude those which undergo a reflection at the electric
potential ramp of the shock and move upstream again (as described e.g.
by
Kucharek & Scholer 1995; Chalov & Fahr
1996,2000; Lee et al. 1996; Zank et al.
1996; Giacalone & Jokipii 1998;
Scholer & Kucharek 1999; Le Roux et al. 2000). The relative abundance of these
reflected ions as calculated by Chalov & Fahr
(1996) is, however, of the order of 10 percent or less.
directly pass over the local shock transition and
consequently exclude those which undergo a reflection at the electric
potential ramp of the shock and move upstream again (as described e.g.
by
Kucharek & Scholer 1995; Chalov & Fahr
1996,2000; Lee et al. 1996; Zank et al.
1996; Giacalone & Jokipii 1998;
Scholer & Kucharek 1999; Le Roux et al. 2000). The relative abundance of these
reflected ions as calculated by Chalov & Fahr
(1996) is, however, of the order of 10 percent or less.
Here we use index "1'' for upstream quantities and index "2'' for
corresponding downstream quantities. We assume that the distribution
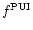 is isotropic in velocity (i.e. due to strong pitch-angle
diffusion by quasilinear wave-particle interaction). We also assume that
the magnetic moment of the PUI is conserved when crossing the shock, which
requires that the shock transition should be wide as compared to the PUI
Larmor radius. At the PUI passage over the shock the
following changes in the PUI distribution function have to be considered
(we follow Fahr & Lay 2000):
is isotropic in velocity (i.e. due to strong pitch-angle
diffusion by quasilinear wave-particle interaction). We also assume that
the magnetic moment of the PUI is conserved when crossing the shock, which
requires that the shock transition should be wide as compared to the PUI
Larmor radius. At the PUI passage over the shock the
following changes in the PUI distribution function have to be considered
(we follow Fahr & Lay 2000):
1) total densities are increased by the compression ratio:
![\begin{displaymath}s(\theta)=[\rho_2/\rho_1]_{\theta}=[U_{1\perp}/U_{2\perp}]_{\theta}
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img82.gif) |
(13) |
where
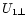 and
and
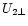 are the upstream and downstream
solar wind bulk velocity components perpendicular to the local shock surface.
are the upstream and downstream
solar wind bulk velocity components perpendicular to the local shock surface.
2) due to the local downstream increase in the magnetic field magnitude
by the local factor
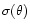 in connection with a conserved
magnetic moment of PUIs passing over the shock there is a change in the
particle energy characterized by:
in connection with a conserved
magnetic moment of PUIs passing over the shock there is a change in the
particle energy characterized by:
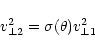 |
(14) |
where
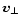 is the particle velocity perpendicular to the
magnetic field. For an isotropic distribution
is the particle velocity perpendicular to the
magnetic field. For an isotropic distribution
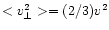 .
This gives the result
.
This gives the result
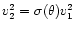 ,
,
and:
3) due to the differential flux conservation over the shock (Liouville
theorem) one obtains:
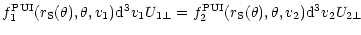 |
|
(15) |
which leads to:
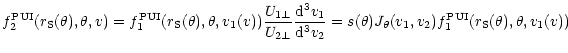 |
|
|
(16) |
where
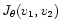 is the Jacobian of the transformation of
preshock to postshock velocities given by:
is the Jacobian of the transformation of
preshock to postshock velocities given by:
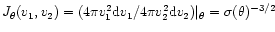 and where again
and where again
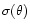 is the field
compression ratio at
is the field
compression ratio at
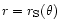 which is extracted from the result
of the 5-fluid counterflow simulation model published by Fahr et al.
(2000) as we shall show below.
which is extracted from the result
of the 5-fluid counterflow simulation model published by Fahr et al.
(2000) as we shall show below.
The derivation of
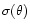 is carried out by the following
argumentation: at the position
is carried out by the following
argumentation: at the position
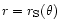 the upstream magnetic
field can be split into components parallel and perpendicular to the
shock surface, yielding:
the upstream magnetic
field can be split into components parallel and perpendicular to the
shock surface, yielding:
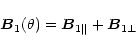 |
(17) |
with
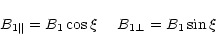 |
(18) |
with 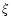 being the angle between the upstream field
being the angle between the upstream field 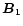 and
the shock surface (or between the upstream solar wind velocity
and
the shock surface (or between the upstream solar wind velocity
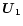 and the shock normal
and the shock normal
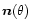 ). In the ecliptic
the angle
). In the ecliptic
the angle 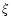 is connected with the local curvature of the shock
surface and is given by:
is connected with the local curvature of the shock
surface and is given by:
![\begin{displaymath}{\rm tg} \xi=r_{\rm S}(\theta)/[\partial r_{\rm S}/\partial\theta]_{\theta}=
r_{\rm S}/r_{S,\theta}
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img100.gif) |
(19) |
and is obtained from the form of
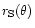 given by Fahr et al.
(2000). The downstream magnetic field now is given by:
given by Fahr et al.
(2000). The downstream magnetic field now is given by:
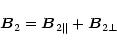 |
(20) |
with
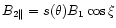 and
and
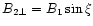 .
.
The magnitude of the downstream magnetic field thus is given by:
![\begin{displaymath}B_2(\theta)=s(\theta)B_1(\theta)[\cos^2 \xi+\sin^2 \xi/s^2(\theta)]^{1/2}.
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img104.gif) |
(21) |
Replacing now 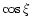 and
and 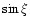 by
by
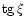 given in Eq.
(19) yields:
given in Eq.
(19) yields:
![\begin{displaymath}\sigma(\theta)=s(\theta)(1+{\rm tg}^2\xi)^{-1/2}
[1+{\rm tg}^2\xi/s^2(\theta)]^{1/2}.
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img108.gif) |
(22) |
Taking all these results together leads to:
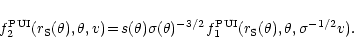 |
(23) |
This on basis of Eq. (12) delivers the following postshock PUI spectrum:
![$\displaystyle f^{\rm PUI}_2(r_{\rm S}(\theta),\theta,v)
=\nu(\theta)s(\theta)\s...
...e}^{-[C_K(X_{\rm S}(\theta))\sigma(\theta)^{-K}(w-w_0)^K]}}
{2\pi U_0 \sqrt{w}}$](/articles/aa/full/2001/44/aah2973/img110.gif) |
|
|
(24) |
with
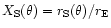 and
w=(v/U0)2.
and
w=(v/U0)2.
The resulting PUI fluxes immediately downstream of the shock are
presented in Fig. 3 for three different positions at the shock
surface. These are compared
with extrapolated anomalous cosmic ray proton spectrum at the shock
deduced from de-modulation of the observed high-energy ACR spectrum (Stone
et al. 1996).


Up: Pick-up ions upstream and
Copyright ESO 2001
![]() directly pass over the local shock transition and
consequently exclude those which undergo a reflection at the electric
potential ramp of the shock and move upstream again (as described e.g.
by
Kucharek & Scholer 1995; Chalov & Fahr
1996,2000; Lee et al. 1996; Zank et al.
1996; Giacalone & Jokipii 1998;
Scholer & Kucharek 1999; Le Roux et al. 2000). The relative abundance of these
reflected ions as calculated by Chalov & Fahr
(1996) is, however, of the order of 10 percent or less.
directly pass over the local shock transition and
consequently exclude those which undergo a reflection at the electric
potential ramp of the shock and move upstream again (as described e.g.
by
Kucharek & Scholer 1995; Chalov & Fahr
1996,2000; Lee et al. 1996; Zank et al.
1996; Giacalone & Jokipii 1998;
Scholer & Kucharek 1999; Le Roux et al. 2000). The relative abundance of these
reflected ions as calculated by Chalov & Fahr
(1996) is, however, of the order of 10 percent or less.
![]() is isotropic in velocity (i.e. due to strong pitch-angle
diffusion by quasilinear wave-particle interaction). We also assume that
the magnetic moment of the PUI is conserved when crossing the shock, which
requires that the shock transition should be wide as compared to the PUI
Larmor radius. At the PUI passage over the shock the
following changes in the PUI distribution function have to be considered
(we follow Fahr & Lay 2000):
is isotropic in velocity (i.e. due to strong pitch-angle
diffusion by quasilinear wave-particle interaction). We also assume that
the magnetic moment of the PUI is conserved when crossing the shock, which
requires that the shock transition should be wide as compared to the PUI
Larmor radius. At the PUI passage over the shock the
following changes in the PUI distribution function have to be considered
(we follow Fahr & Lay 2000):
![\begin{displaymath}s(\theta)=[\rho_2/\rho_1]_{\theta}=[U_{1\perp}/U_{2\perp}]_{\theta}
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img82.gif)
![]() in connection with a conserved
magnetic moment of PUIs passing over the shock there is a change in the
particle energy characterized by:
in connection with a conserved
magnetic moment of PUIs passing over the shock there is a change in the
particle energy characterized by:
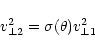
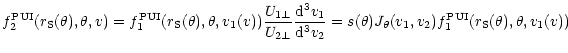
![]() is carried out by the following
argumentation: at the position
is carried out by the following
argumentation: at the position
![]() the upstream magnetic
field can be split into components parallel and perpendicular to the
shock surface, yielding:
the upstream magnetic
field can be split into components parallel and perpendicular to the
shock surface, yielding:
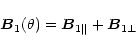
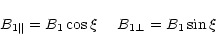
![\begin{displaymath}{\rm tg} \xi=r_{\rm S}(\theta)/[\partial r_{\rm S}/\partial\theta]_{\theta}=
r_{\rm S}/r_{S,\theta}
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img100.gif)
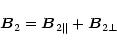
![\begin{displaymath}B_2(\theta)=s(\theta)B_1(\theta)[\cos^2 \xi+\sin^2 \xi/s^2(\theta)]^{1/2}.
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img104.gif)
![\begin{displaymath}\sigma(\theta)=s(\theta)(1+{\rm tg}^2\xi)^{-1/2}
[1+{\rm tg}^2\xi/s^2(\theta)]^{1/2}.
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img108.gif)
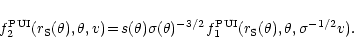
![$\displaystyle f^{\rm PUI}_2(r_{\rm S}(\theta),\theta,v)
=\nu(\theta)s(\theta)\s...
...e}^{-[C_K(X_{\rm S}(\theta))\sigma(\theta)^{-K}(w-w_0)^K]}}
{2\pi U_0 \sqrt{w}}$](/articles/aa/full/2001/44/aah2973/img110.gif)