In the region downstream from the termination shock the plasma flow is
slower (![]() 100 kms-1) and the temperature higher (
100 kms-1) and the temperature higher (![]() 150-300 eV)
than in the region upstream. The protons picked up by the flow will
then be mixed with the thermal population.
150-300 eV)
than in the region upstream. The protons picked up by the flow will
then be mixed with the thermal population.
To estimate the post-shock spatial and energetic distributions of the pick-up ions originating in the upstream region we apply the method used previously in the study of the low-energy ACR distribution (see Czechowski et al. 1995,1999c,2001; an application to PUI was presented in Czechowski et al. 1999a). The pitch-angle-averaged distribution function is obtained as a solution of Parker's transport equation. The PUI distribution function immediately after the shock obtained in the previous section is used as a boundary condition for the numerical solution downstream.
The solution downstream will thus be shaped by the
effects of convection by the plasma flow (described by the velocity field
![]() ), losses predominantly due to charge-exchange with the neutral
background atoms (loss rate
), losses predominantly due to charge-exchange with the neutral
background atoms (loss rate ![]() ), spatial diffusion described by
the
diffusion tensor
), spatial diffusion described by
the
diffusion tensor ![]() and adiabatic energy change due to nonzero
divergence of plasma flow
and adiabatic energy change due to nonzero
divergence of plasma flow
![]() .
The plasma flow and its
divergence (and also the background neutral density needed to
determine
.
The plasma flow and its
divergence (and also the background neutral density needed to
determine ![]() )
are taken from Kausch's model (Kausch 1998; Fahr et al.
2000). The charge-exchange cross sections are taken from
Barnett et al. (1990). We make the scalar diffusion
approximation, which in the region between the termination shock and the
heliopause may be adequate in lowest order. The diffusion
coefficient is assumed to change at the heliopause. Inside the heliopause
we assume
)
are taken from Kausch's model (Kausch 1998; Fahr et al.
2000). The charge-exchange cross sections are taken from
Barnett et al. (1990). We make the scalar diffusion
approximation, which in the region between the termination shock and the
heliopause may be adequate in lowest order. The diffusion
coefficient is assumed to change at the heliopause. Inside the heliopause
we assume
![]() with
with
![]() the parallel diffusion coefficient derived from the
modulation models (we take the formula of Le Roux et al. 1996) while outside the heliopause the diffusion coefficient is
taken to be much larger than inside:
the parallel diffusion coefficient derived from the
modulation models (we take the formula of Le Roux et al. 1996) while outside the heliopause the diffusion coefficient is
taken to be much larger than inside:
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2973f4.eps} %
\end{figure}](/articles/aa/full/2001/44/aah2973/Timg118.gif) |
Figure 4:
PUI density distribution for 2.5 keV protons outside the
termination shock. The density profiles are shown for
|
Parker's equation for the pitch angle averaged distribution function f
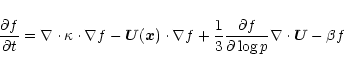 |
(25) |
We assume the solution to be axially symmetric with respect to the LISM
flow apex-antiapex line. As the arguments leading to the post-shock form
of the distribution are applicable only in the ecliptic, we must
interpret the result as applicable also only near to the ecliptic plane.
The boundary conditions used in our approach are defined as follows. At
the termination shock surface we set the distribution function
![]() to
be equal to the post-shock form of the upstream solution. At large
distance the solution is required to match the asymptotic form
(corresponding to constant plasma speed
to
be equal to the post-shock form of the upstream solution. At large
distance the solution is required to match the asymptotic form
(corresponding to constant plasma speed
![]() ).
At the boundaries
in energy space we prescribe the slope of the energy spectrum, which we
set to the value of the slope of the downstream shock spectrum.
).
At the boundaries
in energy space we prescribe the slope of the energy spectrum, which we
set to the value of the slope of the downstream shock spectrum.
The choice of the boundary conditions in energy, which must be done at each point in space, is (except for the requirement of consistency with the energy spectrum assumed at the shock) an arbitrary procedure, unless the behaviour of the ion distribution at the limits in energy is known (Czechowski et al. 1999c,2001). To estimate the resulting uncertainty we have checked different cases, varying the energy limits and assuming different slopes. We found that the choice of the boundary conditions in energy affects the solution in the region close to the energy limits, but the effect in the remaining region is small.
The calculations were done for two cases, corresponding to two cases of
the upstream solution: ![]() and
and ![]() (the latter case is
the extreme one used only for comparison, see Sect. 1).
Because the proton flux behaves differently for these cases, we set the
upper energy limit to 100 keV for the first case and to
1000 keV for the second. The low energy limit we set to 1 keV (see above).
(the latter case is
the extreme one used only for comparison, see Sect. 1).
Because the proton flux behaves differently for these cases, we set the
upper energy limit to 100 keV for the first case and to
1000 keV for the second. The low energy limit we set to 1 keV (see above).
The spatial pick-up protons distributions downstream from the shock
for two values of energy are presented in Figs. 4 and 5 in the form of
constant direction profiles. The angle ![]() is counted from the LISM
apex direction. The density profiles start at the termination shock (which
has the radius dependent on
is counted from the LISM
apex direction. The density profiles start at the termination shock (which
has the radius dependent on ![]() i.e. is non-spherical) and show a
sharp change in slope at the heliopause. In Fig. 4 one can
see a trough in the low energy (2.5 keV) proton density near
i.e. is non-spherical) and show a
sharp change in slope at the heliopause. In Fig. 4 one can
see a trough in the low energy (2.5 keV) proton density near
![]() ,
which is responsible for the dip in the low energy
(<3 keV) ENA flux from the antiapex direction (see Fig. 9). Figure 5 presents the typical distribution in the high PUI energy range (100
keV). Because the PUI energy spectrum is steep at high energy the effect
of the adiabatic acceleration in the heliotail (in the region where
,
which is responsible for the dip in the low energy
(<3 keV) ENA flux from the antiapex direction (see Fig. 9). Figure 5 presents the typical distribution in the high PUI energy range (100
keV). Because the PUI energy spectrum is steep at high energy the effect
of the adiabatic acceleration in the heliotail (in the region where
![]() :
Czechowski et al. 2001) is
quite
pronounced (a "bump'' in the
:
Czechowski et al. 2001) is
quite
pronounced (a "bump'' in the
![]() and
and ![]() profiles in
Fig. 5).
profiles in
Fig. 5).
The energy spectra are presented in Figs. 6 and 7 for different heliocentric distances. The higher depletion of low energy particles with the distance is caused by charge-exchange processes (Czechowski et al. 1999c).
Copyright ESO 2001