

Up: Pick-up ions upstream and
Soon after their injection into the magnetized solar wind
plasma flow, the pick-up ions isotropize their initial ring distribution
due to effective pitch-angle scattering processes. The resulting pitch-angle
isotropized distribution function,
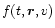 ,
is found as a
solution of the following kinetic transport equation (see e.g. Lee
1983; Isenberg 1987; Bogdan et al.
1991):
,
is found as a
solution of the following kinetic transport equation (see e.g. Lee
1983; Isenberg 1987; Bogdan et al.
1991):
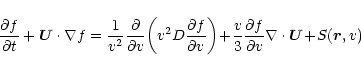 |
(1) |
where
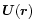 is the solar wind velocity, v is the
velocity of pick-up ions in the solar wind rest frame,
is the solar wind velocity, v is the
velocity of pick-up ions in the solar wind rest frame,
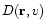 is the energy diffusion coefficient for pick-up ions, and
is the energy diffusion coefficient for pick-up ions, and
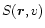 is the local production rate of freshly ionized
particles.
is the local production rate of freshly ionized
particles.
In the following we shall assume axial symmetry with the symmetry axis
parallel to the LISM wind vector
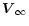 .
This in effect
restricts our considerations to the vicinity
of the ecliptic plane. Using spherical polar coordinates
.
This in effect
restricts our considerations to the vicinity
of the ecliptic plane. Using spherical polar coordinates
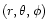 ,
with the Sun as the origin and the polar axis oriented to the interstellar
upwind direction (i.e.
,
with the Sun as the origin and the polar axis oriented to the interstellar
upwind direction (i.e.
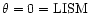 upwind direction), the above
transport equation (Eq. (1)) after introduction of the differential phase
space density,
upwind direction), the above
transport equation (Eq. (1)) after introduction of the differential phase
space density,
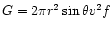 attains the following form (see Chalov et al. 1997):
attains the following form (see Chalov et al. 1997):
where
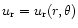 and
and
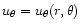 are the
radial and tangential
components of the mass-loaded solar wind velocity. Equation (2) then is solved
numerically by further converting this nonlinear partial differential
equation of second order into an equivalent system of linear stochastic
differential equations (SDE-system). Further details can be found in
papers by Chalov et al. (1995,1997) or by Fahr
& Lay (2000).
are the
radial and tangential
components of the mass-loaded solar wind velocity. Equation (2) then is solved
numerically by further converting this nonlinear partial differential
equation of second order into an equivalent system of linear stochastic
differential equations (SDE-system). Further details can be found in
papers by Chalov et al. (1995,1997) or by Fahr
& Lay (2000).
The injection source
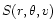 is due to neutral H atoms which
become ionized at
is due to neutral H atoms which
become ionized at
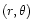 .
These neutral
LISM H atoms penetrate from interstellar space into the interface
region of perturbed solar wind and interstellar plasma flows and with
some depletion eventually appear in the inner heliosphere being subject
to ionization processes there. When these neutral atoms are ionized,
they constitute the H+-pick-up ion production rate
.
These neutral
LISM H atoms penetrate from interstellar space into the interface
region of perturbed solar wind and interstellar plasma flows and with
some depletion eventually appear in the inner heliosphere being subject
to ionization processes there. When these neutral atoms are ionized,
they constitute the H+-pick-up ion production rate
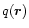 .
The local heliospheric pick-up H+-production rate is
given by the following formula (see Rucinski et al. 1993):
.
The local heliospheric pick-up H+-production rate is
given by the following formula (see Rucinski et al. 1993):
![\begin{displaymath}q(\vec{r})=n_{\rm H}(\vec{r})[\nu_{\rm ph}(\vec{r})+\nu_{\rm ex}(\vec{r})]
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img33.gif) |
(3) |
where
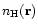 is the number density of the neutral H-atoms
in the heliosphere, and
is the number density of the neutral H-atoms
in the heliosphere, and
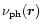 and
and
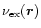 are the relevant local photoionization and charge exchange frequencies.
In Chalov et al. (1995,1997) the densities
are the relevant local photoionization and charge exchange frequencies.
In Chalov et al. (1995,1997) the densities
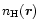 are
calculated within the self-consistent twin-shock interface model
developed by Baranov & Malama (1993) with LISM parameters
fixed in accordance with settings made by these authors. The total pick-up
ion production rate given in Eq. (3) is related to the injection source
are
calculated within the self-consistent twin-shock interface model
developed by Baranov & Malama (1993) with LISM parameters
fixed in accordance with settings made by these authors. The total pick-up
ion production rate given in Eq. (3) is related to the injection source
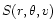 in Eq. (2) by
in Eq. (2) by
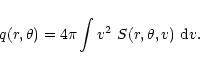 |
(4) |
We assume that
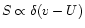 ,
where U is the local solar wind
speed. Our assumption of a narrow initial pick-up ion distribution is a
simplification (see Zank & Cairns 2000). The interplanetary
magnetic field in reality will deviate from the Archimedean spiral as
given by the Parker model and used here. The primary injection thus occurs
into a plasma flow which has a varying magnetic field orientation, leading
to different parallel component of the pick-up ions velocity. The freshly
injected PUIs will be slipping with respect to the bulk flow and tend
to accumulate in the regions where B is
perpendicular to the flow. This situation may be represented by an
injection with a broadened delta peak.
Also, as discussed by Zank & Cairns (2000), the
wave excitation during the pick-up in quasi-perpendicular magnetic field
is less efficient than expected. However, the effect on our results would
be probably restricted to the low energy part of the spectrum, and the
results for the energies significantly higher than the initial spectrum
width would not be changed.
,
where U is the local solar wind
speed. Our assumption of a narrow initial pick-up ion distribution is a
simplification (see Zank & Cairns 2000). The interplanetary
magnetic field in reality will deviate from the Archimedean spiral as
given by the Parker model and used here. The primary injection thus occurs
into a plasma flow which has a varying magnetic field orientation, leading
to different parallel component of the pick-up ions velocity. The freshly
injected PUIs will be slipping with respect to the bulk flow and tend
to accumulate in the regions where B is
perpendicular to the flow. This situation may be represented by an
injection with a broadened delta peak.
Also, as discussed by Zank & Cairns (2000), the
wave excitation during the pick-up in quasi-perpendicular magnetic field
is less efficient than expected. However, the effect on our results would
be probably restricted to the low energy part of the spectrum, and the
results for the energies significantly higher than the initial spectrum
width would not be changed.
The pick-up ion spectra are obtained by numerical
integration of the above mentioned SDE-system of linear differential
equations and reflect the effects of convection, adiabatic cooling, and
momentum diffusion. We use the phase-space pick-up ion distribution
function
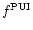 defined by
defined by
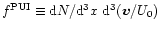 where
where 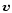 is the
particle velocity relative to plasma and
is the
particle velocity relative to plasma and
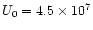 cms-1 is the
reference solar wind speed. The results from SDE calculations
by Chalov, Fahr & Izmodenov (Chalov et al. 1995) are
expressed in terms of
cms-1 is the
reference solar wind speed. The results from SDE calculations
by Chalov, Fahr & Izmodenov (Chalov et al. 1995) are
expressed in terms of
![$\Phi^{\rm PUI}\equiv U_0 [{\rm d}N/{\rm d}^3x\ {\rm d}(E/E_0)]$](/articles/aa/full/2001/44/aah2973/img44.gif) (
(
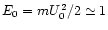 keV/n) which has the dimension of the differential flux (it is
approximately equal to the pick-up ion differential flux integrated
over the direction of particle velocity).
keV/n) which has the dimension of the differential flux (it is
approximately equal to the pick-up ion differential flux integrated
over the direction of particle velocity).
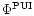 is
related to
is
related to
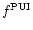 by:
by:
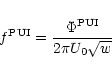 |
(5) |
where w denotes the normalized particle kinetic
energy in the plasma frame:
w=(v/U0)2=(E/E0).
In Fahr & Lay (2000) the calculations were restricted to
the upwind direction (i.e. 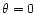 ). The numerical results for
). The numerical results for
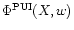 (where
(where
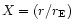 ,
,
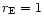 AU) in the
pre-shock range
AU) in the
pre-shock range
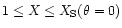 (
(
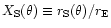 is the normalized
distance to the termination shock) can be parametrized in the form:
is the normalized
distance to the termination shock) can be parametrized in the form:
![\begin{displaymath}\Phi^{\rm PUI}(X,w)=C_{\gamma}(X) w^{\gamma} {\rm e}^{-[C_K(X)(w-w_0)^K]}
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img54.gif) |
(6) |
with
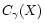 ,
CK(X), K,
,
CK(X), K, 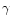 ,
and w0 defined
below. This corresponds to the following expression for the distribution
function:
,
and w0 defined
below. This corresponds to the following expression for the distribution
function:
![\begin{displaymath}f^{\rm PUI}_1(r,\theta=0,v)=\frac{
C_{\gamma}(X) w^{\gamma} {\rm e}^{-[C_K(X)(w-w_0)^K]}
}{2\pi U_0 \sqrt{w}}\cdot
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img57.gif) |
(7) |
Here the subscript "1'' denotes the preshock spectrum.
We consider two different cases, corresponding to different
behaviours of the Alfvenic turbulence with the distance from the Sun:
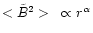 ,
where
,
where 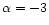 or -2(Chalov et al. 1995). The first case (
or -2(Chalov et al. 1995). The first case (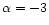 ,
dissipationless wave propagation) is appropriate to solar minimum
conditions (low turbulence). In this case the numerical results are best
fitted by the following parameters
,
dissipationless wave propagation) is appropriate to solar minimum
conditions (low turbulence). In this case the numerical results are best
fitted by the following parameters
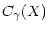 |
= |
![$\displaystyle 10^{4.3141}X^{-0.3363}\
[{\rm cm}^{-2}~{\rm s}^{-1}{\rm ~keV}^{-1}]$](/articles/aa/full/2001/44/aah2973/img60.gif) |
|
| CK(X) |
= |
0.442 X0.202 |
|
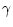 |
= |
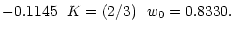 |
(8) |
The other case (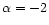 )
includes wave generation in interplanetary
space and leads to the fit parameters:
)
includes wave generation in interplanetary
space and leads to the fit parameters:
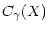 |
= |
![$\displaystyle 10^{4.1613}X^{-1.2567}\
[{\rm cm}^{-2}~{\rm s}^{-1}{\rm ~keV}^{-1}]$](/articles/aa/full/2001/44/aah2973/img63.gif) |
|
| CK(X) |
= |
0.469 X-0.5741 |
|
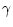 |
= |
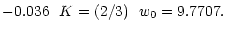 |
(9) |
It should be noted that while the first case ( )
corresponds
to the average energy of the pick-up ions of the order of 2 keV at large
distance, so that the total energy in the pick-up ions is not larger
than 0.3-0.5 of the solar wind kinetic and thermal energy, the case
)
corresponds
to the average energy of the pick-up ions of the order of 2 keV at large
distance, so that the total energy in the pick-up ions is not larger
than 0.3-0.5 of the solar wind kinetic and thermal energy, the case
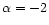 is unrealistic: the average energy of the pick-up ion
obtained from the resulting distribution function in
this case may be as high as 100 keV. In this case too much
energy is transferred from waves to the pick-up ions. Nevertheless, in the
following we present some of the results obtained with
is unrealistic: the average energy of the pick-up ion
obtained from the resulting distribution function in
this case may be as high as 100 keV. In this case too much
energy is transferred from waves to the pick-up ions. Nevertheless, in the
following we present some of the results obtained with 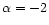 using
them as an illustration of an extreme case.
using
them as an illustration of an extreme case.
Our results are based on a simplified approach, in which the effect of
wave driving by the PUIs was neglected.
The studies of MHD turbulence behaviour in the outer
heliosphere carried out by Zank et al. (1996) and Matthaeus et
al. (1999), with the effects of mode mixing, driving by
stream-stream interactions and wave excitation by interplanetary pick-up
ions included in approximate form, produce the values
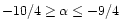 .
To extend our approach to these cases
would require including wave-driving in the transport equation from which
the pick-up ions distribution function is derived.
.
To extend our approach to these cases
would require including wave-driving in the transport equation from which
the pick-up ions distribution function is derived.
Figures 1 and 2 present the evolution of the PUI distribution function
with the distance in the upwind direction for these two cases together
with the corresponding post-shock distribution functions (see Sect. 3).
Our aim is now to generalize these results, derived for the upwind
(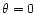 )
axis, to the general inecliptic regions with longitude angles
)
axis, to the general inecliptic regions with longitude angles
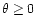 .
Instead of solving Eq. (2) for the non-spherically-symmetric case we shall
assume that the distribution function can be derived from the solution for
the upwind direction by a simple re-scaling with a direction dependent
correction factor
.
Instead of solving Eq. (2) for the non-spherically-symmetric case we shall
assume that the distribution function can be derived from the solution for
the upwind direction by a simple re-scaling with a direction dependent
correction factor
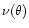 :
:
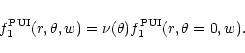 |
(10) |
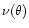 is determined by requiring that the resulting
distribution reproduces the directional dependence of the pick-up
ion number density at some reference distance. This approach requires the
assumption that the interplanetary turbulence levels determining the
momentum diffusion coefficients
is determined by requiring that the resulting
distribution reproduces the directional dependence of the pick-up
ion number density at some reference distance. This approach requires the
assumption that the interplanetary turbulence levels determining the
momentum diffusion coefficients
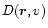 within the ecliptic
only depend on the solar distance r, but not on longitude
within the ecliptic
only depend on the solar distance r, but not on longitude
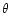 .
Momentum diffusion thus operates independent of longitude.
.
Momentum diffusion thus operates independent of longitude.
The correction factor
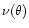 is given by
is given by
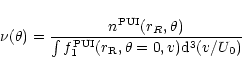 |
(11) |
where 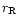 is some reference distance (we take
is some reference distance (we take
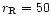 AU),
AU),
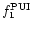 is given by Eq. (7), and
is given by Eq. (7), and
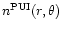 is
the pick-up ion number density at
is
the pick-up ion number density at
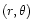 which we take from
the model of the heliosphere based on a gas-dynamical 5-fluid numerical
solution (Fahr et al. 2000) in which the pick-up protons were considered
as one of the component fluids. The same model is used to provide the
function
which we take from
the model of the heliosphere based on a gas-dynamical 5-fluid numerical
solution (Fahr et al. 2000) in which the pick-up protons were considered
as one of the component fluids. The same model is used to provide the
function
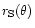 defining the
shape of the solar wind termination shock.
defining the
shape of the solar wind termination shock.
With the help of the
above formulae one can give the near ecliptic PUI upstream spectra for
longitudes
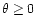 at the shock by
at the shock by
![$\displaystyle f^{\rm PUI}_1(r_{\rm S}(\theta),\theta,v)=\nu(\theta)\frac{
C_{\g...
...ta))w^{\gamma}
{\rm e}^{-[C_K(X_{\rm S}(\theta))(w-w_0)^K]}}
{2\pi U_0 w^{1/2}}$](/articles/aa/full/2001/44/aah2973/img76.gif) |
|
|
(12) |
where
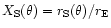 ,
w=(v/U0)2.
,
w=(v/U0)2.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{h2973f1.eps}\end{figure}](/articles/aa/full/2001/44/aah2973/Timg78.gif) |
Figure 1:
PUI distribution function evolution with distance
(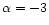 ). The functions for distances 5.0, 20.0 and 80.0 AU (apex
direction) are presented by dotted lines. The distribution immediately
downstream from the shock is shown by the solid line. (See Sect. 3). ). The functions for distances 5.0, 20.0 and 80.0 AU (apex
direction) are presented by dotted lines. The distribution immediately
downstream from the shock is shown by the solid line. (See Sect. 3). |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{h2973f2.eps} %
\end{figure}](/articles/aa/full/2001/44/aah2973/Timg79.gif) |
Figure 2:
PUI distribution function evolution with distance
(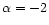 ). The functions for distances 5.0, 20.0 and 80.0 AU (apex
direction) are presented by dotted lines. The distribution immediately
downstream from the shock is shown by the solid line (see Sect. 3). ). The functions for distances 5.0, 20.0 and 80.0 AU (apex
direction) are presented by dotted lines. The distribution immediately
downstream from the shock is shown by the solid line (see Sect. 3). |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2973f3.eps}
\end{figure}](/articles/aa/full/2001/44/aah2973/Timg80.gif) |
Figure 3:
Preaccelerated pick-up proton spectra immediately downstream
from the termination shock (model predictions: Eq. (24)). The spectra
are shown for three positions on the surface of the shock:
 (apex),
(apex),  (side) and
(side) and 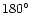 (antiapex) in the ecliptic plane.
The cases of normal (
(antiapex) in the ecliptic plane.
The cases of normal (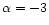 )
and high turbulence ( )
and high turbulence (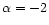 )
are presented. Also presented is the ACR spectrum at the shock derived
from de-modulation of the observed spectrum (Stone et al. 1996). )
are presented. Also presented is the ACR spectrum at the shock derived
from de-modulation of the observed spectrum (Stone et al. 1996). |


Up: Pick-up ions upstream and
Copyright ESO 2001
![]() ,
is found as a
solution of the following kinetic transport equation (see e.g. Lee
1983; Isenberg 1987; Bogdan et al.
1991):
,
is found as a
solution of the following kinetic transport equation (see e.g. Lee
1983; Isenberg 1987; Bogdan et al.
1991):
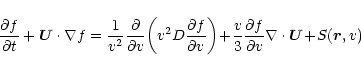
![]() .
This in effect
restricts our considerations to the vicinity
of the ecliptic plane. Using spherical polar coordinates
.
This in effect
restricts our considerations to the vicinity
of the ecliptic plane. Using spherical polar coordinates
![]() ,
with the Sun as the origin and the polar axis oriented to the interstellar
upwind direction (i.e.
,
with the Sun as the origin and the polar axis oriented to the interstellar
upwind direction (i.e.
![]() upwind direction), the above
transport equation (Eq. (1)) after introduction of the differential phase
space density,
upwind direction), the above
transport equation (Eq. (1)) after introduction of the differential phase
space density,
![]() attains the following form (see Chalov et al. 1997):
attains the following form (see Chalov et al. 1997):
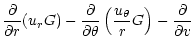
![$\displaystyle \!\!\left[\left(\frac{\partial D}{\partial v}+\frac{2D}{v}\frac{v...
...sin\theta}\frac{\partial u_{\theta}\sin\theta}{\partial
\theta}
\right)G\right]$](/articles/aa/full/2001/44/aah2973/img26.gif)
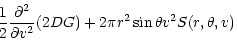
![]() is due to neutral H atoms which
become ionized at
is due to neutral H atoms which
become ionized at
![]() .
These neutral
LISM H atoms penetrate from interstellar space into the interface
region of perturbed solar wind and interstellar plasma flows and with
some depletion eventually appear in the inner heliosphere being subject
to ionization processes there. When these neutral atoms are ionized,
they constitute the H+-pick-up ion production rate
.
These neutral
LISM H atoms penetrate from interstellar space into the interface
region of perturbed solar wind and interstellar plasma flows and with
some depletion eventually appear in the inner heliosphere being subject
to ionization processes there. When these neutral atoms are ionized,
they constitute the H+-pick-up ion production rate
![]() .
The local heliospheric pick-up H+-production rate is
given by the following formula (see Rucinski et al. 1993):
.
The local heliospheric pick-up H+-production rate is
given by the following formula (see Rucinski et al. 1993):
![\begin{displaymath}q(\vec{r})=n_{\rm H}(\vec{r})[\nu_{\rm ph}(\vec{r})+\nu_{\rm ex}(\vec{r})]
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img33.gif)
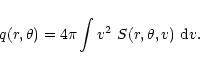
![]() defined by
defined by
![]() where
where ![]() is the
particle velocity relative to plasma and
is the
particle velocity relative to plasma and
![]() cms-1 is the
reference solar wind speed. The results from SDE calculations
by Chalov, Fahr & Izmodenov (Chalov et al. 1995) are
expressed in terms of
cms-1 is the
reference solar wind speed. The results from SDE calculations
by Chalov, Fahr & Izmodenov (Chalov et al. 1995) are
expressed in terms of
![]() (
(
![]() keV/n) which has the dimension of the differential flux (it is
approximately equal to the pick-up ion differential flux integrated
over the direction of particle velocity).
keV/n) which has the dimension of the differential flux (it is
approximately equal to the pick-up ion differential flux integrated
over the direction of particle velocity).
![]() is
related to
is
related to
![]() by:
by:
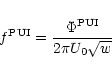
![]() ). The numerical results for
). The numerical results for
![]() (where
(where
![]() ,
,
![]() AU) in the
pre-shock range
AU) in the
pre-shock range
![]() (
(
![]() is the normalized
distance to the termination shock) can be parametrized in the form:
is the normalized
distance to the termination shock) can be parametrized in the form:
![\begin{displaymath}\Phi^{\rm PUI}(X,w)=C_{\gamma}(X) w^{\gamma} {\rm e}^{-[C_K(X)(w-w_0)^K]}
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img54.gif)
![\begin{displaymath}f^{\rm PUI}_1(r,\theta=0,v)=\frac{
C_{\gamma}(X) w^{\gamma} {\rm e}^{-[C_K(X)(w-w_0)^K]}
}{2\pi U_0 \sqrt{w}}\cdot
\end{displaymath}](/articles/aa/full/2001/44/aah2973/img57.gif)
![]() ,
where
,
where ![]() or -2(Chalov et al. 1995). The first case (
or -2(Chalov et al. 1995). The first case (![]() ,
dissipationless wave propagation) is appropriate to solar minimum
conditions (low turbulence). In this case the numerical results are best
fitted by the following parameters
,
dissipationless wave propagation) is appropriate to solar minimum
conditions (low turbulence). In this case the numerical results are best
fitted by the following parameters
![]() .
To extend our approach to these cases
would require including wave-driving in the transport equation from which
the pick-up ions distribution function is derived.
.
To extend our approach to these cases
would require including wave-driving in the transport equation from which
the pick-up ions distribution function is derived.
![]() )
axis, to the general inecliptic regions with longitude angles
)
axis, to the general inecliptic regions with longitude angles
![]() .
Instead of solving Eq. (2) for the non-spherically-symmetric case we shall
assume that the distribution function can be derived from the solution for
the upwind direction by a simple re-scaling with a direction dependent
correction factor
.
Instead of solving Eq. (2) for the non-spherically-symmetric case we shall
assume that the distribution function can be derived from the solution for
the upwind direction by a simple re-scaling with a direction dependent
correction factor
![]() :
:
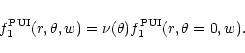
![]() is given by
is given by
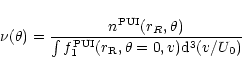
![]() at the shock by
at the shock by
![$\displaystyle f^{\rm PUI}_1(r_{\rm S}(\theta),\theta,v)=\nu(\theta)\frac{
C_{\g...
...ta))w^{\gamma}
{\rm e}^{-[C_K(X_{\rm S}(\theta))(w-w_0)^K]}}
{2\pi U_0 w^{1/2}}$](/articles/aa/full/2001/44/aah2973/img76.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{h2973f3.eps}
\end{figure}](/articles/aa/full/2001/44/aah2973/Timg80.gif)