

Up: BI Lyncis: A hydrogen-deficient G
Subsections
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F2.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg27.gif) |
Figure 2:
Ultraviolet and visual spectrophotometry of BI Lyn
(histogram) together with the best fitting theoretical flux distribution
(polyline and horizontal bars).
The latter represents the sum of two model atmospheres (dashed
lines) with effective temperature and angular radii
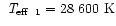 , ,
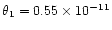 rad,
rad,
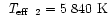 and
and
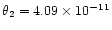 rad. Interstellar reddening is negligible.
rad. Interstellar reddening is negligible.
|
The available spectra of BI Lyn suggest that it comprises a hot helium-rich
source and a cooler source since we see absorption lines due to plasma in
two quite different ionization states. In constructing a model to fit
these spectra, a number of assumptions - or approximations - influence
our conclusions. Many of these
are necessary because both the number of free parameters and the limited
number of constraints preclude an exhaustive search of solution space.
The fundamental assumption is that both cool and
hot absorption sources are primarily stellar. This seems to
hold well for the hot source. This remains a good working hypothesis
even though high rotational broadening in the cool
source spectrum and the presence of H emission makes a purely
stellar identification less secure.
emission makes a purely
stellar identification less secure.
For two stellar sources, the principal free parameters which govern
the measured spectrum are as follows (subscripts refer to the hot
and cool source respectively):
-
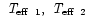 :
effective temperature,
:
effective temperature,
-
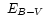 :
interstellar extinction,
:
interstellar extinction,
-
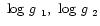 :
surface gravity,
:
surface gravity,
-
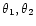 :
angular diameter providing the relative radii
R2/R1,
:
angular diameter providing the relative radii
R2/R1,
-
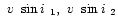 :
rotational velocity,
:
rotational velocity,
- v1, v2: radial velocity,
-
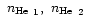 :
helium abundance,
:
helium abundance,
-
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_1, \mbox{~${\rm [\beta_{\rm Fe}]}$ }_2$](/articles/aa/full/2001/42/aah2958/img34.gif) :
metallicity
:
metallicity![[*]](/icons/foot_motif.gif) ,
,
-
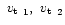 :
microturbulent velocity.
:
microturbulent velocity.
Ideally, stellar composition entails many more free parameters than
metallicity and helium abundance alone, but requires high-resolution
spectroscopy to measure, as does the microturbulent
velocity.
Helium abundance cannot be measured directly for cool sources.
Tests showed that
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_2$](/articles/aa/full/2001/42/aah2958/img46.gif) cannot be uniquely determined from the given data.
Similarly, given the magnitude of errors in
cannot be uniquely determined from the given data.
Similarly, given the magnitude of errors in
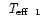 ,
it is not practical to measure
,
it is not practical to measure
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_1$](/articles/aa/full/2001/42/aah2958/img48.gif) in detail.
in detail.
Thus the second group of assumptions are as follows.
The abundances of all elements other than hydrogen and helium are
in proportion to their cosmic abundances, with
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_1 = \mbox{~${\rm [\beta_{\rm Fe}]}$ }_2 = 0$](/articles/aa/full/2001/42/aah2958/img49.gif) .
The helium abundance of the
cool star is normal:
.
The helium abundance of the
cool star is normal:
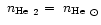 .
The adopted microturbulent velocities are typical for early-type stars
.
The adopted microturbulent velocities are typical for early-type stars
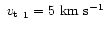 and main-sequence late-type stars
and main-sequence late-type stars
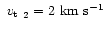 .
The latter assumption is very important as it affects both the
metallicity
.
The latter assumption is very important as it affects both the
metallicity
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_2$](/articles/aa/full/2001/42/aah2958/img46.gif) (see above) and the derived
radius ratio R2/R1. We have adopted
(see above) and the derived
radius ratio R2/R1. We have adopted
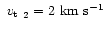 in order
that the latter quantity as derived from spectral fitting be as consistent
as possible with
in order
that the latter quantity as derived from spectral fitting be as consistent
as possible with
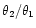 derived from spectrophotometry
where we have also used cool star models computed with
derived from spectrophotometry
where we have also used cool star models computed with
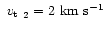 .
Secondary effects on
.
Secondary effects on
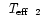 and
and
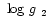 are
not significant here.
are
not significant here.
The third level of assumptions concerns the physics.
The stars are assumed to be spherically symmetric
and not to vary significantly over time. The approximations of
plane-parallel geometry, local thermodynamic, radiative and
hydrostatic equilibrium have been assumed valid for modelling
their atmospheres (rapid rotation and H emission may
compromise these).
emission may
compromise these).
However, with these assumptions and approximations, it becomes
possible, in principle, to solve for the remaining 12 (!) free parameters
by modelling the overall flux distribution and the intermediate-resolution
spectra of BI Lyn.
The methods for fitting flux distributions and high-resolution spectra
by least-squares minimization within grids of models have been
described in detail elsewhere (Jeffery et al. 2001). The primary codes used
are BINFIT and SFIT.
BINFIT is an extension of the
single star code TFIT used to model the flux distribution of a
binary system containing a hot and a cool star. Fitting of each
component is done within a one-dimensional grid, normally
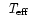 ,
convolved with an extinction curve
,
convolved with an extinction curve
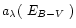 and angular
radius
and angular
radius  .
The flux distributions used in the model grids are of
low resolution and taken directly from the output of LTE model atmosphere
codes STERNE (Jeffery et al. 2001) or ATLAS (Kurucz 1979).
.
The flux distributions used in the model grids are of
low resolution and taken directly from the output of LTE model atmosphere
codes STERNE (Jeffery et al. 2001) or ATLAS (Kurucz 1979).
SFIT is used to model intermediate and high-resolution stellar spectra
by interpolation in three-dimensional model grids, normally
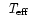 ,
,
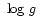 and an abundance parameter, e.g.
and an abundance parameter, e.g.
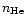 or
or
![${\rm [\beta_{\rm Fe}]}$](/articles/aa/full/2001/42/aah2958/img61.gif) .
Versions
exist for both single and binary stars, and appropriate allowance
is made for velocity shifts, rotational broadening, and instrumental
broadening. Given the relative radii of stars in a binary, the
spectra are added correctly at the absolute flux level and then
normalized to the true total continuum. Provision is made to renormalize
the observed spectrum to the true continuum in order to optimize the
fit. SFIT may be used to measure any or all of
.
Versions
exist for both single and binary stars, and appropriate allowance
is made for velocity shifts, rotational broadening, and instrumental
broadening. Given the relative radii of stars in a binary, the
spectra are added correctly at the absolute flux level and then
normalized to the true total continuum. Provision is made to renormalize
the observed spectrum to the true continuum in order to optimize the
fit. SFIT may be used to measure any or all of
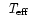 ,
,
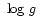 ,
abundance,
,
abundance,
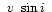 ,
and R2/R1. In practise,
only two or three variables should be solved for simultaneously,
although R2/R1 should always be a free parameter. Consequently,
the use of SFIT is iterative, particularly for binaries.
,
and R2/R1. In practise,
only two or three variables should be solved for simultaneously,
although R2/R1 should always be a free parameter. Consequently,
the use of SFIT is iterative, particularly for binaries.
The radial velocity shifts v may be found by cross-correlating
the observed spectrum with individual components of a synthetic
spectrum which is a sufficiently good approximation to the final
solution. Providing the
hot and cool star spectra are sufficiently different, cross-correlation
will automatically identify the individual components in the observed
spectrum, although it is important to exclude strong features present
in both spectra (e.g. Balmer lines).
The model atmospheres and flux distributions used to analyse the
hot star are computed with the plane-parallel LTE code STERNE,
which is adapted for dealing with hydrogen-deficient stellar atmospheres.
The high-resolution spectra are calculated with the LTE code
SPECTRUM. Both codes are described more fully by Jeffery et al.
(2001).
Model atmospheres used in this investigation were calculated on a
three-dimensional rectangular grid defined
by
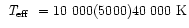 ,
,
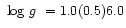 ,
and composition
,
and composition
![$[\mbox{~$n_{\rm H}$ },\mbox{~$n_{\rm He}$ },\mbox{~${\rm [\beta_{\rm Fe}]}$ }] = [0.0,1.0,0.0]$](/articles/aa/full/2001/42/aah2958/img65.gif) ,
[0.01,0.99,0.0],
[0.05,0.95,0.0]and
[0.1,0.9,-1.0]. The larger value of
,
[0.01,0.99,0.0],
[0.05,0.95,0.0]and
[0.1,0.9,-1.0]. The larger value of 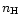 or
or
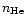 is reduced to
compensate for the trace elements. Coarse model grids for
is reduced to
compensate for the trace elements. Coarse model grids for
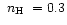 ,
0.5, 0.7, 0.9, 0.95, 0.99 and 1.0, with corresponding
,
0.5, 0.7, 0.9, 0.95, 0.99 and 1.0, with corresponding
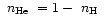 and
and
![${\rm [\beta_{\rm Fe}]}$](/articles/aa/full/2001/42/aah2958/img61.gif) ,
are also available, as are fine grids with
,
are also available, as are fine grids with
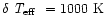 and
and
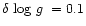 for selected areas of (
for selected areas of (
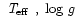 )
space.
)
space.
Synthetic spectra were calculated on wavelength intervals
3900-5000 Å (blue),
6360-6770 Å (red/H )
and
8400-8800 Å (CaT). Linelists were
taken from the list of assessed data for hot stars LTE/_LINES
(Jeffery 1991). Microturbulent velocity
)
and
8400-8800 Å (CaT). Linelists were
taken from the list of assessed data for hot stars LTE/_LINES
(Jeffery 1991). Microturbulent velocity
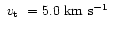 and solar abundances for
all elements other than hydrogen and helium were assumed (see above).
and solar abundances for
all elements other than hydrogen and helium were assumed (see above).
Model atmospheres and flux distributions used to analyse the cool star
were taken from the Kurucz' standard grid of ATLAS models (Kurucz 1993),
for
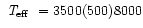 ,
,
 ,
,
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }=-0.5, -0.3, 0.0$](/articles/aa/full/2001/42/aah2958/img75.gif) and
and
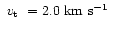 .
.
High resolution spectra were calculated in the same spectral regions as
for the hot star using Kurucz' code SYNTHE
(Kurucz 1991; Jeffery et al. 1996). Grids with microturbulent velocities
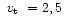 and 10.0
and 10.0
 were computed.
were computed.
The method for measuring T
 and angular radii
and angular radii  for both components in
composite systems containing a hot subdwarf and a cool companion using IUE
spectrophotometry and optical-IR broad-band photometry has been described
elsewhere (Aznar Cuadrado & Jeffery 2001). In fact PG0900+400 appeared in the sample analyzed,
yielding
for both components in
composite systems containing a hot subdwarf and a cool companion using IUE
spectrophotometry and optical-IR broad-band photometry has been described
elsewhere (Aznar Cuadrado & Jeffery 2001). In fact PG0900+400 appeared in the sample analyzed,
yielding
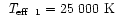 ,
,
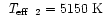 ,
with
R2/R1=8.0.
However it had been assumed that
,
with
R2/R1=8.0.
However it had been assumed that
 and
and
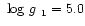 .
For this paper, the data were re-analyzed iteratively with the optical data
(see below). Consequently, quite different model atmosphere grids were
adopted in the final analysis, with
.
For this paper, the data were re-analyzed iteratively with the optical data
(see below). Consequently, quite different model atmosphere grids were
adopted in the final analysis, with
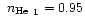 and
and
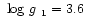 .
Interstellar
extinction was still found to be negligible, but the different distribution of
opacity in the hydrogen-deficient atmosphere of the hot star resulted in a higher T
.
Interstellar
extinction was still found to be negligible, but the different distribution of
opacity in the hydrogen-deficient atmosphere of the hot star resulted in a higher T
 being obtained for both components.
being obtained for both components.
With
 ,
the earlier measurement of
,
the earlier measurement of 
 (Ferguson et al. 1984) was approximately recovered.
However, with
(Ferguson et al. 1984) was approximately recovered.
However, with
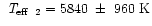 ,
the cool star appears to be somewhat hotter than the K3 spectral type
indicated
before. The broader spectral range covered by our data should lead to a
more robust result than the flux ratio method (Wade 1980). It is
noted that the errors are formal errors and do not allow for systematic errors as
may be introduced, for example, by an inappropriate choice for
unconstrained model atmosphere parameters.
The relative radii of the two stars, given by their angular diameters, is
,
the cool star appears to be somewhat hotter than the K3 spectral type
indicated
before. The broader spectral range covered by our data should lead to a
more robust result than the flux ratio method (Wade 1980). It is
noted that the errors are formal errors and do not allow for systematic errors as
may be introduced, for example, by an inappropriate choice for
unconstrained model atmosphere parameters.
The relative radii of the two stars, given by their angular diameters, is
 .
Other parameters of the fit are given in Table 3.
The best-fit model flux distribution is shown together with the data in
Fig. 2.
.
Other parameters of the fit are given in Table 3.
The best-fit model flux distribution is shown together with the data in
Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F3.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg103.gif) |
Figure 3:
Normalized blue spectrum of BI Lyn (bottom: d)) together
with a best fit composite model spectrum c) formed by adding models with
a)
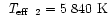 , ,
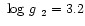 , ,
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_2=0.00$](/articles/aa/full/2001/42/aah2958/img102.gif) (top) and
b)
(top) and
b)
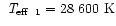 , ,
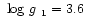 , ,
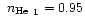 assuming that the relative radii
R2/R1=4.9. The model spectra have been
velocity shifted and degraded to match the observed spectral resolution
(1 Å) (WHT images: 337312 + 337313 + 337318 + 337319 + 337416 + 337418 + 337419).
A detailed comparison between the observed spectrum and best-fit model
is shown in Fig. 4.
assuming that the relative radii
R2/R1=4.9. The model spectra have been
velocity shifted and degraded to match the observed spectral resolution
(1 Å) (WHT images: 337312 + 337313 + 337318 + 337319 + 337416 + 337418 + 337419).
A detailed comparison between the observed spectrum and best-fit model
is shown in Fig. 4.
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F4.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg104.gif) |
Figure 4:
Normalized blue spectrum of BI Lyn (histogram)
together with the best fit composite model spectrum (polyline: see Fig. 3c)
showing the fit in detail.
|
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F5.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg105.gif) |
Figure 5:
As Fig. 3 in the region of the
infared calcium triplet (INT image: 155728). |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F6.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg106.gif) |
Figure 6:
As Fig. 3 in the region of H (WHT images: 337414 + 337415 + 337417).
(WHT images: 337414 + 337415 + 337417). |
Much more information is available in the line spectrum than can be obtained
from photometry alone. The object of spectrum synthesis is to find, given
assumptions that have been introduced already, a model for the overall spectrum
that best matches the observation by, for example, minimizing the square
of residuals between model and data. Techniques for doing this with
single stars have been described already (Jeffery et al. 2001). The extension to
binary stars has been developed by Aznar Cuadrado & Jeffery (in preparation)
and described by Aznar Cuadrado (Aznar Cuadrado 2001).
Under perfect conditions (e.g. noise-free data),
a residual-minimization procedure could solve for many free
parameters simultaneously. In practice, it is necessary to hold most parameters fixed
while solving for two or three at a time, and iterating around several parameters
until an optimum solution is obtained. With the assumptions introduced
already, the final solution for BI Lyn is
given in Table 3. The errors cited in fitted quantities are
formal errors from the 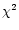 minimization. Other errors have been
propagated from these. Systematic errors
(e.g. choice of
minimization. Other errors have been
propagated from these. Systematic errors
(e.g. choice of
![${\rm [\beta_{\rm Fe}]}$](/articles/aa/full/2001/42/aah2958/img61.gif) ,
,
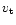 )
can significantly affect these.
)
can significantly affect these.
A free spectroscopic solution for effective temperature gave
 kK, but could not provide
kK, but could not provide
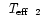 because
of a lack of temperature-sensitive diagnostics.
To maintain consistency in the radius ratio, the spectrophotometric
solutions for
because
of a lack of temperature-sensitive diagnostics.
To maintain consistency in the radius ratio, the spectrophotometric
solutions for
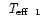 and
and
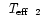 were retained.
were retained.
The surface gravity and helium abundance of the hot star were
well determined spectroscopically; there is negligible rotational
broadening (at the instrumental resolution) in the line profiles.
It is clear that the hot component is a hydrogen-deficient giant
with
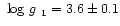 with an atmosphere containing some 5 per cent
hydrogen and 95 per cent helium (by number).
with an atmosphere containing some 5 per cent
hydrogen and 95 per cent helium (by number).
The cool star is more difficult to analyse, mainly because of substantial
rotation broadening
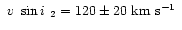 .
Metallicity, microturbulent
velocity, helium abundance and gravity all affect the strength of
the metal line spectrum, which is then heavily smeared by the rotation.
The infrared calcium triplet could provide a good gravity indicator
if
.
Metallicity, microturbulent
velocity, helium abundance and gravity all affect the strength of
the metal line spectrum, which is then heavily smeared by the rotation.
The infrared calcium triplet could provide a good gravity indicator
if
![${\rm [\beta_{\rm Fe}]}$](/articles/aa/full/2001/42/aah2958/img61.gif) were known. Assuming
were known. Assuming
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }_2=0.0$](/articles/aa/full/2001/42/aah2958/img112.gif) we find
we find
 .
.
With the assumptions given and parameters deduced, a free solution gives
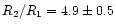 in both blue and infared spectral regions. This is
determined solely by the strength of the cool star absorption spectrum,
so is clearly assumption dependent. Given the nature of these, it is
satisfactory that R2/R1 is within 40% of the value obtained from
photometry.
in both blue and infared spectral regions. This is
determined solely by the strength of the cool star absorption spectrum,
so is clearly assumption dependent. Given the nature of these, it is
satisfactory that R2/R1 is within 40% of the value obtained from
photometry.
The best-fit model spectra for both hot and cool stars, their sum according
to the given relative radii and a comparison with the observed spectrum
are given for all spectra regions in Figs. 3-6.
Given the measured dimensions of BI Lyn, a number of other properties
including masses, luminosities and distance may be estimated.
However these depend on which value for R2/R1 is adopted, an estimate
for the hot star mass M1 and the quality of the
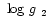 measurement.
Possible values, given choices for each of these parameters, are shown in
Table 4. The given distance is derived from the measured
angular diameter and the derived radius of the cool star (
measurement.
Possible values, given choices for each of these parameters, are shown in
Table 4. The given distance is derived from the measured
angular diameter and the derived radius of the cool star (
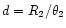 ).
A similar result is obtained from the apparent visual magnitude and derived
luminosities.
).
A similar result is obtained from the apparent visual magnitude and derived
luminosities.
These solutions must be reconciled with the position
of BI Lyn which, with
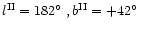 ,
is substantially (
,
is substantially (
 3 kpc) out of the Galactic plane in the
anticentre direction. It therefore seems preferable to seek the lowest
possible mass for the cool star in which case
a solution with
3 kpc) out of the Galactic plane in the
anticentre direction. It therefore seems preferable to seek the lowest
possible mass for the cool star in which case
a solution with
 and
and
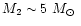 is indicated. The latter is comparable with the
companion star mass estimated for another hydrogen-deficient binary
-
is indicated. The latter is comparable with the
companion star mass estimated for another hydrogen-deficient binary
- 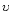 Sgr (Schönberner & Drilling 1983; Dudley & Jeffery 1990).
Sgr (Schönberner & Drilling 1983; Dudley & Jeffery 1990).
A better solution might be achieved if we have overestimated g2 by, for
example, placing the continuum around the infrared calcium triplet
too low or underestimating the hot star flux at these wavelengths.
With
 and
and
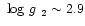 or 2.5, a cool star
mass
or 2.5, a cool star
mass
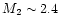 or 1
or 1 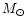 would be easier to reconcile with the Galactic
position.
would be easier to reconcile with the Galactic
position.
In any event, the components must be highly evolved. A solution
comprising a 0.5 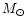 B-type helium star and a 1-5
B-type helium star and a 1-5 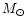 G-type
giant (luminosity class II - III) is consistent with the
observational data presented in this paper. It is suggested that
BI Lyn is a post common-envelope binary in which the primary
(helium star) has almost completely shed its outer hydrogen-rich
envelope together with substantial angular momentum. A large fraction
of this has been transferred to the cooler star. The envelope of the
cool star may not yet be in thermal equilibrium - there may still be
a main-sequence star underneath giving it the semblance of a giant.
This would account for the apparently advanced evolutionary state of
the cool star at the same time as the hot star is in a relatively
short-lived phase of evolution.
G-type
giant (luminosity class II - III) is consistent with the
observational data presented in this paper. It is suggested that
BI Lyn is a post common-envelope binary in which the primary
(helium star) has almost completely shed its outer hydrogen-rich
envelope together with substantial angular momentum. A large fraction
of this has been transferred to the cooler star. The envelope of the
cool star may not yet be in thermal equilibrium - there may still be
a main-sequence star underneath giving it the semblance of a giant.
This would account for the apparently advanced evolutionary state of
the cool star at the same time as the hot star is in a relatively
short-lived phase of evolution.
The surface gravity for the hot star places it on an evolutionary
track for a post-AGB star of 
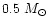 (Schönberner 1983).
(Schönberner 1983).
The referee has rightly pointed out that the detailed results of
our analysis are subject to the LTE assumption used in the analysis of
the early-type star. Being a giant, departures from LTE can be
significant and will affect, in particular,
the predicted equivalent widths of the He I lines. Other
spectral features may also be affected. Non-LTE calculations for
hydrogen-poor hydrogen-helium atmospheres have been available for some
years, but fully line-blanketed NLTE models for hydrogen-poor atmospheres
with
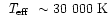 have not yet been successfully
computed (Rauch 1996). Their eventual arrival will affect the
detailed results presented here but not the overall conclusions
concerning the dimensions of BI Lyn.
have not yet been successfully
computed (Rauch 1996). Their eventual arrival will affect the
detailed results presented here but not the overall conclusions
concerning the dimensions of BI Lyn.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F7.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg125.gif) |
Figure 8:
Residuals of four spectra with respect to the mean
WHT spectrum in the region of H ,
labelled by image number.
Only the INT spectrum shows a significant change in the absorption strength. ,
labelled by image number.
Only the INT spectrum shows a significant change in the absorption strength. |


Up: BI Lyncis: A hydrogen-deficient G
Copyright ESO 2001
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F2.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F3.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg103.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F4.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F5.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg105.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F6.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{H2958_F7.PS}
\end{figure}](/articles/aa/full/2001/42/aah2958/Timg125.gif)