- ... G
![[*]](/icons/foot_motif.gif)
- Based on observations obtained with the
Isaac Newton and William Herschel Telescopes,
and on INES data from the IUE satellite.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... metallicity
![[*]](/icons/foot_motif.gif)
-
The measurement of chemical abundance from a spectral line normally
provides the number fraction (n) relative to the continuous opacity source which,
in most stars, is hydrogen.
The metallicity of a star may then be given as the logarithm of
the ratio of the iron-to-hydrogen fraction (
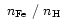 )
relative to
that in the Sun:
)
relative to
that in the Sun:
![$\mbox{~${\rm [Fe/H]}$ }\equiv \log ((\mbox{~$n_{\rm Fe}$ }/\mbox{~$n_{\rm H}$ }) / (\mbox{~$n_{\rm Fe}$ }/\mbox{~$n_{\rm H}$ })_\odot)$](/articles/aa/full/2001/42/aah2958/img36.gif) .
Thus
.
Thus
![$\mbox{~${\rm [Fe/H]}$ }=-0.3$](/articles/aa/full/2001/42/aah2958/img37.gif) implies one half of the solar metallicity,
assuming that the relative abundances of species heavier than helium
follow some cosmic norm. These conventions break down
for hydrogen-deficient stars, where nucleosynthesis has replaced hydrogen
with helium and other heavy elements, and continuous opacity is provided
by other species. In some cases, it makes sense
to cite fractional abundance by number relative to the total number of
ions in the plasma (e.g.
implies one half of the solar metallicity,
assuming that the relative abundances of species heavier than helium
follow some cosmic norm. These conventions break down
for hydrogen-deficient stars, where nucleosynthesis has replaced hydrogen
with helium and other heavy elements, and continuous opacity is provided
by other species. In some cases, it makes sense
to cite fractional abundance by number relative to the total number of
ions in the plasma (e.g.
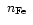 ). Where this is done for normal stars,
the logarithm
is taken and an arbitrary constant c added to make the hydrogen abundance
). Where this is done for normal stars,
the logarithm
is taken and an arbitrary constant c added to make the hydrogen abundance
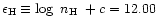 .
This number can be used
in stars where hydrogen is replaced by helium, but the constant
must be modified to reflect the change in mass fractions of H, He and possibly
other species.
Mass fractions (
.
This number can be used
in stars where hydrogen is replaced by helium, but the constant
must be modified to reflect the change in mass fractions of H, He and possibly
other species.
Mass fractions (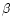 )
provide a more convenient measure because
they are conserved when other species transmute, but they are less often used
in the literature.
For this paper we adopt the convention
)
provide a more convenient measure because
they are conserved when other species transmute, but they are less often used
in the literature.
For this paper we adopt the convention
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }= \log (\beta_{\rm Fe} / \beta_{\rm Fe \odot}) $](/articles/aa/full/2001/42/aah2958/img41.gif) to refer to the
mass fraction of iron relative to that in the Sun. Thus
to refer to the
mass fraction of iron relative to that in the Sun. Thus
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }=0.0$](/articles/aa/full/2001/42/aah2958/img42.gif) correctly implies a solar metallicity, regardless of the
abundances of transmuted elements. For normal stars,
correctly implies a solar metallicity, regardless of the
abundances of transmuted elements. For normal stars,
![$\mbox{~${\rm [\beta_{\rm Fe}]}$ }\equiv\mbox{~${\rm [Fe/H]}$ }$](/articles/aa/full/2001/42/aah2958/img43.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.