3 Results and discussion

3.1 The updated PMS ${e-log\,P}$ diagram and the new PMS circularization period

An updated version of the PMS $e-\log P$ diagram is shown in Fig. 2. Circles stand for double-lined spectroscopic binary (SB2) systems and triangles stand for single-lined spectroscopic binary (SB1) systems. Those SB systems where at least one of the components has a mass clearly outside the range explored by Zahn & Bouchet (1989), i.e. from 0.5 to $1.5~M_\odot$, are shown as open symbols.

 

 

Table 3: Orbital period and eccentricity for the known PMS spectroscopic binaries. When possible, information about the spectral type of the components is given. Spatial location and the respective reference are also indicated.

Star	Period	e	Spectral Type	Location	Reference
	(days)		(Primary+Secondary)
HD 1555552	1.68	0	G5+K1	Isolated	Pasquini et al. (1991)
RS Cha2	1.67	0	$^\dag$A8+A8	Cha	Andersen (1975)
V4046Sgr2	2.42	0	K5+K7	Isolated	de la Reza et al. (1986)
155913-22331	2.42	0	K5	Sco-Cen	Mathieu et al. (1989)
TY CrA2,3	2.89	0	$^\dag$B9	Corona Aus	Casey et al. (1993)
RX J0529.4+00412	3.03	0	K1+K7	Orion	Covino et al. (2000)
V826Tau2	3.88	0	K8+K8	Tau-Aur	Reipurth et al. (1990)
OriNTT5692	4.25	0	K4	Orion Belt	Mathieu (1994)
RX J0541.4-03242	4.98	0	G8+K3	Orion	Covino et al. (2001a)
EKCep2	4.42	0.11	$^\dag$A1+G5	Isolated	Tomkin (1983)
P24862	5.19	0.16	G5	Trapezium	Mathieu (1994)
W1342	6.35	0	$^\dag$G5+G7	NGC2264	Padgett & Stapelfeldt (1994)
OriNTT4292	7.46	0.27	K3	Orion Belt	Mathieu (1994)
RX J1603.9-39382	7.56	0	K2+K3	Lupus	This paper; Guenther et al. (2001)
160905-18591	10.40	0.17	K1	Sco-Cen	Mathieu et al. (1989)
VSB1261	12.92	0.18	K0	NGC2264	Mathieu (1994)
LkCa31	12.94	0.20	M1	Tau-Aur	Mathieu (1994)
RX J1301.0-7654a2	13.1	0.06(?) $^{\dag\dag }$	K3+K4	Cha	Covino et al. (2001b, in prep.)
AKSco2	13.60	0.47	F5+F5	Sco-Cen	Andersen et al. (1989)
RX J1108.8-7519a2	13.75	0.47		Cha	Covino et al. (2001b, in prep.)
DQ Tau2	15.81	0.58	K4+K4	Tau-Aur	Mathieu et al. (1997)
155808-22191	16.93	0.10	M3	Sco-Cen	Mathieu (1994)
UZ Tau E	19.1	0.28		Tau-Aur	Mathieu et al. (1996)
P24942	19.48	0.26	K0	Trapezium	Reipurth et al. (2000)
P15402	33.73	0.12	K3+K5	Trapezium	Marschall & Mathieu (1988)
162814-24272	35.95	0.48	K2	$\rho$ Oph	Mathieu et al. (1989)
P19251	32.94	0.55	K3	Trapezium	Mathieu (1994)
RX J0530.7-04342	40.55	0.32	K2+K2	Orion	Covino et al. (2001a)
RX J0532.1-07322	46.87	0.48	K2+K3	Orion	Covino et al. (2001a)
V773 Tau2	51.08	0.27	K2+K5	Tau-Aur	Welty (1995)
Cru 32	58.28	0.06	K4+K5	Crux	Alcalá et al. (2001, in prep.)
162819-2423S1	89.1	0.41	G8	$\rho$ Oph	Mathieu et al. (1989)
160814-18571	144.7	0.26	K2	Sco-Cen	Mathieu et al. (1989)
P17711	149.5	0.57	K4	Trapezium	Mathieu (1994)
GWOri1	241.9	0.04	$^\dag$G5	B30	Mathieu et al. (1991)
HD 98800 A1	262.15	0.48	K5	Isolated	Torres et al. (1995)
HD 98800 B2	315.15	0.78	K5+K7	Isolated	Torres et al. (1995)
Haro1-14c1	590.78	0.62	K3	$\rho$ Oph	Reipurth et al. (2000)
VSB1111	879	0.8	G8	NGC2264	Mathieu (1994)
045251+30162	2517.77	0.47	K5+K7	Tau-Aur	Steffen et al. (2001)

$\parbox{18cm}{ $^1$\space Single-lined spectroscopic binary.\\ $^2$... ...whether the actual eccentricity is significant or not~$(e = 0.062\pm0.025)$ .}$

Figure 2: Orbital eccentricity versus orbital period for the PMS SB with known orbital elements. Circles stand for double-lined spectroscopic binary (SB2) systems and triangles stand for single-lined spectroscopic binary (SB1) systems. Those SB systems having one of the components clearly outside the range of mass explored by Zahn & Bouchet (1989) are shown as open symbols. The system RX J1301.0-7654a is indicated with an upper arrow since a non-zero eccentricity cannot be ruled out at the moment.

The main difference between our Fig. 2 and Fig. 2a of Mathieu (1994) is the addition of 13 new SB systems with $P_{\rm orb} < 100$ days and 2 systems with $P_{\rm orb} > 100$ days. The fact that the majority of the newly found systems are short-period, equal mass, and low to moderate eccentricity binaries can be understood as an observational bias since these systems are easier to be detected. Nevertheless, we can use these new short-period SB systems to revisit the important issue of the PMS circularization period.

The circularization period for a binary population is defined as the longest period for a circular orbit (Duquennoy et al. 1992). An inspection of Fig. 2 and/or of Table 3 indicates, therefore, that the PMS circularization period would now appear to be set by RX J1301.0-7654a ( $P_{\rm orb}=13.1$ days), assuming that its orbit is truly circular. The theory of the tidal interaction predicts that the synchronization between rotational and orbital motion is typically achieved more rapidly than orbital circularization ( $t_{\rm circ} \sim 10\times t_{\rm sync} \sim 10^6$ years) (e.g.: Zahn 1977; Zahn & Bouchet 1989). Thus, in theory we should expect that a binary system which was circularized by tidal interactions should be also synchronized. In order to check whether or not the rotation rate of both components of RX J1301.0-7654a is already synchronized with the orbital motion we need to estimate the radii for both components.

Covino et al. (2001b, in prep.) derived stellar parameters for both components of RX J1301.0-7654a using the matching technique described in Sect. 2.1. They obtained radii and ages of $R_{\rm a}=1.8\,R_\odot$ and $t_{\rm a}=2\times 10^6$ yr, and $R_{\rm b}=1.8\,R_\odot$ and $t_{\rm b}=2\times 10^6$ yr, for the primary and the secondary, respectively. Taking these values for the radii, we can now estimate the synchronous equatorial velocity for each component of RX J1301.0-7654a. Assuming $P_{\rm rot}=P_{\rm orb}=13.1$ days, we have ${\sim} 7$ km s^-1 for the synchronous equatorial velocity for both components. Comparing these values to the projected rotational velocities also given in Covino et al. (2001b) ($19\pm 1$ km s^-1for both components) we see that the components of RX J1301.0-7654a are rotating at least 2-3 times faster than the synchronous velocity. On this basis, we believe that RX J1301.0-7654a should not be used to define the PMS circularization period, at least until the issue is better understood and the circularity of the orbit confirmed.

 

 

Table 4: Circularization orbital period and age for non-evolved solar mass binaries.

Population	$P_{\rm circ}$	Reference	Age
	(days)	for $P_{\rm circ}$	(yr)
low-mass PMS	7.56	This paper	1- $10 \times 10^6$
Pleiades	7.05	MRDM92	$1.2 \times 10^8$
Hyades	8.50	GG	$6.25 \times 10^8$
Praesepe	8.00	MM99	$8 \times 10^8$
M 67	12.4	LMMD92	$5 \times 10^9$
Halo	18.7	L92	1- $1.5 \times 10^{10}$

GG - Griffin et al. (1985) and references therein;
Stefanik & Latham (1992).
LMMD92 - Latham et al. (1992).
L92 - Latham et al. (1992a).
MM99 - Mermilliod & Mayor (1999).
MRDM92 - Mermilliod et al. (1992).

The system with a circular orbit and the next highest period is RX J1603.9-3938 ( $P_{\rm orb} = 7.56$ days). The synchronous equatorial velocities for this binary computed from the radii given in Table 2 (${\sim}8.4$ km s^-1 and ${\sim}8.0$ km s^-1 for the primary and secondary, respectively) are higher than the projected rotational velocities, contrary to the case of RX J1301.0-7654a. Thus, synchronization cannot be ruled out in this case.

Although the hypothesis of synchronous rotation can only be confirmed if the angle i between the line of sight and the orbital plane is known, we can, nevertheless, try to test the plausibility of this hypothesis by using the theoretical masses inferred from the PMS tracks (given in Table 2), and the dynamical minimum masses obtained from the spectroscopic orbit. From the ratio between the theoretical and dynamical masses, for both components, it turns out that the inclination of the orbit should be around 38 degrees. If we assume that the spin axes are parallel to the axis of the orbit, then the expected projected rotational velocities are about 5 km s^-1 for both components, remarkably close to the measured $v\sin{i}$ values (6 and 5 km s^-1, respectively). Thus, despite the uncertainties involved in deriving the angle i from the comparison between dynamical and theoretical masses, such a test suggests that it is reasonable to assume that both components in RX J1603.9-3938 are rotating synchronously with the orbital motion. Because both synchronization and circularization seem to have been achieved in this system, we will assume here that RX J1603.9-3938 sets the new PMS circularization period at 7.56 days.

3.2 Are two different mechanisms really needed?

This new value of the circularization period for the PMS binaries is an important observational constraint supporting Zahn & Bouchet's (1989) idea that the quasi-totality of the orbital circularization occurs during the pre-main sequence phase, primarily near the stellar birth-line. According to their results, the circularization period set during the PMS phase for systems with masses ranging from 0.5 to 1.25 $M_{\odot}$ is about 7-8.5 days. In addition, as no further significant circularization occurs during the main-sequence phase, the circularization period for all binary populations (age < 10¹⁰ years) should be quite close to that established during the PMS phase.

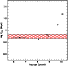Figure 3: Circularization orbital period as a function of age for the binary star populations listed in Table 4. The hatched area corresponds to the circularization orbital period interval predicted by Zahn & Bouchet (1989) as a result of the PMS tidal circularization. The error bars on the first and last points represent the age spread of the corresponding populations.

In Fig. 3, we show the circularization orbital period for the solar-mass binary populations listed in Table 4. The hatched area corresponds to the circularization orbital period interval predicted by Zahn & Bouchet (1989) as a result of the PMS tidal circularization. Despite the fact that the circularization periods observed for the PMS, Pleiades, Hyades and Praesepe binary populations agree with Zahn & Bouchet's (1989) prediction, the increase of the circularization period for older binary populations (M 67 and Halo stars) is also an observational constraint that cannot be neglected. Mathieu et al. (1992) suggest a hybrid scenario where PMS evolution could indeed establish a circularization period of 7-8.5 days which would be also observed for the binary population in young clusters and, after the lapse of about 10⁹ years, main-sequence tidal circularization would become effective. In fact, during the PMS phase the late-type stars have large radii and deep convective envelopes which allow the tidal-torque mechanism to be effective. Once the stars evolve towards the MS these conditions are not present anymore, as a consequence the tidal-torque mechanism looses its strength. Thus, a hybrid scenario requires the existence of a mechanism which will account for the circularization during the MS phase. Such a mechanism has been proposed by Tassoul (see references in Tassoul 1995 and Tassoul 2000), where the angular momentum exchanges are due to hydrodynamical motions (Tassoul 1987). He argues that both mechanisms can not only co-exist but also be complementary, as the hydrodynamical mechanism is quite ineffective during the contraction phase (PMS) and effective on the MS.

The Tassoul hydrodynamical mechanism has been strongly criticized in two papers by Rieutord (1992) and Rieutord & Zahn (1997) (see also Tassoul's reply in Tassoul & Tassoul 1997). These authors argue that Tassoul overestimated the strength of the Ekman pumping to spin-up (or spin-down) the fluid in the case where the container is not rigid but the gravitational potential of the star. The correct time-scale for the Ekman pumping to spin-up (or spin-down) the star would be much longer (Eq. (13) and examples in Sect. 4 in Rieutord & Zahn 1997). The theoretical debate behind the question of whether Tassoul's hydrodynamical mechanism actually operates is beyond the scope of this paper. Instead, let us recall that for the case of M 67 and Halo samples, the time-scales predicted by the tidal-torque mechanism and its variants (i.e., other developments than the original one by Zahn 1977) to circularize orbits up to the observed $P_{\rm circ}$ are, in both cases, much longer than the age of the sample (Mathieu & Mazeh 1988; Goldman & Mazeh 1991, 1992, see also Tassoul 1995, 2000; Goodman & Oh 1997). This fact does not necessarily lead to the rejection of the tidal-torque mechanism on the MS, it may only mean that future developments, regarding in particular the physical processes that transport angular momentum inside the stars, are needed to reconcile the tidal-torque mechanism with the observations.

Regardless the physics behind the circularization mechanism on the MS, the fact that the present data strongly support the hybrid scenario is an important result per se. As a main (qualitative) consequence of this observational result we can point out that at least up to a given time $t_{\rm MS}$ (which is of the order of the Hyades age accordingly to the present data), the circularization periods appear to be independent of the age of the samples, as opposed to increasing continuously as a function of time, as previously thought. Thus, they cannot be used either as a clock (Mathieu & Mazeh 1988) or to test different mechanisms and/or dissipation prescriptions against the data (Mathieu et al. 1992). Nevertheless, as a result of the MS tidal circularization, circularization periods start to increase again as a function of time for coeval samples older than $t_{\rm MS}$. Consequently, from this time until the moment in which the stellar structure (total mass, internal mass distribution, radii, etc.) can still be considered as constant (i.e., roughly until the end of MS), the circularization period-time relation can be used as a clock and to test different mechanisms and/or dissipation prescriptions for tidal effects.

3.3 The reliability of the data

The need for a hybrid scenario lies mainly on two observational facts, the increase of the circularization period for old binary populations and the PMS circularization period. Up to now, the main concern regarding the Zahn & Bouchet circularization scenario was the lack of observational support. Let us recall that the previous PMS orbital circularization period was set to 6.353 days by the system W134 found by Padgett & Stapelfeld (1994). However, the dynamical masses implied for this system are about $2~M_{\odot}$, thus suggesting that the mechanism proposed by Zahn & Bouchet does not have enough time to act due to the shortness of the fully convective phase in such massive stars (Padgett & Stapelfeld 1994). Thus, the discovery of RX J1603.9-3938 is an important observational constraint to the effectiveness of the PMS circularization which gives further support to Zahn and Bouchet's idea.

Due to its relevance, we will discuss the reliability of this PMS circularization period. We argued that, in spite of having circular orbit, the orbital period of the system RX J1301.0-7654a ( $e \approx 0$ and $P_{\rm orb}=13.1$ days) should not be taken as indicative of the PMS circularization period since neither component is synchronized. However, as the stars contract and the convection zone recedes, tidal braking loses its efficiency, and the conservation of angular momentum in the contracting stars leads to an increase of their rotational velocity which becomes greater than the orbital rate at the moment they arrive on the ZAMS (${\sim}$10⁷-10⁸ yrs). The ratio between rotational and orbital velocity will depend on the masses of the system (Zahn & Bouchet 1989). Afterwards, during the MS phase the rotation becomes synchronized again in less than one billion years, and no further significant decrease in the eccentricity occurs (Zahn & Bouchet 1989). Covino et al. (2001b) estimate the age of this system to be about ${\sim} 2\times 10^6$ yr. Thus, the system is still far from the ZAMS and, as a consequence, the argument given above cannot be used to explain its lack of synchronism. At about the age of RX J1301.0-7654a, however, Zahn & Bouchet (1989) predict that the rotational motion of the components of a binary system composed by two solar mass stars should already start to become unlocked with the orbital motion (see their Fig. 1). Even though, the lack of synchronism by a factor 2-3 observed in RX J1301.0-7654a is higher than that expected according Zahn & Bouchet scenario for a binary system (about 1.4).

Therefore, we consider the orbital period of the system RX J1603.9-3938, as being the one setting the PMS circularization period. We point out, however, that our decision to dismiss the apparently circular orbit of RX J1301.0-7654a as being a product of orbital circularization due to its lack of synchronism relies upon the theoretical work of Zahn & Bouchet (1989) which, in its turn, does not take into consideration disks, magnetic fields or mass accretion of the components which are important phenomena altering the angular momentum of both components of the system. Also, the determination of the circularization periods for the young binary populations listed in Table 4 usually relies on only one binary and the discovery of a new binary with a longer orbital period may change the circularization period of the population as was the case for the PMS SB population. The only effective way to overcome this difficult is to study large samples of binaries.

Another important point has to do with the direct comparison of the circularization period for different populations. In other words, are we comparing binary populations with a similar formation history, and if not, to what extent can the observed circularization periods be compared? In the tidal-torque mechanism the time-scale for the circularization will depend on the ratio (a/R)⁸, where a is the semi-major axis and R the stellar radius, on the parameter $\lambda_{\rm conv}$, which is related to depth of the convective zone (Zahn 1989), and on q, the mass ratio. Duchêne et al. (1998) have recently suggested that the binary frequency distribution as a function of the orbital period could depend on the initial conditions. Further supporting this, the results of Brandner & Köhler (1998) seem to indicate that even the shape of the distribution could depend on the physical properties of the parental cloud. Therefore, it seems that the initial distribution of semi-major axes depends on the environment. This leads to the possibility that some binary populations may be born with larger fractions of very close systems (say, $P_{\rm orb} \le 15$ days) compared to other populations. In that case, because of the denser sampling of orbital periods near the critical value, the observed circularization period would tend to be longer than in populations with few binaries in this regime. At the moment, based on the existing data for main sequence binaries in the solar neighborhood (Duquennoy & Mayor 1991) and for PMS binaries (Mathieu et al. 1992) in the range of separation corresponding to $P_{\rm orb} < 100$ days, the evidence indicates a very similar fraction of spectroscopic binaries of about 10% in both samples. Thus, it seems unlikely that a given binary population has a longer circularization period due to the fact that more short-period binaries were initially formed.

The other parameters (R, $\lambda_{\rm conv}$) are related to the stellar mass. Zahn & Bouchet (1989) tested the sensitivity of $P_{\rm circ}$ to the stellar mass and mass ratio. They predict that a little increase of $P_{\rm circ}$ with mass and with mass ratio should occur ( $P_{\rm circ}$ ranging from 7.28 up to 8.54 days). Zahn & Bouchet also noted that, if the circularization period as a function of the mass is known, we could in principle constrain both the accretion rate and deuterium abundance since the mass-radius relation given by Stahler (1988) depends on these quantities and so does $P_{\rm circ}$. Nevertheless, at least in a first moment, this spread in $P_{\rm circ}$ due to the stellar mass can be neglected since not enough data are available to allow to determine $P_{\rm circ}$ per mass bin.

As a last important point, from Table 3 we note the existence of three systems with orbital periods shorter than the new circularization period of 7.56 and still having an eccentric orbit. According to Zahn & Bouchet (1989) such systems should not exist since the tidal circularization occurring near the birthline would be strong enough to circularize their orbits. Why are these orbits still eccentric? The answer is not actually known. One possibility to explain the eccentric orbits of these short-period systems might be the pertubations caused by a small mass companion (e.g., Mazeh 1990) or induced by the presence of disks (e.g., Lubow & Artymowicz 1992). Regarding this later possibility, Artymowicz et al. (1991) studied how a circumbinary disk changes the orbital elements of a central binary system. Their main result is that in general the semi-major axis decreases and the eccentricity of the binary is forced to grow. Lubow & Artymowicz (1992) reinvestigated the problem and concluded that for binaries with small initial eccentricities (e<0.2), the eccentricity will rapidly grow, while for binaries with initial higher eccentricities (e>0.5) the outcome will depend on other parameters of the problem. This means that a PMS binary system possessing a disk of about 1% of the total mass of the central binary will start to experience the effects of pure tidal circularization (i.e., without competing effects that will tend to increase eccentricity) only after the dissipation of its disk. As a consequence, binaries that preserve their disk for long time-scales (say 1-10 $\times 10^6$ years) will probably arrive on the ZAMS with high eccentricities as they do not have enough time to circularize their orbits. Among the four confirmed CTTS, three of them, DQ Tau, AK Sco and UZ Tau E, have short-period $P_{\rm orb}<20$ days and moderate eccentricities while the other, GW Ori has a period of 241.9 days and eccentricity less than 0.1! Clearly, more observational effort must be made in finding more PMS spectroscopic binaries of both types (WTTS and CTTS) which will enable us to have an $e-\log P$ diagram for each type. In addition, surveys devoted to derive disk properties like the mass distribution profile and accretion behavior (e.g., Jensen & Mathieu 1997; Duchêne et al. 1999; McCabe & Ghez 2000) will provide important observational constraints to better understand the orbital evolution in a circumbinary and/or circumstellar environment.