

Up: On the pre-main sequence period
Subsections
In Table 1 we present radial velocity observations for the double-lined
spectroscopic binary RX J1603.9-3938![[*]](/icons/foot_motif.gif) carried out with the
spectrograph CORALIE attached to the Swiss Euler Telescope at ESO, La Silla. The radial velocity curve is shown
in Fig. 1 and the respective orbital elements and stellar parameters for both
components are given in Table 2. The system has a circular orbit and an orbital
period of 7.56 days. Its barycentric velocity (
carried out with the
spectrograph CORALIE attached to the Swiss Euler Telescope at ESO, La Silla. The radial velocity curve is shown
in Fig. 1 and the respective orbital elements and stellar parameters for both
components are given in Table 2. The system has a circular orbit and an orbital
period of 7.56 days. Its barycentric velocity (
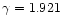 km s-1) is in agreement with
the mean radial velocity (
km s-1) is in agreement with
the mean radial velocity (
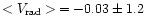 km s-1) of the 9 Lupus bona-fide CTTS and
with the mean radial velocity (
km s-1) of the 9 Lupus bona-fide CTTS and
with the mean radial velocity (
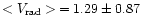 km s-1) of the "on-cloud'' Lupus ROSAT WTTS both
listed in Wichmann et al. (1999).
km s-1) of the "on-cloud'' Lupus ROSAT WTTS both
listed in Wichmann et al. (1999).
Determination of luminosities and spectral types were
obtained for both components through a matching of the binary spectrum with that of a synthetic binary
following the prescription of Lee et al. (1994). Details on the application of the matching
technique and on the radial and rotational velocities determination
are given in Covino et al. (2000, 2001a). Once individual luminosities have been derived, we can
estimate the true Li I 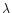 6708 Å equivalent width for each component (i.e. the equivalent width
corrected from the veiling due to continuum of the companion). The values given in Table 2 show that the Li I
content in both components of RX J1603.9-3938 are higher than those observed in stars of same spectral type
at the age of Pleiades (
6708 Å equivalent width for each component (i.e. the equivalent width
corrected from the veiling due to continuum of the companion). The values given in Table 2 show that the Li I
content in both components of RX J1603.9-3938 are higher than those observed in stars of same spectral type
at the age of Pleiades (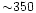 mÅ for K2 and
mÅ for K2 and 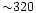 mÅ for a K4).
Finally, ages, masses and the radii for both
components were determined from evolutionary models by
D'Antona & Mazzitelli (1997). The choice of using the
evolutionary models by D'Antona & Mazzitelli to derive ages and radii is completely arbitrary
since there is no standard PMS evolutionary model. The reader should be aware that other models can
yield different masses and ages (e.g., Baraffe et al. 1998; see e.g.,
Simon et al. 2000; Covino et al. 2001a
for a comparison between
different evolutionary tracks). However, we stress that the use of other sets
of PMS tracks does not change the main conclusions of this paper.
Together, the Li content of each component, the barycentric velocity of the system and its age strongly suggest that both components of RX J1603.9-3938 are in fact bona-fide T-Tauri stars.
mÅ for a K4).
Finally, ages, masses and the radii for both
components were determined from evolutionary models by
D'Antona & Mazzitelli (1997). The choice of using the
evolutionary models by D'Antona & Mazzitelli to derive ages and radii is completely arbitrary
since there is no standard PMS evolutionary model. The reader should be aware that other models can
yield different masses and ages (e.g., Baraffe et al. 1998; see e.g.,
Simon et al. 2000; Covino et al. 2001a
for a comparison between
different evolutionary tracks). However, we stress that the use of other sets
of PMS tracks does not change the main conclusions of this paper.
Together, the Li content of each component, the barycentric velocity of the system and its age strongly suggest that both components of RX J1603.9-3938 are in fact bona-fide T-Tauri stars.
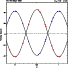 |
Figure 1:
Radial velocity curve of RX J1603.9-3938. Radial velocities observations for the
primary and secondary components are drawn as a filled and open circles, respectively. |
The orbital period and eccentricity for the PMS binary systems known to the
authors are listed in Table 3. When available in respective reference,
the spectral type of the components is
given. When only the effective temperature is available we use the calibration
of de Jager & Nieuwenhuijzen (1987) to transform effective temperatures into spectral types.
We also mark the systems in which at least one of the components is not within the
mass range investigated in Zahn & Bouchet (1989). The nature of the spectroscopic binary
system (i.e., single- or double-lined) is indicated as well.
Comparing our Table 3 to Mathieu's (1994) Tables A1 and A2, we
list 15 new entries.
Also, some entries listed in Mathieu (1994) had their reference updated, but
a few of them still remain unpublished. In Table 4 we list age and
circularization period with their respective references for other low-mass binary
populations for which the circularization period is determined.


Up: On the pre-main sequence period
Copyright ESO 2001
