To study the problem of linear conversion of waves it is necessary to
specify the location of the region of quasi-longitudinal propagation.
Ray propagation in the magnetosphere is generally quasi-transverse. Given that
a ray is emitted tangentially to the field line of a dipolar magnetic field
and propagates along a straight line, the tilt of the wave vector to the ambient
magnetic field increases monotonically along the trajectory due to magnetic
line curvature. However, refraction of waves in pulsar plasma can be significant
(Barnard & Arons 1986; Lyubarskii & Petrova 1998), so that both the wave
vector direction and the ray trajectory can be considerably modified.
Since the plasma number density decreases rapidly along the ray trajectory,
refraction appears to cease at distances
![]() ;
further on the rays follow
a straight line and can pass through the region where they are almost aligned with
the ambient magnetic field.
;
further on the rays follow
a straight line and can pass through the region where they are almost aligned with
the ambient magnetic field.
Given that the rays
propagate in the plane of magnetic lines (the xz-plane), it is not
difficult to find that after refraction the polar angle of the ray
trajectory, ![]() ,
is given by the expression:
,
is given by the expression:
| (13) |
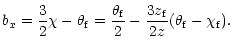 |
(14) |
| (15) |
Figure 1 shows the location of the region of quasi-longitudinal propagation,
![]() ,
for the rays with different final tilts to the magnetic axis (in the case
of the central cut of the emission cone by the sight line,
,
for the rays with different final tilts to the magnetic axis (in the case
of the central cut of the emission cone by the sight line,
![]() corresponds to pulse longitude) at two different frequencies.
The data presented in this figure are obtained
through numerical solution of ray equations in pulsar plasma (Eq. (9) in Petrova
2000). The distribution of the plasma number density across the open field
line tube is taken in the form of two Gaussians centred on the
characteristic field lines symmetrically with respect to the magnetic axis.
Because of the symmetry of the problem only one half of the pulse profile is
plotted.
corresponds to pulse longitude) at two different frequencies.
The data presented in this figure are obtained
through numerical solution of ray equations in pulsar plasma (Eq. (9) in Petrova
2000). The distribution of the plasma number density across the open field
line tube is taken in the form of two Gaussians centred on the
characteristic field lines symmetrically with respect to the magnetic axis.
Because of the symmetry of the problem only one half of the pulse profile is
plotted.
As is evident from Fig. 1, the regime of quasi-longitudinal propagation is
characteristic of a number of rays (both inner and outer). Note that for both
frequencies the same number of initially equidistant rays was considered.
One can see that in Fig. 1 the rays at the higher frequency (points) are more
numerous than those at the lower frequencies (asterisks). So at higher frequencies,
where refraction is more efficient, the quasi-longitudinal regime holds for the
larger part of the pulse. For most of the rays
![]() ,
i.e. the region of
interest lies not too high in the magnetosphere.
,
i.e. the region of
interest lies not too high in the magnetosphere.
One more marked feature can be observed in Fig. 1: for the high-frequency inner
rays the curve is double-valued. The point is that due to refraction two rays
emitted at different angles to the magnetic axis can have the same final tilts,
whereas their trajectories are different (for more details see, e.g., Petrova
2000), so that at a given pulse longitude one can observe the rays coming
from different locations in the magnetosphere. Each of these rays passes only once
through the region of quasi-longitudinal propagation (for the two rays at a fixed
pulse longitude ![]() has distinct values).
has distinct values).
It should be mentioned that in the present consideration we concentrate
on the qualitative features of ray behaviour on account of refraction which make
possible the regime of quasi-longitudinal propagation. The quantitative results
depend on the concrete form of the assumed plasma density distribution.
For that reason we do not give the numerical values of ray frequencies in Fig. 1
(the frequency ratio is derived from the ratio of the emission altitudes
on the basis of radius-to-frequency mapping,
![]() ).
Note that at a fixed frequency the observed profile widths and shapes are
known to be quite distinct for different pulsars; this hints at an actual variety
in the parameters of pulsar plasma.
).
Note that at a fixed frequency the observed profile widths and shapes are
known to be quite distinct for different pulsars; this hints at an actual variety
in the parameters of pulsar plasma.
Recall that above we have considered ray propagation in the plane of magnetic
lines.
In reality the waves can slightly bend from this plane either because of refraction in the plasma with a
non-axisymmetric density distribution or because of the magnetosphere rotation.
So in general by is not equal to zero, though far enough from ![]() ,
it
is much less than bx (for numerical estimates see Sect. 3.6).
,
it
is much less than bx (for numerical estimates see Sect. 3.6).
Now let us turn to linear conversion of waves.
For the sake of clarity we start from the case of an infinitely
strong magnetic field. Then the set of Eqs. (12) is reduced
to the form:
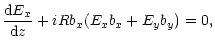 |
|||
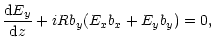 |
(16) |
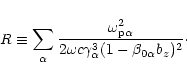
| (17) |
![$\displaystyle \frac{b_x}{\sqrt{b_x^2+b_y^2}}\exp \left[-i\int R(b_x^2+b_y^2){\rm d}z\right],$](/articles/aa/full/2001/42/aa1063/img101.gif) |
|
![$\displaystyle \frac{b_y}{\sqrt{b_x^2+b_y^2}}\exp \left[-i\int R(b_x^2+b_y^2){\rm d}z\right],$](/articles/aa/full/2001/42/aa1063/img103.gif) |
|
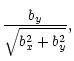 |
|
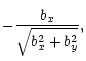 |
(18) |
In a narrow region close to ![]() both bx and by are so small that the
approximation of geometrical optics is broken. On both sides out of this
region the solution of Eq. (13) is the linear combination of the natural waves
(Eq. (15)), with the coefficients at
both bx and by are so small that the
approximation of geometrical optics is broken. On both sides out of this
region the solution of Eq. (13) is the linear combination of the natural waves
(Eq. (15)), with the coefficients at
![]() and
and
![]() being distinct.
For example, if at
being distinct.
For example, if at
![]() we have only the ordinary wave, at
we have only the ordinary wave, at
![]() both
natural waves arise.
both
natural waves arise.
To find the intensity ratio of the outgoing waves it is necessary
to obtain the exact solution of Eq. (13) in the region of
conversion. Note that in this case we can use the
quasi-homogeneous approximation: within the narrow region of
interest,
![]() ,
one can present bxin the form:
,
one can present bxin the form:
![]() ,
where
,
where
![]() ,
while all
the other quantities have approximately the same values as at
,
while all
the other quantities have approximately the same values as at
![]() .
Hence, for the region of conversion the set of
Eq. (13) is written as
.
Hence, for the region of conversion the set of
Eq. (13) is written as
| (19) |
Despite the considerable simplification provided by the quasi-homogeneous approximation, the set of Eq. (19) remains too complicated: its exact solution cannot be expressed via the known functions. Note that in contrast to the above situation, the problem of linear conversion in a non-relativistic, weakly magnetized plasma allows an exact analytical solution (it is expressed via the functions of a parabolic cylinder) and it is well studied in application to solar plasma (see, e.g., Zhelezniakov 1996 and references therein).
Let us assume that ![]() .
Then the solution of Eq. (19) can be
found by means of successive approximations. Presenting the wave
amplitudes in the form
.
Then the solution of Eq. (19) can be
found by means of successive approximations. Presenting the wave
amplitudes in the form
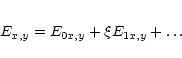
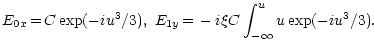 |
(20) |
| (21) |
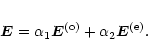
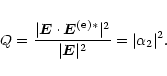
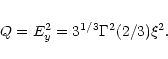
The coefficient of conversion calculated numerically as a function of ![]() is plotted in Fig. 2. One can see that the conversion is significant for
is plotted in Fig. 2. One can see that the conversion is significant for
![]() .
It should be pointed out that the physical meaning of the parameter
.
It should be pointed out that the physical meaning of the parameter
![]() is the phase difference of the natural modes acquired during their
passing through the region of conversion. Indeed, the characteristic length
of the region of conversion is
is the phase difference of the natural modes acquired during their
passing through the region of conversion. Indeed, the characteristic length
of the region of conversion is
![]() ,
i.e.
,
i.e.
![]() .
Taking into account that the
difference of the refractive indices is
.
Taking into account that the
difference of the refractive indices is
![]() ,
we find:
,
we find:
![]() .
.
![\begin{figure}\includegraphics[width=8.8cm,clip]{M1063F2.EPS}\end{figure}](/articles/aa/full/2001/42/aa1063/Timg149.gif) |
Figure 2:
The degree of mode conversion, Q, as a function of mode
phase difference, |
As is clear from Fig. 2, Q does not exceed 0.5. Hence, if the approximation of an infinitely strong magnetic field is the case, the extraordinary mode never dominates over the ordinary one, though the intensities can be comparable and, correspondingly, the outgoing radiation can be strongly depolarized.
Let us turn to the opposite limiting case: by=0, whereas B0 is finite
and ![]() .
Then the set of Eq. (12) is written as
.
Then the set of Eq. (12) is written as
| (22) |
![$\displaystyle \frac{i(b_x^2/2+\sqrt{b_x^4/4+g^2})}{\sqrt{g^2+[b_x^2/2+
\sqrt{b_x^4/4+g^2}]^2}}$](/articles/aa/full/2001/42/aa1063/img157.gif) |
|
![$\displaystyle \times\exp \left[-i\int R(b_x^2/2+\sqrt{b_x^4/4+g^2}){\rm d}z\right],$](/articles/aa/full/2001/42/aa1063/img158.gif) |
|
![$\displaystyle \frac{g}{\sqrt{g^2+[b_x^2/2+
\sqrt{b_x^4/4+g^2}]^2}}$](/articles/aa/full/2001/42/aa1063/img160.gif) |
|
![$\displaystyle \times\exp \left[-i\int R(b_x^2/2+\sqrt{b_x^4/4+g^2}){\rm d}z\right],$](/articles/aa/full/2001/42/aa1063/img158.gif) |
|
![$\displaystyle \frac{i(b_x^2/2-\sqrt{b_x^4/4+g^2})}{\sqrt{g^2+[b_x^2/2-
\sqrt{b_x^4/4+g^2}]^2}}$](/articles/aa/full/2001/42/aa1063/img162.gif) |
|
![$\displaystyle \times\exp \left[-i\int R(b_x^2/2-\sqrt{b_x^4/4+g^2}){\rm d}z\right],$](/articles/aa/full/2001/42/aa1063/img163.gif) |
|
![$\displaystyle \frac{g}{\sqrt{g^2+[b_x^2/2-
\sqrt{b_x^4/4+g^2}]^2}}$](/articles/aa/full/2001/42/aa1063/img165.gif) |
|
![$\displaystyle \times\exp \left[-i\int R(b_x^2/2-\sqrt{b_x^4/4+g^2}){\rm d}z\right].$](/articles/aa/full/2001/42/aa1063/img166.gif) |
(23) |
In the region
![]() Eq. (22) can be
treated in the quasi-homogeneous approximation. So we obtain:
Eq. (22) can be
treated in the quasi-homogeneous approximation. So we obtain:
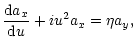 |
|||
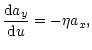 |
(24) |
![\begin{figure}\par\includegraphics[width=8.8cm,clip]{M1063F3.EPS}\end{figure}](/articles/aa/full/2001/42/aa1063/Timg175.gif) |
Figure 3:
The degree of mode conversion, Q, as a function of mode
phase difference, |
The above results pose the question of whether the conversion is efficient
at
![]() ,
i.e. given that both by and g cannot be neglected. In
the geometrical optics approximation the solutions of Eq. (12) are as
follows:
,
i.e. given that both by and g cannot be neglected. In
the geometrical optics approximation the solutions of Eq. (12) are as
follows:
ax=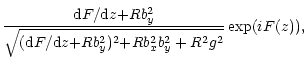 |
|
ay=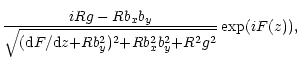 |
(25) |
The quasi-homogeneous problem is reduced to the form:
| (26) |
After leaving the region of conversion the waves propagate independently
until the geometrical optics approximation is violated. The plasma number
density decreases along the trajectory and the waves tend to become the
vacuum electromagnetic ones. As soon as the difference in the refractive
indices becomes so small that the scale length for beatings between the
natural waves becomes comparable to the scale length for change in the
plasma parameters,
| (27) |
It should be noted that the consequences of the mode coupling are
essentially distinct from the linear conversion studied above.
The problem is that in the region of conversion Eq. (27) is
satisfied twice: at first ![]() decreases strongly because
decreases strongly because
![]() and then it increases up to its initial value. As
and then it increases up to its initial value. As
![]() the incident ordinary wave suffers the
polarization changes similar to those resulting from the
polarization-limiting effect. Later on, as
the incident ordinary wave suffers the
polarization changes similar to those resulting from the
polarization-limiting effect. Later on, as ![]() starts
increasing, this modified wave is split into two natural waves.
starts
increasing, this modified wave is split into two natural waves.
The polarization-limiting effect has been already studied in detail in
application to the ordinary waves (Petrova & Lyubarskii 2000). It was found
that a number of features of the observed polarization profiles can be
attributed to this effect. Now we turn to it once more in order to compare
the evolution of both orthogonal modes. Let us assume that the plasma
number density decreases as z-3 and
![]() ,
,
![]() .
Although this model is somewhat abstract, it appears to be sufficient to
clarify the qualitative picture of the polarization-limiting effect for
both natural modes.
.
Although this model is somewhat abstract, it appears to be sufficient to
clarify the qualitative picture of the polarization-limiting effect for
both natural modes.
As was already discussed at the beginning of Sect. 2, far from the
region of conversion the approximation of an infinitely strong
magnetic field is appropriate. Then the set of Eqs. (12) can
be presented in the form:
| (28) |
![\begin{eqnarray*}&&R(z_{\rm p})[b_x^2+b_y^2(z_{\rm p})]z_{\rm p}=1, \\
&&\mu\eq...
...)_{z=z_{\rm p}},\ s(w)\equiv\frac{1+\mu^2}{(1+\mu^2/w^2)^2}\cdot
\end{eqnarray*}](/articles/aa/full/2001/42/aa1063/img198.gif)
Now let us turn to the numerical results on the final polarization state of
the waves escaping from the plasma. The degree of circular polarization is
characterized by the normalized Stokes parameter V:
V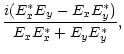 |
(29) |
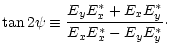 |
(30) |
As is found in the previous subsections, the linear conversion is governed
by the parameters ![]() and
and ![]() ,
while the polarization-limiting effect is
determined by
,
while the polarization-limiting effect is
determined by ![]() .
Now we proceed to the numerical estimates of these
parameters in application to typical pulsar conditions.
.
Now we proceed to the numerical estimates of these
parameters in application to typical pulsar conditions.
Although R is the sum over the particle species, it is clear
that either one of the addends contributes chiefly or both
contributions are nearly equal. So for our estimates one can
write:
![]() ;
here it is taken into
account that in the region of conversion
;
here it is taken into
account that in the region of conversion
![]() and
and
![]() .
The waves are supposed to originate
at the characteristic plasma frequency, i.e. at the emission
origin
.
The waves are supposed to originate
at the characteristic plasma frequency, i.e. at the emission
origin
![]() ,
and
further along the trajectory the plasma number density, N,
decreases as z-3, so that
,
and
further along the trajectory the plasma number density, N,
decreases as z-3, so that
![]() .
Assuming that
.
Assuming that
![]() with
with
![]() one can obtain:
one can obtain:
| (31) |
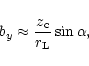
| (32) |
Note that in contrast to R the expression for G contains the difference of
the contributions of electrons and positrons. Therefore one can write:
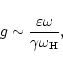
| (33) |
The result of the polarization-limiting effect is determined by the parameter
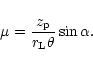
Copyright ESO 2001